2.2 Расчет расширенных афх фчх объекта для заданного запаса устойчивости

(4)

АФХ объекта

тогда

(5)

Подставим в формулу вместо

Преобразуем числитель:

(6)

Из формулы (6) выделяем вещественную часть – P(m,ω) и коэффициент при мнимой части Q(m,ω)

(7)

Находим АЧХ объекта:

Подставляем в выражение для А_об(m,ω):

Подставляя вместо a и b их выражения получим:

(8)

Находим ФЧХ объекта:

Для нахождения отношения , воспользуемся выражением (5):

P(m,ω) -jQ(m,ω)

тогда

(9)

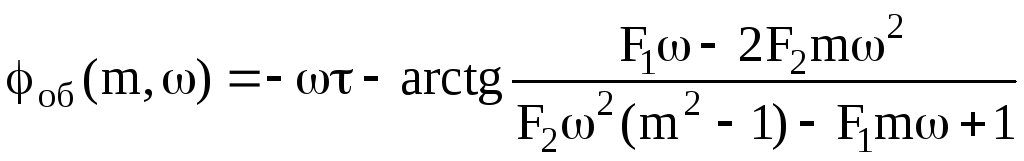
Находим численные значения для расширенных характеристик объекта:

F₁ = 25,32; F₂ = 156,54; K_об = 1,75; τ = 6; m = 0,302 (из пункта 1)

Для построения графиков А_об(m,ω) и φ_об(m,ω) используется участок АФХ в области рабочих частот.

3. Определение оптимальных настроечных параметров регулятора

Строим линию равного затухания переходного процесса в плоскости настроечных параметров. Для расчета используется формула (8) – выражение для и

(9) – выражение для .ипредставляются табличной форме. Расчет выполняется в программеRcho.exe(X = ω, F = φ, ω = [0,00÷0,22] – 15 точек), результаты расчета приведены в приложении Г.

П

(10)

ередаточная функция П-И – регулятора

K_R – коэффициент передачи пропорциональной части

- коэффициент передачи интегральной части

- время интегрирования

Расчетные формулы для K_R и :

(11)

(12)

Придавая ω ряд значений ([0,00÷0,22] – 15 точек) по формулам (11) и (12) находим значения K_R и и строим график по программеLinz.exe, где Q[i] = ,K[i] = K_R и X[i] = ω, i – номер точки (приложение Д).

Из графика определяем оптимальные значения параметра. Условием оптимальности является минимум интегрального критерия качества, который обеспечивается при =max.

K_R = 0,70358

(13)

- степень упругой связи

(14)

(15)

-показатель затухания регулятора

3. Определение запаса устойчивости сар по модулю (%) и по фазе (°с)

Используя критерий Найквиста, находим АФХ разомкнутой системы с П-И регулятором.

П

(16)

ередаточная функция разомкнутой системы.

W_раз (Р) = W_об (Р)  W_R (P)

Подставляя в формулу (16) вместо W_об (Р) выражение (4), а вместо W_R (P) выражение (10) и проведя преобразования получим:

(17)

Найдем выражение для АФХ разомкнутой системы без запаздывания. Для этого в формуле (17) без сомножителя ^-р заменим р на j, получим:

АФХ разомкнутой системы с запаздыванием

Вывод

В результате расчета найдены следующие настройки П-И регулятора:

K_R = 0,70358

- степень упругой связи

Система устойчива с запасом

По модулю с = 0,58 (определяется из графика в приложении Е)

По фазе γ = 48,3° (определяется из графика в приложении Е)

3. Определение прямых оценок качества регулирования при

единичном задающем воздействии

1. Определяем передаточную функцию замкнутой системы по задающему воздействию

(18)

Подставляя значения в выражение (18) получаем:

2. Определение вещественной частотной характеристики замкнутой системы

В выражении (18) заменим :

(19)

Выделяем из выражения (19) вещественную часть Р(ω):

(20)

Подставляя в выражение (20) численные значения и проведя преобразования, получим:

(21)

Значения вещественной частотной характеристики рассчитываются в программе Gchх.3401.exe (приложение Ж).

3. Расчет и построение переходного процесса методом трапецеидальных частотных характеристик.

   1. Кривая ВЧХ заменяется ломаной линией (касательными к каждой точке сопряжения). Ломаная линия заменяется трапециями так, чтобы площадь, ограниченная ломаной линией, была точно равна сумме всех трапеций, взятых с соответствующим знаком. Трапеции обязательно должны начинаться от точки ω = 0 (одна боковая грань лежит на оси ординат), а основание должно быть параллельно оси абсцисс. Приложение З.

   2. Для каждой определенной трапеции рассчитывается соответствующий переходный процесс и строится график переходного процесса. Графически складываясь, ординаты переходных процессов образуют переходный процесс системы в целом (приложение К).

r_о –высота;

ω₀ - частота, при которой заканчивается верхнее основание трапеции;

₁ –частота, при которой заканчивается нижнее основание трапеции;

- наклон трапеции.

Первая трапеция

ω₀ = 0,05 ω₁ = 0,09 = 0,55 r₀ = 2,1;

Вторая трапеция

ω₀ = 0,09 ω₁ = 0,15 = 0,6 r₀ = -0,71;

Третья трапеция

ω₀ = 0,15 ω₁ = 0,19 = 0,8r₀ = -0,22;

Четвертая трапеция

ω₀ = 0,19 ω₁ = 0,3 = 0,65 r₀ = -0,16;

По формулам

находятся действительное время Т_д и амплитуда Y для каждой трапеции переходного процесса системы в целом (приложение И).