Часть 2. Фазовые превращения в конденсированных средах (жидкое и твердое состояние)
2.1. Зарождение (гомогенное и гетерогенное) частиц новой фазы в сплавах;
В физике фазовых превращений в сплавах принято, в соответствии с теорией Гиббса, что зарождение частиц новой фазы происходит за счет результирующего уменьшения свободной энергии системы при наличии соответствующих флуктуаций.
Гиббс проводит следующее различие между двумя типами флуктуаций:
-
представляющих значительные перегруппировки атомов в небольших объемах;
-
переставляющих незначительные перегруппировки атомов в больших объемах;
Обычно зарождение новой фазы начинается с образования физически различимых центров, после чего претерпевшие превращение данные области растут в окружающую их среду.
Таким образом, данный процесс в определенном смысле является гетерогенным, так как во время превращения в системе появляются новые поверхности (межфазные границы). Вместе с тем, в соответствии с теорией фазовых превращений данный процесс относится к гомогенному зарождению.
Гетерогенное зарождение реализуется при зарождении частиц новой фазы в определенных локальных местах структуры матричной фазы, характеризующихся повышенным (относительно среднего) уровнем свободной энергии.
В классической теории фазовых превращений образование зародышей обычно рассматривается в ракурсе флуктуаций первого типа, то есть любая система в достаточно малом объеме будет находиться в устойчивом состоянии относительно таких флуктуаций.
Это связано с тем, что при фазовых превращениях отрицательному по знаку изменению свободной энергии, обусловленному образованием некоторого объема более стабильной фазы, противостоит положительное по знаку изменение свободной энергии, связанное с появлением межфазной границы.
Рассмотрим в качестве примера следующий простой случай (полиморфное превращение):
Бинарный сплав (состава С = С1) охлажден (рис.8) с температуры Т0 (однофазная область - а - фаза) до температуры Т1 (однофазная область - в - фаза), то есть при образовании зародыша новой фазы в данном случае не происходит изменение концентрации в области превращения, а только перестраивается кристаллическая решетка матричной фазы.
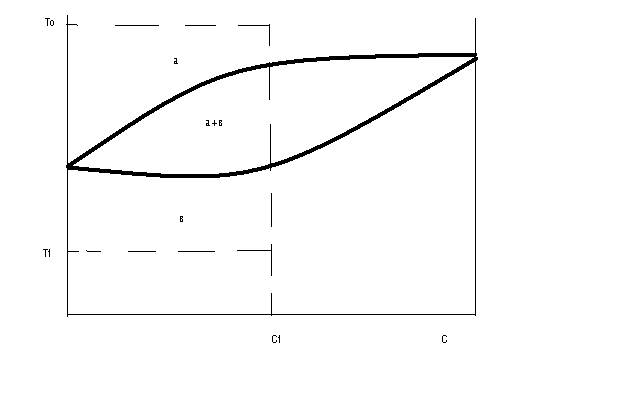
Рис.8. Диаграмма состояния (схема).
При образовании сферического зародыша в- фазы выражение для свободной энергии системы будет иметь следующий вид:
G = n (μв - μа) + σ S + n ∆gs,
где n - число атомов в зародыше;
μв - μа - химические потенциалы компонента в фазах в и а ;
n∆gs - результирующая энергия, связанная с возникновением упругой деформации;
σ - коэффициент поверхностного натяжения;
S - площадь поверхности зародыша.
Учитывая, что
n = Vз/Vaт = 4 (π R³)/3 Vaт, S= 4πR²
(Vз - объем зародыша, Vaт - средний объем атома)
G(R) = 4π R³ (μв - μа + ∆gs)/ 3Vaт + 4π σ R²
Данная зависимость G(R) будет иметь максимум в точке R=Rk (критический радиус зародыша)
Rk = - 2σ Vaт/(μв - μа + ∆gs) = 2σ Vaт/gэф,
где gэф = - (μв - μа + ∆gs) = (μа - μв - ∆gs) – эффективная движущая сила.
Поскольку для реализации процесса фазового превращения эффективная движущая сила должна иметь положительное значение, то
μа > μв+ ∆gs.
В соответствии с зависимостью функции G(R) от радиуса образующейся частицы новой фазы, точка R=Rk является координатой неустойчивого равновесия зародыша:
при R < Rk - зародыш растворяется;
при R > Rk - зародыш растет.
Причем величина критического радиуса зародышей смещается в сторону больших значений при увеличении коэффициента поверхностного натяжения σ и уменьшении эффективной движущей силы gэф.
Это очень существенный момент, поскольку величина критического радиуса определяет, согласно теории Бекера – Деринга, стационарную скорость (или вероятность) образования зародышей
Iv ~ exp -λ (R k)²/кT (λ – коэффициент),
которая уменьшается по мере возрастания Rk.
В свою очередь, величина σ и ∆gs (соответственно и в целом gэф) в значительной степени зависит от класса межфазной границы, что связано с соответствием сопряжения кристаллической решетки матричной фазы с кристаллической решеткой образовавшейся фазы.
Межфазные границы делятся на три основных класса: когерентные, полукогерентные, некогерентные.
Когерентными считаются границы, когда плоскость раздела фаз является общей для их решеток. В общем случае, когда неточность сопряжения решеток соприкасающихся фаз невелика, когерентность обеспечивается за счет упругой деформации.
Полукогерентными считаются межфазные границы (сопоставимые с малоугловой границей зерна), на отдельных участках которой в результате упругой деформации наблюдается когерентность, на других же участках постепенно накапливается несоответствие, которое периодически устраняется за счет возникновения разрыва.
Некогерентным считаются межфазные границы, имеющие сильное разупорядочение (сопоставимо с большеугловой границей зерна).
Таким образом, в случае образования когерентных зародышей, коэффициент поверхностного натяжения мал, а упругая энергия, наоборот, велика.
Некогерентные зародыши имеют значительно большую величину коэффициента поверхностного натяжения, но меньшую упругую энергию.
В случае, когда в системе образуются зародыши химического соединения (карбиды, нитриды, интерметаллиды и т.п.) зависимость стационарной скорости образования зародышей от критического радиуса, полученная Бекером – Дерингом, сохраняется.
Равновесное состояние между твердым раствором (например, некой γ-фазой) и химическим соединением AmBn, образованным в соответствии с реакцией
mA + nB=AmBn
описывается следующим выражением, являющимся уравнением линии растворимости, которая ограничивает двухфазную область (γ + AmBn):
m ln(aA)р + n ln(aB)р = ∆GAmBn ,
где (aA)р и (aB)р – термодинамические активности компонентов А и В в твердом растворе в условиях равновесия с соединением AmBn;
∆GAmBn – свободная энергия образования соединения AmBn.
При этом следует отметить, что хотя зависимость критического размера зародыша соединения от эффективной движущейся силы сохраняет тот же вид
Rk = 2σVм/gэф (Vм - объем молекулы),
но эффективной движущей силой gэф в данном случае будет наличие пересыщения твердого раствора, поскольку в твердом растворе концентрация компонента А, сразу после охлаждения γ-фазы из однофазной области до температуры существования двухфазной области, больше своего равновесного значения и с данного момента времени начинается процесс образования новой фазы:
gэф = кТ[m ln(aA) + n ln(aB) - m ln(aA)р + n ln(aB)р - ∆gs/кТ] =
кТ[m ln(aA) + n ln(aB) - (∆GAmBn + ∆gs)/кТ],
где [m ln(aA) + n ln(aB)] – текущее «произведение активности» компонентов А и В в твердом растворе в условиях формирования зародышей химического соединения и соответственно двухфазной области соответствует началу процесса образования.
Из анализа данного выражения для эффективной движущей силы, следует, подобному ранее приведенному, что критический радиус зародыша имеет положительное значение (Rk > 0) при условии gэф>0, которое выполняется, когда
m ln(aA) + n ln(aB) > (∆GAmBn + ∆gs)/кТ
При этом характер зависимости размера критического радиуса зародыша от величины поверхностной энергии и энергии упругой деформации качественно остается неизменным.
Как уже указывалось ранее, повышение уровня когерентности межфазной границы в большинстве случаев не только понижает поверхностную энергию (положительный эффект), но и повышает энергию упругой деформации (отрицательный эффект).
Однако, в принципе, можно разработать стали и сплавы такого химического состава, что образующиеся в твердом растворе когерентные мелкодисперсные частицы химических соединений практически только снижают поверхностную энергию. Например, в структуре жаропрочных аустенитных никелевых сплавов присутствуют когерентные мелкодисперсные частицы гамма штрих - фазы, с периодом кристаллической решетки всего на 0,1% отличающейся периода решетки аустенита.
Рассмотренные теории относятся к случаю «гомогенного» зарождения. Однако может быть сделано формальное расширение данной теории и для описания «гетерогенного» зарождения, когда зародыши образуются на межзеренных границах, дефектах упаковки или дислокациях, путем учета следующего обстоятельства: энергия образования зародыша понижается за счет поверхностной энергии этих дефектов.