Тема 9. Обратная задача динамики

I: 173.

S: Сила F сообщает ускорение телу массой m₁ ускорение а₁ = 2,0 м/с², телу массой m₂ ускорение а₂ = 3,0 м/с². Какое ускорение а₃ под действием той же силы получат оба тела, если их соединить вместе? а₃ = …(м/с²).

+: 1,2

I: 174.

S: Одинаковые грузы массой 120 г каждый прикреплены к нити, переброшенной через блок. На один из грузов действует вертикально вниз сила 48 мН (миллиньютон) (см. рис.). Какой путь пройдёт каждый из грузов за 2 с?

s = …(см)

+: 40

I: 175.

S: Материальная точка массы m = 2 кг движется по криволинейной траектории под действием силы F = 3ּτ + 4ּn (H). Определить ускорение точки (м/с²).

Отметьте правильный ответ.

-: 2ּ; +: 2,5; -: 5,0; -: 7,2

I: 176.

S: Тело массой m = 20 кг падает по вертикали, сила сопротивления воздуха R = 0,04ּv² (Н). (Ускорение свободного падения в вакууме принять равным g = 9,8 м/с².) Определить максимальную скорость падения тела (м/с).

Отметьте правильный ответ.

-: 9,8; -: 50; +: 70; -: 100

I: 177.

S: Моторная лодка массой m = 200 кг после остановки мотора движется прямолинейно, преодолевая сопротивление воды. Сила сопротивления R = 4ּv² (Н). Определить ускорение (м/с²) лодки (как алгебраическую величину), когда её скорость v = 5 м/с.

Отметьте правильный ответ.

-: 0; -: – 0,2; +: – 0,5; -: – 1,0

I: 178.

S: Тело массой m = 1 кг падает по вертикали, сила сопротивления воздуха R = 0,03ּv (Н). Определить максимальную скорость падения тела (ускорение свободного падения в вакууме принять равным g = 9,8 м/с²; результат вычисления округлить до ближайшего целого числа.); v = … (м/с)

+: 327

I: 179.

S: Груз массы m = 100 кг, лежащий на полу кабины опускающегося лифта, давит на пол с силой F_давл. = 1030 Н. Найти модуль ускорения а лифта (ускорение свободного падения принять равным g = 9,8 м/с²; результат вычисления определить с точностью до первого знака после запятой включительно); а = … ( м/с²).

+: 0,5

I: 180.

S: Два шарика начали одновременно и с одинаковой скоростью двигаться по поверхностям, имеющим форму, изображённую на рис. Как будут отличаться времена движения шариков к моменту их прибытия в точку В ? Трением пренебречь.

Отметьте правильный ответ

-: Оба шарика достигнут точки В одновременно

-: Шарик 1 достигнет точки В раньше шарика 2

+: Шарик 2 достигнет точки В раньше шарика 1.

I: 181.

S: Груз массой m может скользить без трения по стержню, укреплённому перпендикулярно к оси ОА (см. рис.) центробежной машины. Груз соединяют с осью пружиной с коэффициентом жёсткости с. При какой угловой скорости ω пружина растянется на 60% первоначальной длины?

ω = …

(вместо многоточия подставить соответствующий множитель в виде десятичной дроби; результат вычисления округлить до второго знака после запятой включительно).

+: 0,61

I: 182.

S: С какой наибольшей скоростью может двигаться автомобиль на повороте радиусом закругления R = 150 м, чтобы не «занесло», если коэффициент трения скольжения шин о дорогу k = 0,42? (Ускорение свободного падения в вакууме принять равным g = 9,8 м/с²; результат вычисления округлить до ближайшего целого числа.) v = … (м/с).

+: 25

I: 183.

S: Люстра массой m = 100 кг подвешена к потолку на металлической цепи, длина которой l = 5 м. Определить высоту h(м), на которую можно отклонить люстру, чтобы при последующих качаниях цепь не оборвалась? Известно, что разрыв цепи наступает при натяжении Т = 1960 Н (Ускорение свободного падения принять равным g = 9,8 м/с².)

h < … (м).

+: 2,5

I: 184.

S: Найти период вращения маятника, совершающего круговые движения в горизонтальной плоскости. Длина нити l = 1 м. Угол, образуемый нитью с вертикалью, α = 30^о (см. рис.). (Ускорение свободного падения в вакууме принять равным g = 9,8 м/с²; результат вычисления округлить с точность до второго знака после запятой включительно.)

Т = … (сек)

+: 1,87

I: 185.

S: На повороте дороги радиусом R = 100 м равномерно движется автомобиль. Центр тяжести находится на высоте h = 1 м, ширина следа автомобиля а = 1,5 м. Определить скорость v_кр, при которой автомобиль может опрокинуться. В поперечном направлении автомобиль не скользит. (Ускорение свободного падения в вакууме принять равным g = 9,8 м/с²; результат вычисления округлить до ближайшего целого числа.) v_кр = … (м/с).

+: 27

I: 186.

S: Грузик подвешен на нерастяжимой нити длиной l. Какую минимальную скорость нужно сообщить грузику в нижнем положении 1, чтобы он мог вращаться в вертикальной плоскости (смог пройти верхнюю точку 2) (см. рис.).

v_min = …(вместо многоточия подставить соответствующий множитель в виде десятичной дроби; результат вычисления округлить до второго знака после запятой включительно).

+: 2,24

I: 187.

S: Человек сидит на краю круглой горизонтальной платформы радиусом R = 4 м. Сколько оборотов n в минуту должна делать платформа вокруг вертикальной оси, чтобы человек не смог удержаться на ней при коэффициенте трения f = 0,29? (Ускорение свободного падения в вакууме принять равным g = 9,8 м/с²; результат вычисления округлить до целого числа.) n = … (об/мин).

+: 8

I: 188.

S: Грузик подвешен на жёстком невесомом стержне длиной l. Какую минимальную скорость нужно сообщить грузику в нижнем положении 1, чтобы он мог вращаться в вертикальной плоскости (смог пройти верхнюю точку 2) (см. рис.).

v_min = …(вместо многоточия подставить соответствующий множитель).

+: 2

I: 189.

S: Внутри конической поверхности обращается шарик по окружности радиусом R = 50 см (см. рис.). Определить период обращения шарика по окружности. Угол при вершине конуса 2α (α = 30^о). (Ускорение свободного падения в вакууме принять равным g = 9,8 м/с²; результат вычисления округлить до целого числа.)

Т = … (сек).

+: 1

I: 190.

S: На горизонтальной доске лежит брусок. Какое ускорение a в горизонтальном направлении следует сообщить доске, чтобы брусок соскользнул с неё? Коэффициент трения между бруском и доской k = 0,2. (g = 9,81 м/с²). (Результат вычисления округлить до второго знака после запятой включительно.) a > …(м/с²).

+: 1,96

I: 191.

S: Космонавты, высадившиеся на поверхности Марса, измерили период обращения конического маятника, представляющего собой небольшое тело, прикреплённое к нити и движущееся по окружности в горизонтальной плоскости с постоянной скоростью (см. рис.). Период оказался равным Т = 3 сек. Длина нити l = 1 м. Угол создаваемый нитью с вертикалью, α = 30^о. Найдите по этим данным ускорение свободного падения на Марсе.

Результат вычисления округлить до первого знака после запятой включительно. g = … (м/с²).

+: 3,8

I: 192.

S: Какую начальную скорость v_о имел снаряд, вылетевший из пушки под углом α = 30^о к горизонту, если он пролетел расстояние s = 17 300 м? Известно, что сопротивление воздуха уменьшило дальность полёта в 4 раза.

(Ускорение свободного падения в вакууме принять равным g = 9,8 м/с²; результат вычисления округлить до целого числа.) v_о = … (м/с)

+: 885

I: 193.

S: Матер. точка массы m = 1 кг движется вдоль горизонтальной оси Ox под действием силы (H). Полагая начальные условия движения точки нулевыми, найти координату x точки в момент времени t = 1 с. (Результат вычисления округлить до первого знака после запятой включительно.) x = … (м).

+: 0,7

I: 194.

S: Матер. точка массы m = 2 кг движется вдоль горизонтальной оси Ox под действием силы (H), график изменения проекции F_x которой с течением времени представлен на рисунке. Принимая, что при t₀ = 0 x = x₀ = 0 и , определить скорость точки после прекращения действия силы, если F₁ = 24 (Н), а F₂ = 9 (Н).

v = … (м/с).

+: 3

I: 195.

S: Матер. точка массы m движется вдоль горизонтальной оси Ox под действием силы (H), график изменения проекции F_x которой с течением времени представлен на рисунке. Принимая, что при t₀ = 0 x = x₀ = 0 и , определить скорость точки после прекращения действия силы.

v = … (вместо многоточия подставить соответствующий множитель).

+: v = 0.

I: 196.

S: Искусственный спутник Земли, обращающийся по круговой орбите, переводится на другую круговую орбиту, радиус которой в 4 раза больше радиуса исходной орбиты.

Во сколько раз изменяется скорость движения спутника по орбите? v₂/v₁ = …

+: 0,5

I: 197.

S: Матер. точка массы m = 1 кг движется вдоль горизонтальной оси Ox под действием силы сопротивления, пропорциональной скорости v (F_сопр = kּv, k = 0,1 Нּсек/м). Какое расстояние s пройдёт матер. точка, прежде чем её скорость уменьшится в 2 раза? Начальная скорость точки равна v₀ = 2 м/с. s = … (м).

+: 10

I: 198.

S: Матер. точка массы m = 1 кг движется вдоль горизонтальной оси Ox под действием силы ; график изменения проекции силы на эту ось с течением времени представлен на рисунке.

Определить скорость точки в момент времени t = 10 с, если F₀ = 10 (Н), а начальные условия движения точки - нулевые. v = … (м/с).

+: 40

I: 199.

S: Матер. точка массы m = 1 кг движется вдоль горизонтальной оси Ox под действием силы F_х = (1 + x) (Н). Начальная скорость v₀ = 1 м/с. Определить закон движения матер. точки.

Отметьте правильный ответ.

-: x = sin(t) - cos (t) + 1

-: x = sin (t) + cos(t) – 1

-: x = 0,5ּe ^t + 0,5ּe^{- t} – 1

+: x = e ^t - 1

I: 200.

S: Матер. точка массы m = 1 кг движется вдоль горизонтальной оси Ox под действием силы сопротивления, пропорциональной скорости v (F_сопр = kּv, k = 0,1 Нּсек/м). За какое время t₁от начала движения скорость точки уменьшится в 2 раза? Начальная скорость точки равна v₀ = 2 м/с. (Результат вычисления округлить до целого числа.) t = … (сек).

+: 7

I: 201.

S: Матер. точка массы m = 1 кг совершает прямолинейное движение под действием силы F = 3ּsin(t) (Н). (Аргумент функции sin(t) – в радианах!) Начальная скорость матер. точки равна нулю. Определить расстояние, на которое переместится точка за время 1,5 сек. (Результат вычисления округлить до первого знака после запятой включительно.) s = … (м).

+: 1,5

I: 202.

S: Матер. точка массы m = 1 кг совершает прямолинейное движение под действием силы F = 4ּcos(t) (Н). (Аргумент функции cos(t) – в радианах!) Начальная скорость матер. точки равна нулю. Определить расстояние, на которое переместится точка за время 1,5 сек. (Результат вычисления округлить до первого знака после запятой включительно.) s = … (м).

+: 3,7

I: 203.

S: Матер. точка массы m = 1 кг движется вдоль горизонтальной оси Ox под действием силы F_х = 3ּ(Н). Начальная скорость точки равна v₀ = 1 м/с. Определить расстояние, на которое переместится точка за время 1 сек. (Результат вычисления округлить до первого знака после запятой включительно.)

s = … (м).

+: 4,7

I: 204.

S: Матер. точка массы m = 1 кг движется вдоль горизонтальной оси Ox под действием силы F_х = - 4ּ(Н). Начальная скорость точки равна v₀ = 1 м/с. Начальное положение точки принять за начало отсчёта. Определить закон движения точки.

Отметьте правильный ответ.

-: x = e^{– 2ּt} + tּe ^{– 2ּt} – 1

-: x = e^–2ּt – 1

+: x = tּe^{– 2ּt}

-: x = e^{– 2ּt} + tּe^{– 2ּt} + t² + 2ּt – 1

-: x = e^{– t} – e^{– 2ּt}

I: 205.

S: Матер. точка массы m = 1 кг движется вдоль горизонтальной оси Ox под действием силы F_х = - (Н). Начальная скорость точки равна нулю; начальное смещение х₀ = 1 м. Определить закон движения точки.

Отметьте правильный ответ.

-: x = 0,5ּ(3ּe^–0,5ּt – e^–1,5ּt)

+: x = e ^{– 0,5ּt}[cos ]

-: x = 2ּ(e^{– t} – 0,5ּe^–2ּt )

-: x = e ^{– t} + tּe ^{– t} .

I: 206.

S: Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от центра О и направленной к этому центру , где - радиус-вектор точки, c - коэффициент пропорциональности. В начальный момент матер. точка находилась в точке М₀ с координатами х = х₀ и у = 0 и ей сообщили начальную скорость ₀, направленную параллельно оси Oy т.е. v_0x = 0, v_0y = v₀. Найти уравнение траектории матер. точки.

Отметьте правильный ответ.

-: x² + y² = x₀²

-: x² + y² = ּv₀²

+: + ּ = 1

-: – ּ = 1.

I: 207.

S: Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы отталкивания от неподвижного центра О, изменяющейся по закону пропорциональной смещению точки от центра О и направленной к этому центру = k²ּmּ, где - радиус-вектор точки. В начальный момент точка находилась в М₀ с координатами х = х₀ и у = 0 и ей сообщили начальную скорость ₀, направленную параллельно оси Oy т.е. v_0x = 0, v_0y = v₀. Найти уравнение траектории точки.

Отметьте правильный ответ.

-: x² + y² = x₀²

-: x² – y² =

+: – ּ = 1

-: + ּ = 1.

I: 208.

S: Матер. точка массы m движется с начальной скоростью v₀ = 1 м/с в среде с сопротивлением. Сила сопротивления пропорциональна кубичному корню скорости матер. точки и по величине равна kּ, k = 0,3ּm – коэффициент сопротивления. Определить расстояние s, которое пройдёт матер. точка до остановки; s = … (м).

+: 2

I: 209.

S: Матер. точка массы m движется с начальной скоростью v₀ = 1 м/с в среде с сопротивлением. Сила сопротивления пропорциональна кубичному корню скорости матер. точки и по величине равна kּ, k = 0,3ּm – коэффициент сопротивления. Определить время t₁, за которое пройдёт матер. точка до остановки; t₁ = … (сек.).

+: 5

I: 210.

S: Два геометрически равных и однородных шара сделаны из различных материалов – 1) из железа и 2) фарфора. Плотности материалов соответственно: железа ρ₁ = 7,9ּ10³ кг/м³, фарфора ρ₂ = 2,3ּ10³ кг/м³. Оба шара падают в воздухе. Сопротивление среды пропорционально квадрату скорости (R = kּv²). Определить отношение максимальных скоростей шаров. (Результат вычисления округлить до второго знака после запятой включительно.) v_1max / v_2max = …

+: 1,85

I: 211.

S: Матер. точка массы m = 2 кг движется в горизонтальной оси Ox под действием силы , график изменения проекции F_x которой с течением времени представлен на рис., где F₀ = 4 (Н). Начальная скорость матер. точки равна 6 м/с. Определить скорость точки в момент времени t ₁ = 10 сек.

v₁ = … (м/с).

+: 0

I: 212.

S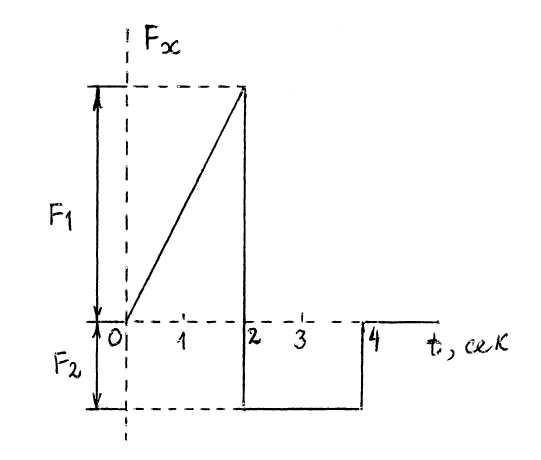: Матер. точка массы m = 2 кг движется в горизонтальной оси Ox под действием силы , график изменения проекции F_x которой с течением времени представлен на рис. Принимая, что при t = 0 x = x₀ = 0 и = 2 м/с, определить скорость точки после прекращения действия силы, если F₁ = 24 (Н), F₂ = 9 (Н).

v = … (м/с).

+: 5

I: 120.