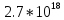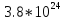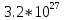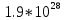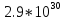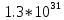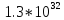- •1 Исследование линейной части системы
- •Построение функциональной схемы системы
- •Построение структурной схемы системы
- •2 Исследование нЕлинейной части системы
- •2.2 Упрощение нелинейной системы
- •2.3 Построение фазового портрета и переходного процесса
- •3 Исследование дискретной части системы
- •3.1 Добавление в систему дискретного элемента
- •3.3 Построение графика переходного процесса, лачх и лфчх
- •3.4 Критерий устойчивости Шур-Кона

СОДЕРЖАНИЕ
Введение 3
-
Исследование линейной части системы 4
1.1 Построение функциональной схемы системы 4
1.2 Построение структурной схемы системы 4
1.3 Определение устойчивости системы по критерию Гурвица и
Михайлова 6
1.4 Построение переходного процесса и амплитудно-частотной
характеристики системы 11
1.5 Построение логарифмической амплитудно – частотной и
фазочастотной характеристик системы. Нахождение запасов
устойчивости
14
2 Исследование нелинейной части системы 17
2.1 Добавление нелинейного элемента в структурную схему 17
системы
2.2 Упрощение нелинейной системы 18
2.3 Построение фазового портрета и переходного процесса 18
3 Исследование дискретной части системы 22
3.1 Добавление в систему дискретного элемента 22
3.2 Z-преобразование непрерывной части 22
3.3 Построение графика переходного процесса, ЛАЧХ и ЛФЧХ 23
3.4 Критерий устойчивости Шур-Кона 25
Список использованных источников 26
ВВЕДЕНИЕ
Основная задача автоматизации состоит в том, чтобы обеспечивать полное или частичное исключение человека из процесса производства. Для того чтобы управлять требуемым объектом без непосредственного участия человека, создаются, моделируются и анализируются различные системы, чтобы на основе расчетов улучшить систему существующую или разработать принципиально новую. При этом анализируются устойчивость системы при различных возмущающих воздействиях различными методами, определяются запасы устойчивости, динамические и статические, косвенные и прямые характеристики.
Любые системы автоматического управление (САУ) можно разделить на линейные и не линейные, непрерывные и дискретные, детерминированные и стохастические, статические и астатические, цифровые и импульсные и так далее.
В данной курсовой работе будет исследоваться линейную и нелинейную системы управления приточно-вытяжной вентиляционной установки. Также будет проведено исследование устойчивости системы и определены ее основные характеристики.
1 Исследование линейной части системы
-
Построение функциональной схемы системы
На основе имеющейся функционально–принципиальной схемы построим функциональную схему системы.

Y(t)
З1
ВН
ВО
Вент.
П
Ф
x(t)









Ф
З2


x(t) – регулируемая величина – подача сжатого воздуха; y(t) – выходная величина –показания измерения плотномера.
Рисунок 1 – Функциональная схема САР для вентиляции помещения
Функциональная схема – это схема, состоящая из функциональных элементов, которые показывают их функциональное назначение при автоматическом управлении технологическим процессом и связь между ними.
-
Построение структурной схемы системы
На основе полученной функциональной схемы построим структурную схему системы.
Структурная схема системы автоматического управления отражает прохождение и преобразование сигналов в звеньях системы управления(Рисунок 2).
В структурную схему входят 8 элементов.
W2

W3

W1
W4
W5






W6


W7
W8


W1 – передаточная функция заслонки 1; W2 – передаточная функция фильтра 2; W3 – передаточная функция воздухонагревателя 3; W4 – передаточная функция воздухоохладителя 4; W5 – передаточная функция вентилятора 5; W6 – передаточная функция помещение 6; W7 – передаточная функция фильтр 7; W8 – передаточная функция заслонки 8.
Рисунок 2 – Структурная схема САР для приточно-вытяжной вентиляционной установки
Передаточная функция заслонки 1 имеет вид колебательного звена:
 ,
,
где К1 = 1,2 – коэффициент передачи;
Т1 =0,12– постоянная времени;
Т2 =0,12– постоянная времени;
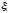 =0,06
– коэффициент демпфирования.
=0,06
– коэффициент демпфирования.
Передаточная функция фильтра 2 имеет вид усилительного звена:
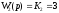 ,
,
где К2 = 3 – коэффициент передачи;
Передаточная функция воздухонагревателя 3 имеет инерционного звена первого порядка:
 ,
,
где К3 = 3,5 – коэффициент передачи;
Т3 =35– постоянная времени.
Передаточная функция воздухоохладитель 4 имеет вид инерционного звена первого порядка:
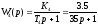 ,
,
где К4 = 3,5 – коэффициент передачи;
Т4 =35– постоянная времени.
Передаточная функция вентилятора 5 имеет вид инерционного звена первого порядка:
 ,
,
где К5 = 4 – коэффициент передачи;
Т5 = 1,4 – постоянная времени.
Передаточная функция помещения 6 имеет вид инерционного звена первого порядка:
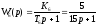 ,
,
где К6 = 5 – коэффициент передачи;
Т6 = 15 – постоянная времени
Передаточная функция фильтра 7 имеет вид усилительного звена:
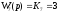 ,
,
где К7 = 3 – коэффициент передачи;
Передаточная функция заслонки 8 имеет вид колебательного звена:
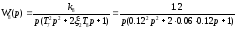 ,
,
где К8 = 1,2 – коэффициент передачи;
Т7 =0,12– постоянная времени;
Т8 =0,12– постоянная времени;
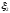 =0,06
– коэффициент демпфирования.
=0,06
– коэффициент демпфирования.
-
Определение устойчивости системы по критерию Гурвица и Михайлова
Применяя правила преобразования структурных схем, упростим нашу схему.
Преобразуем структурную схему:
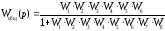
Подставив
значения передаточных функций в формулу
для
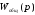 ,
получим следующий вид уравнения:
,
получим следующий вид уравнения:


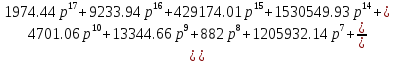
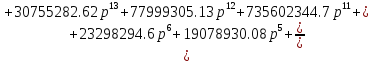


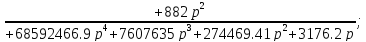
Получили выражение общей передаточной функции:
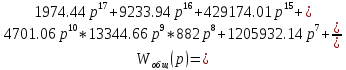





Определяем устойчивость по критерию Гурвица.
Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительными.
Характеристическое уравнение имеет вид:
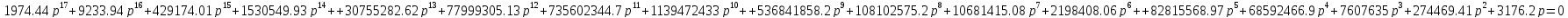
В характеристическом уравнении не все коэффициенты, значит необходимое условие устойчивости не выполняется.
По коэффициентам характеристического уравнения составляется определитель Гурвица.
Для этого по главной диагонали определителя выписываются все коэффициенты характеристического уравнения, начиная со второго, затем вверх записываются коэффициенты с возрастающим индексом, а вниз с убывающим индексом.
Составленный определитель называется главным определителем Гурвица, он имеет порядок, совпадающий с порядком характеристического уравнения. Из главного определителя составляются частные определители первого, второго, третьего и так далее порядков их образования из главного определителя.
Вычисляя главный определитель и частные определители, Гурвиц установил: для того, чтобы система была устойчива необходимо и достаточно, чтобы все определители были положительны.
Если хотя бы один определитель отрицательный, то система неустойчива.
Порядок
характеристического уравнения:
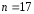 .
.
Коэффициенты характеристического уравнения:
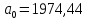

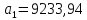
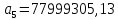


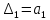
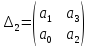
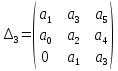
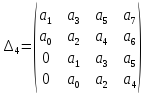
Подставим значения коэффициентов характеристического уравнения, получим следующее коэффициенты:
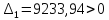 ;
;

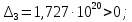
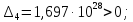
Вывод: определителя Гурвица положителен, значит вещественная часть корней характеристического уравнения отрицательна, и, согласно теореме Ляпунова, система устойчива.
Определяем устойчивость по критерию Михайлова.
Характеристическое уравнение имеет вид:
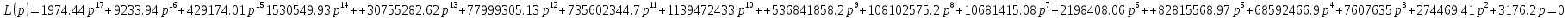
Путем
замены
 ,
получим характеристический вектор.
,
получим характеристический вектор.
Выделим вещественную и мнимую части:
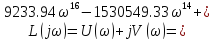
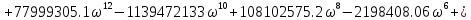
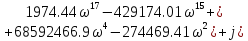

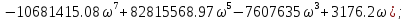
Для построения годографа Михайлова
Таблица 1 - Годограф Михайлова
|
n |
u(w) |
v(w) |
|
0 |
0 |
0 |
|
10 |
|
|
|
20 |
|
|
|
30 |
|
|
|
40 |
|
|
|
50 |
|
|
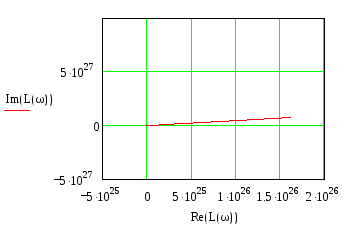



Рисунок 3 – Годограф Михайлова
Вывод: годограф Михайлова системы 17-ого порядка при изменении частоты от 0 до 50 не проходит последовательно против часовой стрелки по всем квадрантам, начиная с вещественной оси и во I-ом квадранте уходит в бесконечность.
Из этого следует, что данная система автоматического управления находится в не устойчивом состоянии.
1.4 Построение переходного процесса и амплитудно – частотной харак-
теристики системы
Переходная функция - это реакция системы на ступенчатое входное воздействие.
Передаточная функция системы имеет вид:
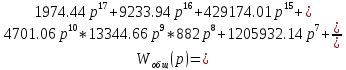
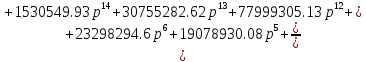
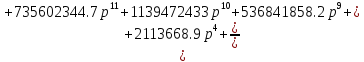
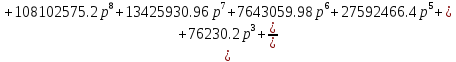

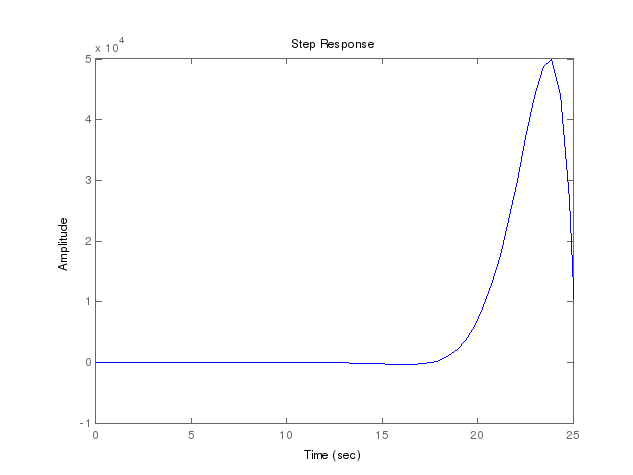
Для построения переходного процесса используем программу MATLAB. Построим переходный процесс системы командой step(w)(Рисунок 4).
Прямые оценки качества системы определить по графику не возможно так как система не устойчива.
Построим амплитудно – частотную характеристику системы.
Амплитудно–частотная характеристика строится для того, чтобы определить косвенные оценки качества системы.
25
0
5
10
15
20
0
-1
4
3
2
1
5
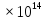
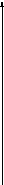
t, с
h(t)



Рисунок 4 - График переходного процесса
Для того, чтобы определить амплитудно – частотную характеристику системы, необходимо в передаточной функции W(p) р заменить на jω, выделить мнимую и вещественную части, по формуле определить амплитудно – частотную характеристику системы:

где
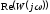 – действительная часть передаточной
функции;
– действительная часть передаточной
функции;
 – мнимая
часть передаточной функции.
– мнимая
часть передаточной функции.
Используя прикладную программу MathCAD, вычислим амплитудно – частотную характеристику системы.

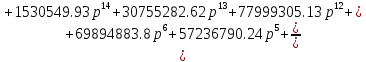

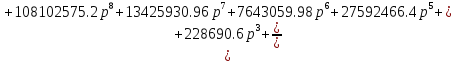

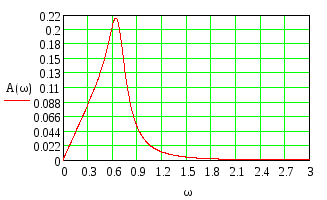
Воспользуемся программой MathCAD для построения графика АЧХ:
![]()
ω,Гц





Рисунок
5 – Амплитудно – частотная характеристика
системы

Определим по графику косвенные оценки качества системы:
– амплитуда при нулевой частоте A(0) =0;
– максимальная амплитуда Аmax =0,22;
– резонансная частота ωp =0,7;
– частота среза: ωср =∞;
– полоса
пропускания:
 0,5
-0,8
0,5
-0,8
– показатель
колебательности:
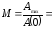 ∞
∞
1.5 Построение логарифмической амплитудно – частотной и фазочастотной характеристик системы. Нахождение запасов устойчивости
Для построения логарифмической амплитудо – частотной характеристи-
ки и логарифмической фазочастотной характеристики разомкнем систему в обратной связи и рассчитаем передаточную функцию разомкнутой системы.


Рисунок 6 – Разомкнутая система
Передаточная функция разомкнутой системы имеет вид:

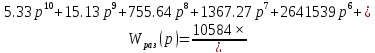
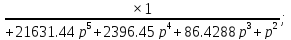
Для построения логарифмической амплитудо – частотной характеристи-
ки и логарифмической фазочастотной характеристики, используем программу MATLAB (рисунок 7).
Определяем
запас устойчивости по амплитуде (рисунок
10). Из точки
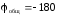 проводим прямую вертикально вверх до
пересечения с ЛАЧХ и находим точку
пересечения:
проводим прямую вертикально вверх до
пересечения с ЛАЧХ и находим точку
пересечения:
 200
дБ
200
дБ
Определяем
запас по фазе. Из точки
 проводим прямую вертикально вниз до
пересечения с ЛФЧХ и находим:
проводим прямую вертикально вниз до
пересечения с ЛФЧХ и находим:
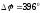
Передаточная функция аппроксимированной логарифмической амплитудно – частотной характеристики запишется в виде:

Определим постоянную времени Т.
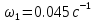


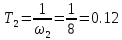
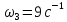
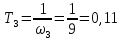
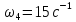
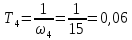

L(ω), дБ
φ(ω), ºС

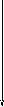
ω, дек




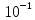


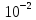
400
200
0
-200
-180
-360
-540
-720
-900
-400
Рисунок 7 – логарифмической амплитудо – частотной характеристи-
ки и логарифмической фазочастотной характеристики системы

L(ω), дБ


ω,дек
φ(ω), ºС



400
200
0
-200
-100
-360
-540
-720
-900
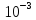

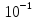
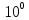
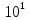


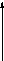


Рисунок 8 – Определение запасов устойчивости системы по фазе и по
амплитуде
Определим коэффициент усиления К.
20lgK = 200
lgK = 10
K
=
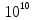 =
=

Тогда передаточная функция аппроксимированной логарифмической амплитудно – частотной характеристики будет иметь следующий вид: