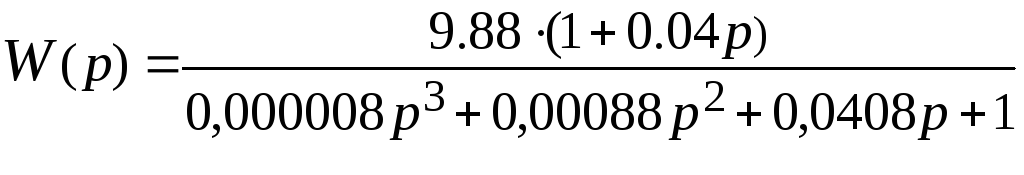Расчет внутреннего контура на мо

Неизменяемая часть:

Такая неизменяемая часть характерна для многих объектов управления, в данном случае для якорной цепи ДПТ.

- тиристорный преобразователь;

- якорная цепь, причем <<;

- датчик тока.

Передаточная функция неизменяемой части как объекта управления:

=

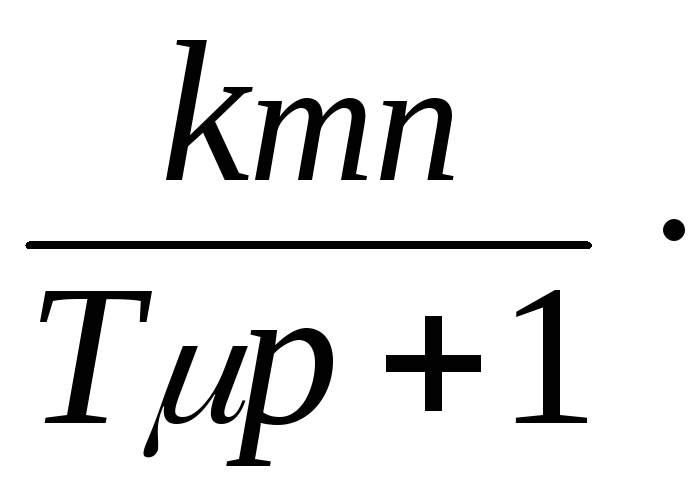
Выбираем ПИ-регулятор, т.к. статическая ошибка должна быть исключена. Передаточная функция ПИ-регулятора будет следующей:

Соответственно передаточная функция разомкнутой САР (разрыв после датчика тока) будет следующей:

Для уменьшения порядка расчета следует принять T_рт=T_я. Это тем более обосновано, что регулятор W_рт(p) должен компенсировать инерционное действие большей постоянной времени Т_я.

В этом случае после сокращения (1+Т_ртр) и (1+Т_яр) получаем:

Задача синтеза теперь состоит в определении коэффициента k_pт, обеспечивающий оптимальный переходной процесс по задающему сигналу U_з, т.е. настройку на МО (модульный оптимум).

Для этого рассмотрим передаточную функцию замкнутой САР:

В результате получили передаточную функцию 2-го порядка, поэтому нужно сравнивать коэффициенты при степенях p с соответствующими коэффициентами при степенях p фильтра Баттерворта 2-го порядка.

Фильтр Баттерворта 2-го порядка по постоянной времени будет следующим:

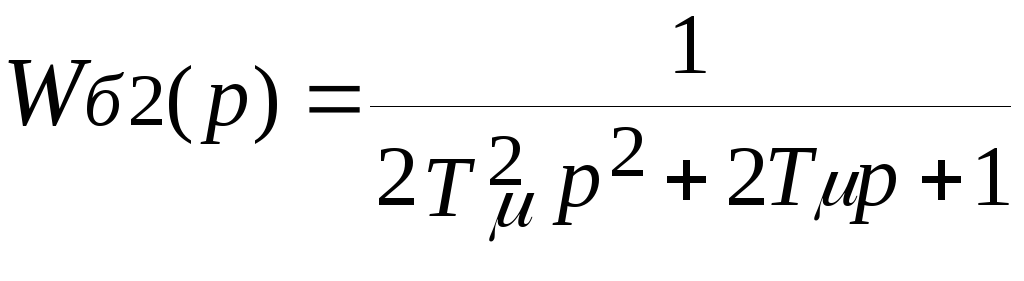
Приравнивая коэффициенты в соответствующих степенях р фильтра Баттерворта и полученной нами передаточной функции замкнутой САР получим следующие равенства:

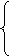
Очевидно, что оба уравнения одинаковы. Из любого уравнения находим k_p:

Определим теперь передаточную функцию оптимизированной САР:

Если система 2-го порядка, коэффициент демпфирования в полученной передаточной функции:

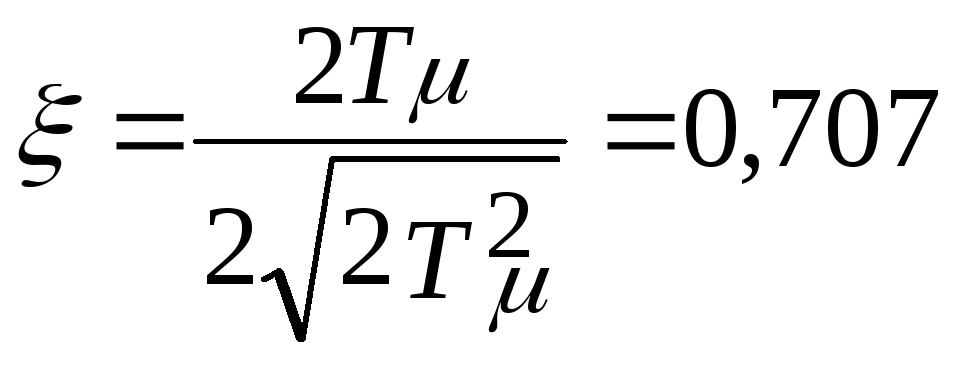
Моделирование внутреннего контура на мо

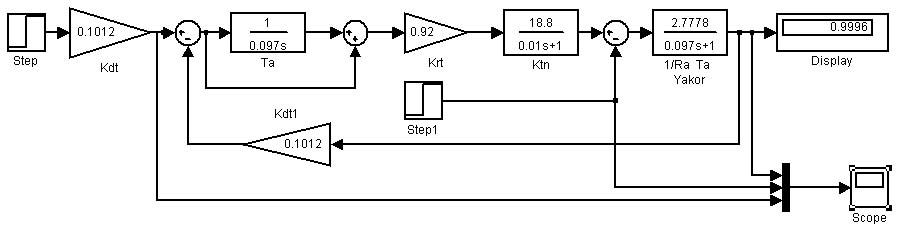
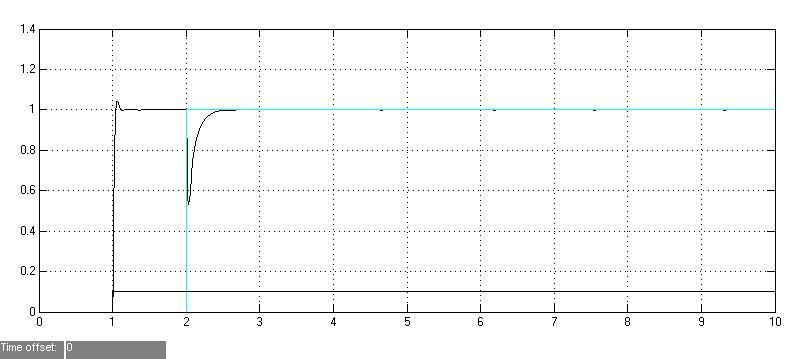
fт

I_я

U _TO

Расчет внутреннего контура на со

Внутренний контур:

-

Определим передаточную функцию внутреннего контура, не принимая условие T_рт=T_я.

Передаточная функция ПИ-регулятора:

Передаточная функция разомкнутого внутреннего контура:

Передаточная функция замкнутого внутреннего контура:

В результате получили передаточную функцию 3-го порядка, т.к. p³ (вместо 2-го порядка при настройке на МО), следовательно, нужно сравнивать коэффициенты при степенях p с соответствующими коэффициентами при степенях p фильтра Баттерворса 3-го порядка, передаточная функция которого имеет вид:

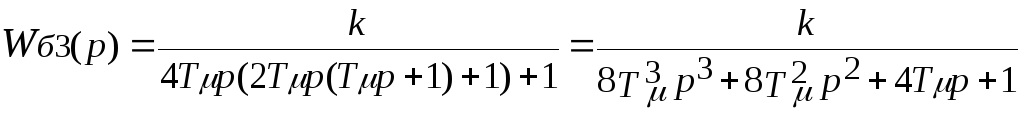
Приравнивая коэффициенты при соответствующих степенях p можно получить следующие три равенства:

;

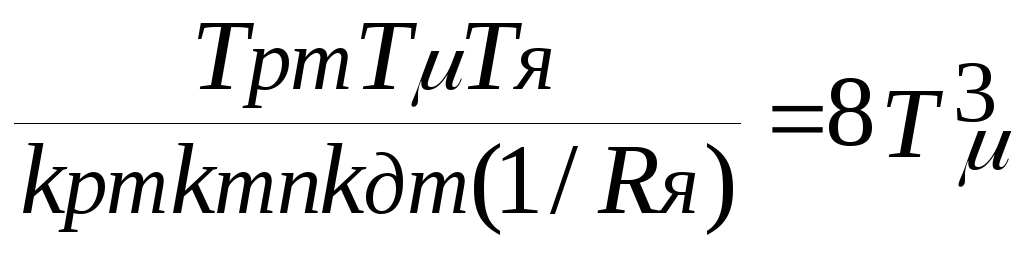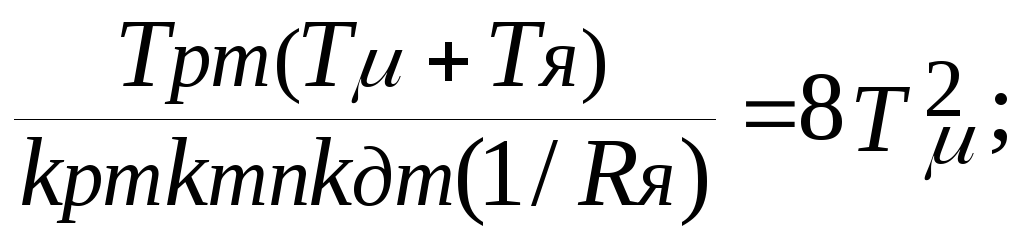
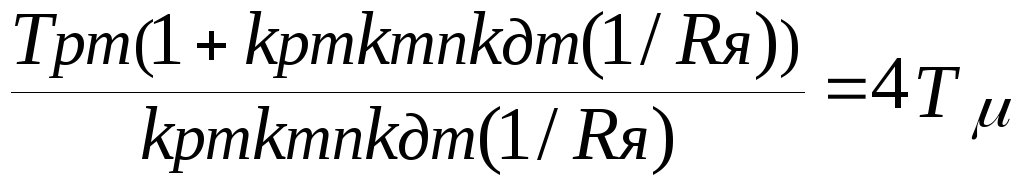
Видно, что в равенствах появляется неоднозначность, связанная с наличием суммы во втором равенстве и сумма обратной величины коэффициентов в третьем равенстве, поэтому возможны следующие варианты расчета:

Вариант А:

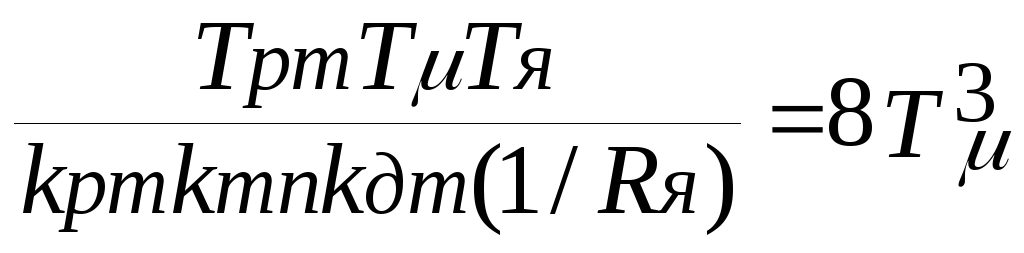
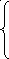
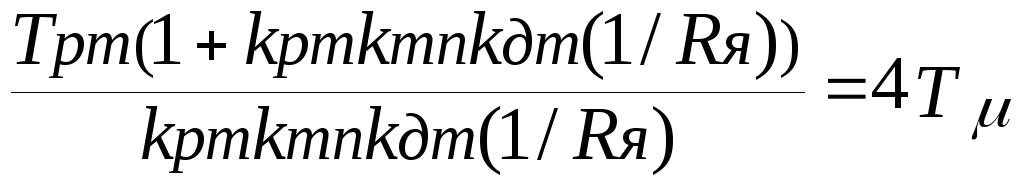
Разделив 1-е равенство на 2-е, получим:

Отсюда найдем k_рт:

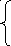
подставив значениеk_рт в 1-е уравнение,

найдемТ_рт

Вариант Б:

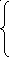
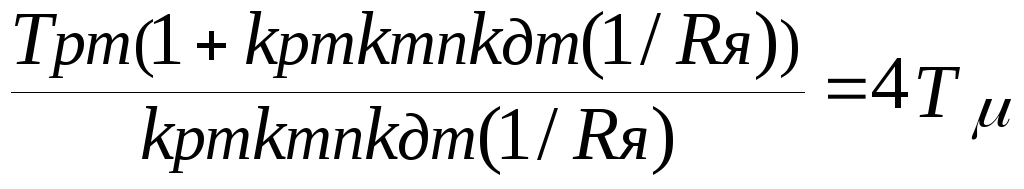
Выполняем ту же последовательность вычислений, что и при варианте А. В результате получим:

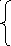
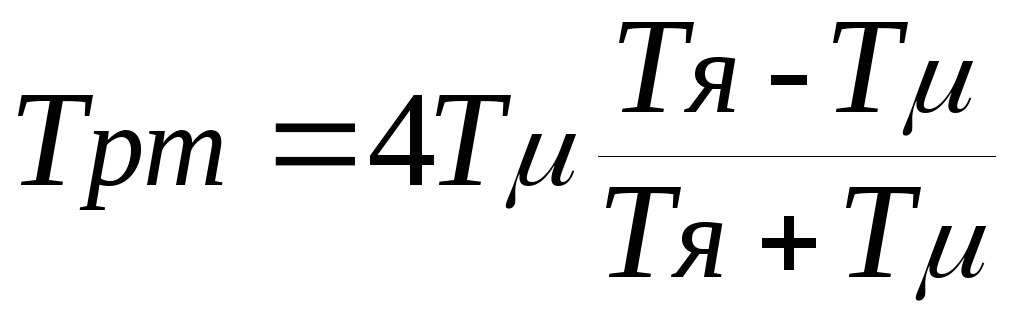
И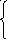з полученных выражений видно, что с погрешностью, обусловленной малой постоянной времени, можно принять:

Соответственно передаточная функция замкнутого внутреннего контура получается близкой к фильтру Баттерворта 3-го порядка с форсирующим звеном (1+4Т_p) в числителе: