Задание

R_я = 0,36 Ом

L_я = 0,040 Гн

U_ян = 188 В

I_ян = 46 А

n_н = 970 об/мин

J = 0,35 кг^.м²

I_ямах = к ^. I_ян = 2,2 ^. 46 = 101.2 А

T_µ =0,01 c

Расчет двигателя постоянного тока как объекта управления

Расчетные схемы двигателя постоянного тока с независимым возбуждением (ДПТ НВ) следующие:

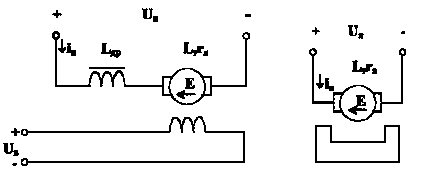
Работа ДПТ НВ описывается следующей системой уравнений:

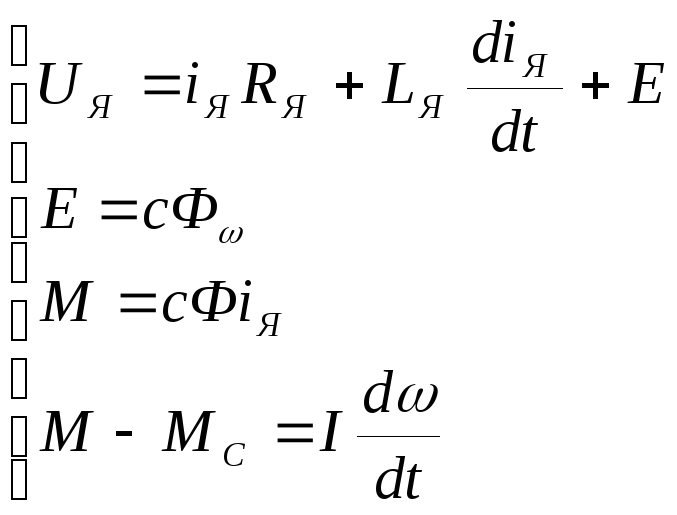(1)

где:

- сопротивление всей якорной цепи;

L_я = L + L_др + L_дп -индуктивность якорной цепи;

Ф - магнитный поток возбуждения;

ω - угловая частота вращения вала ДПТ;

М - вращающий момент, развиваемый ДПТ;

М_с - момент сопротивления от рабочего механизма;

I - момент инерции вращающихся частей (якоря ДПТ и рабочего механизма);

Е- противо ЭДС якоря;

С- электромашинный коэффициент ДПТ.

При расчетах электромеханических параметров ДПТ значение с и Ф отдельно не используются и в паспортных данных их не приводят. Произведение сФ определяется по паспортным данным двигателя для номинального режима в установившемся режиме.

при условии ;

обозначим сФ = к

(В с)

Из двух первых уравнений системы (1) получаем:

(2)

Уравнение (2) - дифференциальное уравнение 1-го порядка для якорной цепи:

входной сигнал- напряжение U_я, выходной сигнал- ток якоря i_Я .В операторной форме записи получим следующее:

(3)

Величина имеет размерность времени [c] и называется электромеханической постоянной времени якорной цепи.

(с)

Используя приращение которое называет приращениеприE=const получаем из (3):

-дифференциальное уравнение в операторной форме.

Получаем передаточную функцию якорной цепи:

- представляет собой аппереодическое звено 1-го порядка.

Теперь исходную систему (1) можно свести в следующую систему:

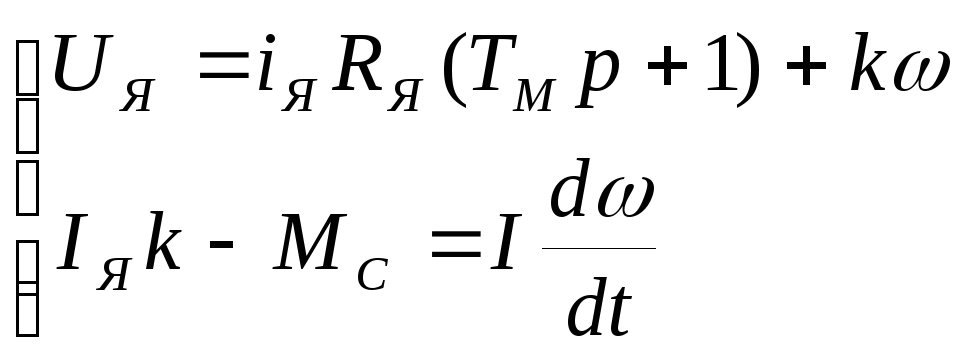(5)

В этой системе уравнений (5) входом ДПТ является напряжение U_я , выходом -частота вращения, нагрузка- М_с, а ток i_я является промежуточной величиной. Решим систему уравнений (5) относительно в зависимости от величин U_я и М_с. Из 2-го уравнения системы (5) находим:

;

Подставим значение в 1-е уравнение системы (5) получим:

;

;

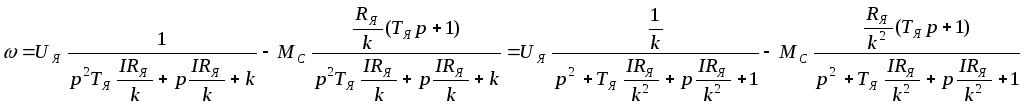Первое слагаемое определяет влияние на напряжение якоря, а второе - влияние момента нагрузкиM_c. Величина имеет размерность времени [c] и называется электромеханической постоянной времени.

(С)

Величина к_д = 1/к – коэффициент передачи двигателя. Вычисляем:

Окончательно получим выражение для передаточной функции ДПТ:

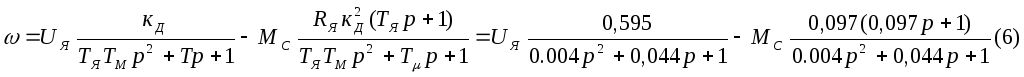
Следует отметить, что в статическом режиме (при р=0) формула (6) совпадает с известной формулой механической характеристики ДПТ:

(7)



U₁<U_ян; U₂<U₁

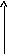
1 2

U_ян 1

2

U₁

U₂t

M

Анализ передаточной функции ДПТ по выражению (6) показывает , что его структурная схема может быть представлена последовательным соединением апериодического звена 1-го порядка и интегрирующего звена, охваченные отрицательной обратной связью.

Условным здесь является сравнение тока якоря с током нагрузки. Получимпередаточную функцию по данной схеме:

что полностью совпадает с передаточной функцией по формуле (6). Поэтому приведенная структурная схема является адекватной и полностью соответствует дифференциальному уравнению ДПТ.

Передаточная функция ДПТ является звеном 2-го порядка. Определим степень колебательности:

Т.к. 0 < < 1 ,то данное звено 2-го порядка является колебательным.