
- •Введение
- •1 Анализ линейной системы автоматического регулирования
- •1.1 Преобразование структурной схемы и определение передаточных функций системы
- •1.2 Исследование системы на устойчивость по критерию Гурвица
- •1.2 Исследование системы на устойчивость по критерию Михайлова
- •1.3 Исследование системы на устойчивость по критерию Найквиста
- •1.4 Определение устойчивости системы по логарифмическим частотным характеристикам
- •2 Синтез линейной системы автоматического регулирования по логарифмическим частотным характеристикам
- •2.1 Построение лачх исходной системы
- •2.2 Построение желаемой лачх
- •2.3 Проверка запаса устойчивости по фазе скорректированной системы
- •2.4 Передаточная функция разомкнутой скорректированной системы
- •2.5 Построение лачх последовательного корректирующего устройства
- •2.6 Передаточная функция корректирующего устройства
- •3 Расчет переходного процесса скорректированной системы
- •3.1 Определение передаточной функции замкнутой скорректированной системы
- •3.2 Расчет вещественной характеристики замкнутой системы
- •3.3 Расчет переходного процесса методом трапеций
- •3.4 Оценка качества переходного процесса
- •4 Выбор схемы и расчет параметров корректирующего устройства
- •4.1 Выбор схемы корректирующего устройства
- •4.2 Принципиальная схема корректирующего устройства
- •4.3 Расчет параметров корректирующего устройства
- •Заключение
- •Библиографический список
1.4 Определение устойчивости системы по логарифмическим частотным характеристикам
А(w) – амплитудная частотная функция, модуль частотной передаточной функции разомкнутой системыW(jw).
φ(w) – аргументW(jw),φ(w)=argW(jw), фазовая частотная функция.
 (18)
(11)
(18)
(11)
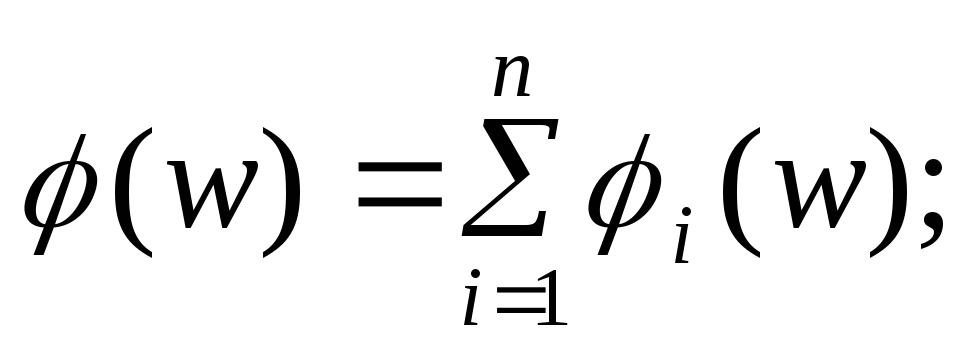 (19)
(12)
(19)
(12)![]() (20)
(13)
(20)
(13)
Найдём ЛАЧХ разомкнутой системы. Для этого проанализируем разомкнутую систему (3):
Звенья
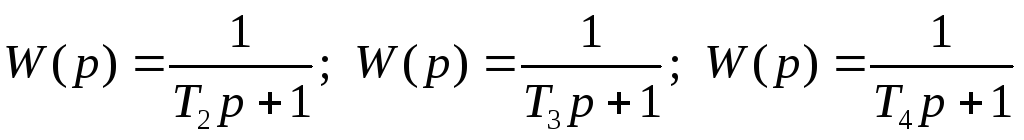 -
инерционные, каждое из этих звеньев
даёт наклон -20 Дб/дек;
-
инерционные, каждое из этих звеньев
даёт наклон -20 Дб/дек;Звено
 - усилительное. Оно даёт нам сдвиг по
осиL(w) на
число 20LogK.
- усилительное. Оно даёт нам сдвиг по
осиL(w) на
число 20LogK.Звено
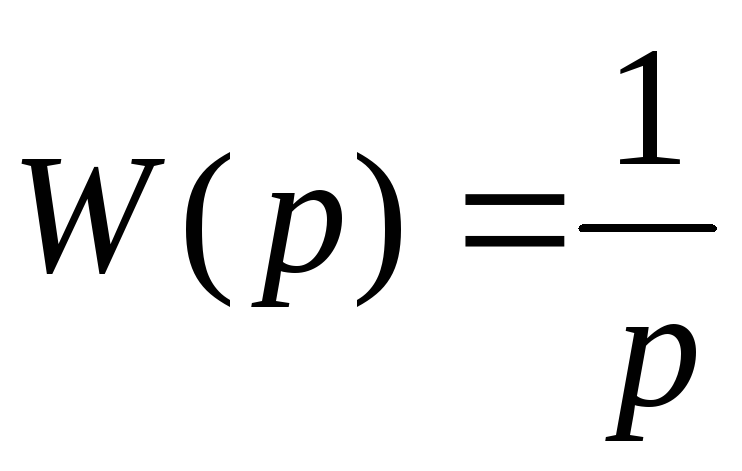 - интегрирующее. Оно даёт нам наклон
-20 Дб/дек.
- интегрирующее. Оно даёт нам наклон
-20 Дб/дек.
Исходя из свойства L(w) можем записать:
![]() (21)
(21)
Найдём сопрягающие
частоты по формуле
![]() (22)
(22)
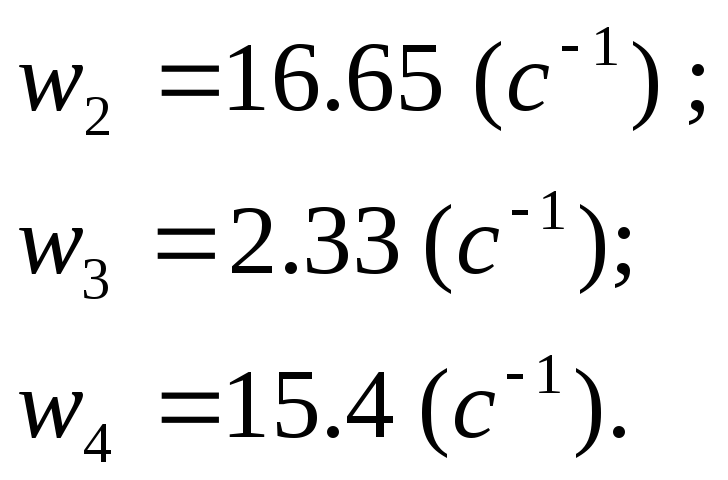
Рассчитаем параметры для построения ЛФЧХ разомкнутой системы, путем суммирования ЛФЧХ всех звеньев.
Значения углов
![]() вычисляются в диапазоне частот от
минимальной частоты, соответствующей
началу координат до частоты, при которой
фазовый сдвиг превышает (–180º).
вычисляются в диапазоне частот от
минимальной частоты, соответствующей
началу координат до частоты, при которой
фазовый сдвиг превышает (–180º).
По свойствам звеньев определим ЛФЧХ для каждого звена по отдельности:
- для усилительного
звена
![]() ;
;
- для инерционного
звена
![]()
-для интегрирующего
![]() .
.
Запишем ЛФЧХ для каждого звена в отдельности
![]() ;
;
![]() ;
;
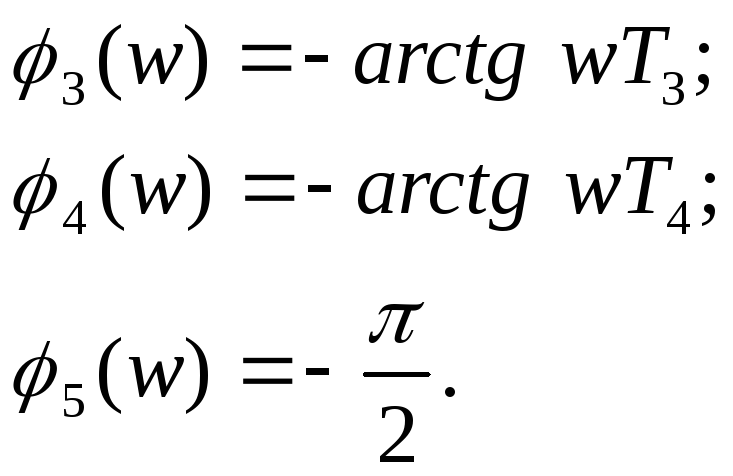
Значения результирующей ЛФЧХ найдем как
![]() (23)
(23)
Таблица 2 – Значения ЛФЧХ
|
Частота |
Звено 1 усилительное |
Звено 2 инерционное |
Звено 3 инерционное |
Звено 4 инерционное |
Звено 5 интегратор |
Результирующая ЛФЧХ | |||
|
|
w*T2 |
|
w*T3 |
|
w |
φ4(ω) |
φ5(ω) |
| |
|
0,1 |
0 |
0,006 |
-0,344 |
0,043 |
-2,462 |
0,007 |
-0,372 |
-90,000 |
-93,179 |
|
0,3 |
0 |
0,018 |
-1,031 |
0,129 |
-7,351 |
0,020 |
-1,117 |
-90,000 |
-99,500 |
|
0,5 |
0 |
0,030 |
-1,718 |
0,215 |
-12,135 |
0,033 |
-1,862 |
-90,000 |
-105,715 |
|
0,7 |
0 |
0,042 |
-2,405 |
0,301 |
-16,753 |
0,046 |
-2,605 |
-90,000 |
-111,764 |
|
0,9 |
0 |
0,054 |
-3,091 |
0,387 |
-21,158 |
0,059 |
-3,348 |
-90,000 |
-117,597 |
|
1 |
0 |
0,060 |
-3,434 |
0,430 |
-23,269 |
0,065 |
-3,719 |
-90,000 |
-120,423 |
|
2 |
0 |
0,120 |
-6,843 |
0,860 |
-40,699 |
0,130 |
-7,407 |
-90,000 |
-144,949 |
|
3 |
0 |
0,180 |
-10,205 |
1,290 |
-52,221 |
0,195 |
-11,035 |
-90,000 |
-163,461 |
|
4 |
0 |
0,240 |
-13,497 |
1,720 |
-59,831 |
0,260 |
-14,575 |
-90,000 |
-177,903 |
|
5 |
0 |
0,300 |
-16,700 |
2,150 |
-65,061 |
0,325 |
-18,005 |
-90,000 |
-189,767 |
|
6 |
0 |
0,360 |
-19,800 |
2,580 |
-68,819 |
0,390 |
-21,307 |
-90,000 |
-199,927 |
|
7 |
0 |
0,420 |
-22,784 |
3,010 |
-71,627 |
0,455 |
-24,467 |
-90,000 |
-208,879 |
|
8 |
0 |
0,480 |
-25,643 |
3,440 |
-73,796 |
0,520 |
-27,476 |
-90,000 |
-216,916 |
|
9 |
0 |
0,540 |
-28,371 |
3,870 |
-75,517 |
0,585 |
-30,330 |
-90,000 |
-224,218 |
|
10 |
0 |
0,600 |
-30,966 |
4,300 |
-76,914 |
0,650 |
-33,026 |
-90,000 |
-230,906 |
|
14 |
0 |
0,840 |
-40,033 |
6,020 |
-80,574 |
0,910 |
-42,305 |
-90,000 |
-252,913 |
|
15 |
0 |
0,900 |
-41,990 |
6,450 |
-81,193 |
0,975 |
-44,278 |
-90,000 |
-257,461 |
|
16 |
0 |
0,960 |
-43,834 |
6,880 |
-81,736 |
1,040 |
-46,127 |
-90,000 |
-261,697 |
|
20 |
0 |
1,200 |
-50,198 |
8,600 |
-83,374 |
1,300 |
-52,435 |
-90,000 |
-276,007 |
|
30 |
0 |
1,800 |
-60,950 |
12,900 |
-85,574 |
1,950 |
-62,855 |
-90,000 |
-299,378 |
|
40 |
0 |
2,400 |
-67,385 |
17,200 |
-86,679 |
2,600 |
-68,968 |
-90,000 |
-313,032 |
|
50 |
0 |
3,000 |
-71,570 |
21,500 |
-87,343 |
3,250 |
-72,903 |
-90,000 |
-321,816 |
|
60 |
0 |
3,600 |
-74,481 |
25,800 |
-87,787 |
3,900 |
-75,624 |
-90,000 |
-327,892 |
|
70 |
0 |
4,200 |
-76,613 |
30,100 |
-88,104 |
4,550 |
-77,610 |
-90,000 |
-332,327 |
|
80 |
0 |
4,800 |
-78,237 |
34,400 |
-88,341 |
5,200 |
-79,120 |
-90,000 |
-335,699 |
|
90 |
0 |
5,400 |
-79,514 |
38,700 |
-88,526 |
5,850 |
-80,306 |
-90,000 |
-338,346 |
|
100 |
0 |
6,000 |
-80,544 |
43,000 |
-88,674 |
6,500 |
-81,260 |
-90,000 |
-340,478 |
|
200 |
0 |
12,000 |
-85,243 |
86,000 |
-89,340 |
13,000 |
-85,608 |
-90,000 |
-350,191 |
Результаты вычислений отобразим на графике логарифмических характеристик разомкнутой системы:
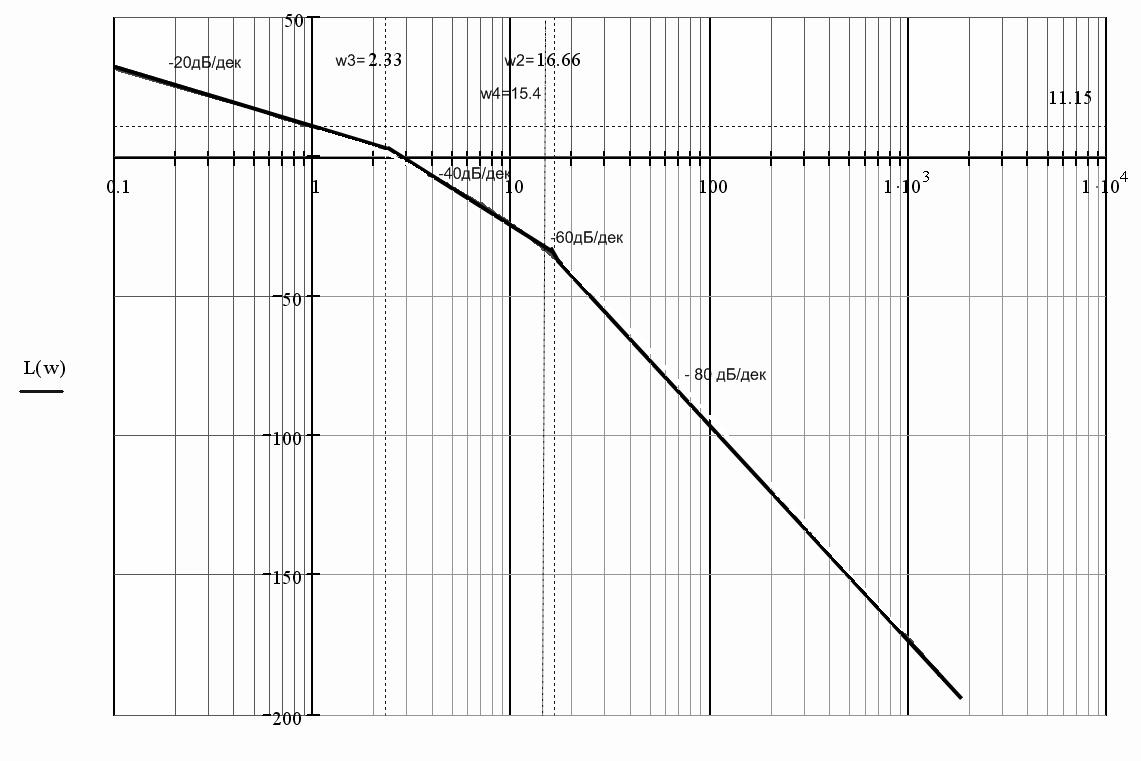
Рисунок 5 – ЛАЧХ разомкнутой системы
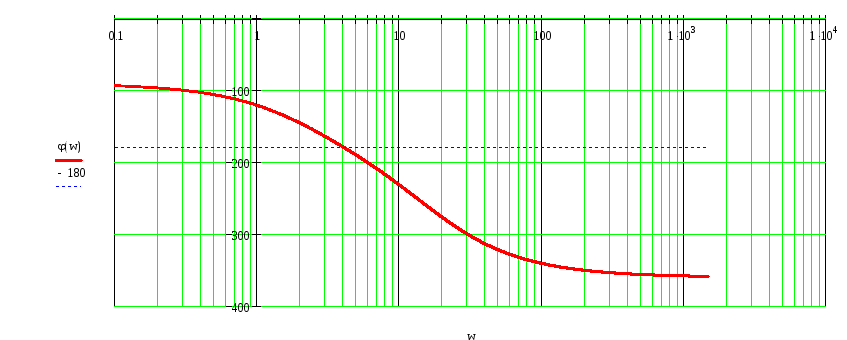
Рисунок 6 – ЛФЧХ разомкнутой системы
Если разомкнутая система устойчива, для ее устойчивости в замкнутом состоянии, необходимо и достаточно, чтобы число переходов ЛФЧХ через линию –180° при положительных значениях ЛАЧХ было четным (в частном случае равным нулю).
В данном случае ЛФЧХ не совершает отрицательных переходов при положительных значениях ЛАЧХ. Можно сделать вывод о том, что замкнутая система будет устойчивой.
Из графиков находим,
что L(2.436)=0 дБ, отсюда
![]() .
.
Из графиков находим,
что
![]() ,
отсюда L(4.17)=-8.07 дБ.
,
отсюда L(4.17)=-8.07 дБ.
Следовательно, запас по модулю составляет 8,07 дБ, а запас по фазе равен 26,35°.
