Вывод по линейной части:

Проведя анализ устойчивости системы по критериям устойчивости Гурвица и Найквиста, было определено, что данная система очистки сточных вод в аэротенках устойчивая, так как……… По графику переходной функции видно, что быстродействие системы равно 8,4 с. По графику амплитудно-частотной функции видно, что полоса пропускания сигнала равна 11,72.

2 ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ ЧАСТИ СИСТЕМЫ

2.1 Упрощение структурной схемы системы с нелинейным элементом

Структурная схема с нелинейным элементом имеет вид:

Рисунок – Структурная схема с нелинейным элементом

В данной схеме:

Г

y

рафик, описывающий нелинейный элемент НЭ, приведен на рисунке

2

x

-2

Рисунок - Характеристика нелинейного элемента

Упростим правую часть структурной схемы.

В этой схеме

Внесем звено W₇(p) в цепь ООС и получим :

Разорвем цепь перед нелинейным элементом и получим

В этой цепи можно четко выделить линейную и нелинейную части, введя замену: .Тогда преобразованная структурная схема примет вид:

Насильственно замкнем данную цепь единичной ООС :

Запишем общую передаточную функцию линейной части:

Подставляя значения передаточных функций звеньев, получим:

2.2 Построение фазового портрета

Передаточную функцию можно записать в виде или , подставляя в эту формулу значение передаточной функции, получим:

Приведенную формулу можно записать в виде:

Воспользуемся пакетом MathCad для решения этого дифференциального уравнения. Введем замену pⁱx=y_i и исключим из левой части уравнения производные выше второго полрядка. Получим систему уравнений для участков (-∞;0) и (0;+∞):

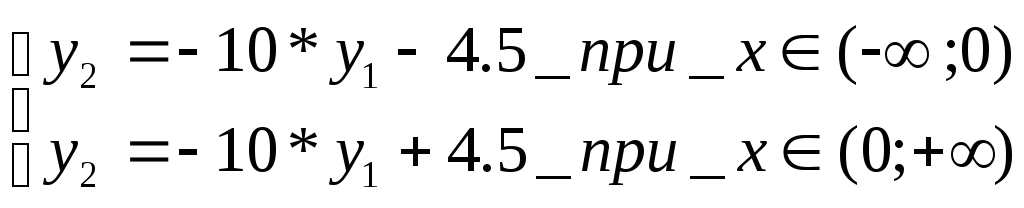
Создадим матрицу для решения дифференциального уравнения:

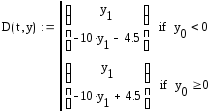
В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицу начальных условий:

Возьмем количество точек равным 10000 и конечное время интегрирования 100, то матрица решений запишется как: .

По введенным данным получим фазовый портрет (рисунок).

Рисунок -

4 Анализ устойчивости

На рисунке 9 представлен фазовый портрет нелинейной системы. Это типовой вид кривой. До перехода через точку -2 работает первое уравнение системы, при переходе через эту точку начинает работать второе уравнение. Третье уравнение работает при переходе через точку 2. Характер фазовой линии такой, что она постоянно приближается к началу координат, т.е. нелинейная система с релейным элементом устойчива. При движении к состоянию устойчивости амплитуда колебаний постоянно уменьшается, а частота переключения растет. Получаем, что амплитуда колебаний в итоге примет нулевое значение, а частота колебаний станет бесконечно большой.