1 ИССЛЕДОВАНИЕ ЛИНЕЙНОЙ ЧАСТИ СИСТЕМЫ

1.1 Принцип работы системы

Д

3

ля выполнения курсовой работы мной была выбрана технологическая схема очистки сточных вод в аэротенках, которая приведена на рисунке 1.

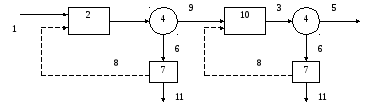
1. подача неочищенных сточных вод; 2 - аэротенк;

3 - выпуск иловой смеси;

4- отстойник; 5- выпуск очищенных сточных вод;

6- выпуск отстоенного активного ила; 7- иловая насосная станция;

8- подача возвратного активного ила; 9- выпуск сточных вод

после первой ступени очистки; 10- аэротенк 2-ой ступени;

11- выпуск избыточного активного ила.

Рисунок 1 - Технологическая схема очистки сточных вод в аэротенках

Принцип действия данной системы состоит в том, что сточная вода поступает в аэротенк, где она смешивается с илом и насыщается воздухом. Затем получившаяся иловая смесь поступает в отстойник, где происходит отделение воды от ила. С помощью насоса из отстойника откачивается активный ил и происходит выпуск избыточного активного ила. Так как система является двухступенчатой, то данный процесс повторяется, после чего происходит выпуск очищенных сточных вод.

1.2 Построение принципиальной схемы

Рисунок 2 – Принципиальная схема

С учётом значений давления в различных элементах системы получим следующую принципиальную схему:

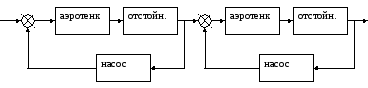
Рисунок 3 – Принципиальная схема со значениями давлений

1.3 Построение структурной схемы

Для построения структурной схемы определим передаточные функции всех элементов системы. Передаточная функция является математической моделью системы в виде вход – выход. Так как аэротенк и отстойник являются ёмкостями, то их передаточная функция будет определяться в виде: ,

где k – коэффициент передачи, рассчитывается по формуле: ;

T – постоянная времени, рассчитывается по формуле: . В ходе курсовой работы примем значение постоянной времени, равное .

Так как на входе первого аэротенка величина давления равна , а на выходе - , то коэффициент передачи будет равен: k₁=480/500=0.96, тогда T₁=0,05k₁=0,048. В итоге передаточная функция первого аэротенка будет равна: .

Так как на входе второго аэротенка величина давления равна , а на выходе - , то коэффициент передачи будет равен: k₄=380/400=0.95, тогда T₄=0,048. В итоге передаточная функция второго аэротенка будет равна: .

Так как на входе первого отстойника величина давления равна , а на выходе - , то коэффициент передачи будет равен: k₂=450/480=0.94, тогда T₂=0,05k₂=0,047. В итоге передаточная функция первого отстойника будет равна: .

Так как на входе второго отстойника величина давления равна , а на выходе - , то коэффициент передачи будет равен: k₅=350/380=0.92, тогда T₅=0,05k₅₌0,046. В итоге передаточная функция второго отстойника будет равна: .

Передаточная функция насоса определяется по выражению:

,

где k – коэффициент передачи ;

T – постоянная времени: . В ходе курсовой работы примем значение постоянной времени, равное .

Так как на входе первого насоса величина давления равна , а на выходе - , то коэффициент передачи будет равен: k₃=25/100=0.25, тогда T₃=0,05k₃=0,013. В итоге передаточная функция первого насоса будет равна: .

Так как на входе второго насоса величина давления равна , а на выходе - , то коэффициент передачи будет равен: k₆=50/100=0.5, тогда T₆=0,05k₆=0,025. В итоге передаточная функция первого насоса будет равна: .

В итоге получаем следующую структурную схему:

Рисунок 4 – Структурная схема системы

1.4 Определение устойчивости системы по критерию устойчивости Гурвица.

Этот критерий формирует условие устойчивости в виде определителя.

Для характеристического уравнения L(p) составляют определитель, содержащий n строк и n столбцов:

По диагонали от левого верхнего до правого нижнего углов вписываются все коэффициенты по порядку от а₁ до a_n. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. В случае отсутствия данного коэффициента, а также если индекс его меньше нуля или больше n, на месте его пишется нуль. Из главного определителя выделяются диагональные миноры:

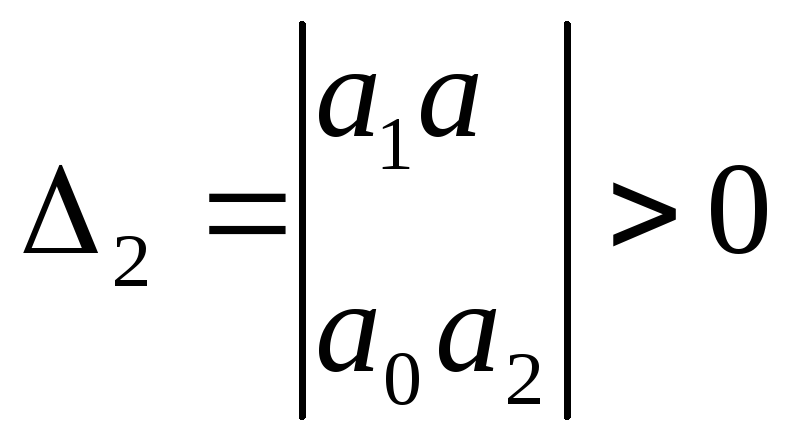
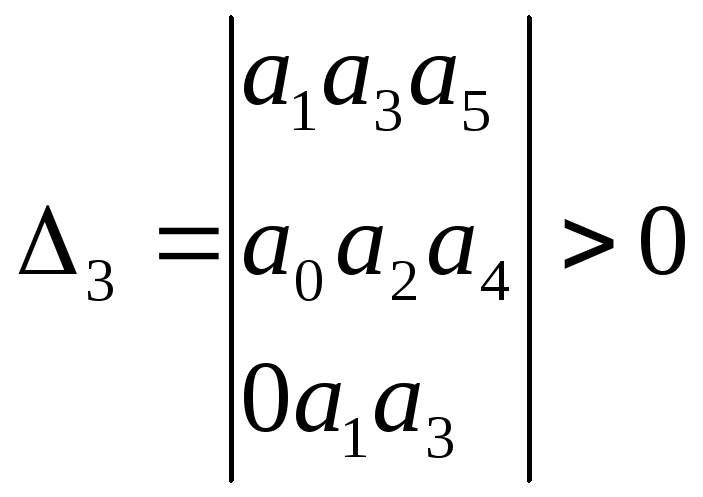
Критерий устойчивости Гурвица заключается в следующем:

чтобы характеристическое уравнение имело все корни с отрицательной вещественной частью, главный определитель и все диагональные миноры должны иметь значения, большие нуля.

Для того, чтобы определить выражение для характеристического уравнения определим выражение для общей передаточной функции. Используя правила преобразования структурных схем, получим:

Подставляя значения передаточных функций звеньев, получим:

Запишем выражение для характеристического уравнения:

Все коэффициенты характеристического уравнения положительны, значит, необходимое условие устойчивости выполняется.

Составим определитель Гурвица:

Определим значения миноров:

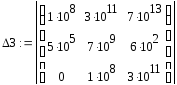
Вывод об устойчивости:

Все миноры определителя Гурвица положительны, значит, вещественная часть корней характеристического уравнения отрицательна, и система автоматического управления устойчива.

1.5 Определение устойчивости системы по критерию устойчивости Найквиста.

Критерий Найквиста позволяет по годографу амплитудной фазовой характеристики системы судить об устойчивости замкнутой системы. Годограф имеет действительную и мнимую оси, на которых откладываются соответственно действительные и мнимые значения передаточной функции в зависимости от частоты. Критерий Найквиста можно сформулировать следующим образом: САР, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если годограф не охватывает точку (-1, j0). В противном случае, при неустойчивости системы, годограф охватывает эту точку в положительном направлении раз, где p – количество корней.

Для этого в выражении для Wобщ(p) заменим p на jw.

Определим действительную U(w) и мнимую части V(w) передаточной функции. Для этого необходимо умножить числитель и знаменатель выражения W(w) на сопряженное знаменателю выражение. В итоге получим выражение:

Выражения для действительной и мнимой частей соответственно:

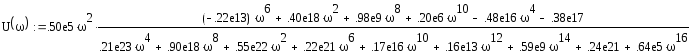
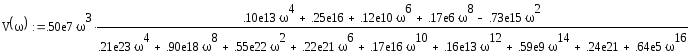
Построим зависимость V(w) от U(w), чтобы определить устойчивость системы.

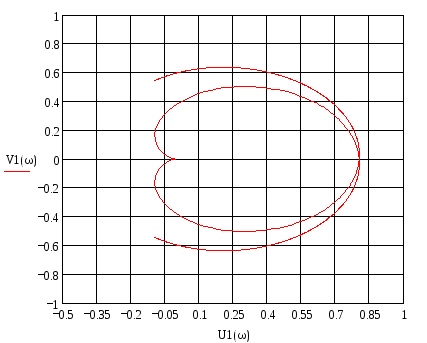
Рисунок – Годограф ………

На графике видно, что годограф не охватывает точку (-1;j0). Это означает, что система устойчивая.

1.6 Построение переходного процесса.

Он определяется как обратное преобразование Лапласа от W(p)/p. Тогда получим

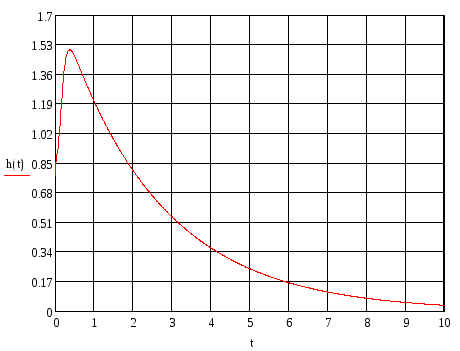
Рисунок – График переходного процесса системы

По графику переходного процесса определим все характеристики системы.

h_max=1,53 h_уст=0 t_max=0,3 t_p=8,4 t_согл=9,5

Перерегулирование равно. Так как h_уст=0 , то определить перерегулирование для данной системы не допустимо.

6) Построим амплитудно-частотную характеристику.

АЧХ определяется по выражению

Подставив ранее рассчитанные выражения для U(w) и V(w), получим

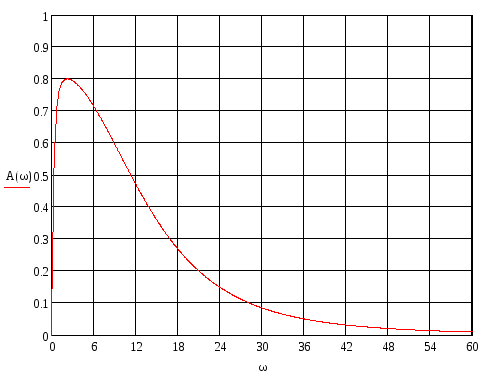
Рисунок – График амплитудно-частотной характеристики системы

По графику определим следующие характеристики:

Amax=0,55 A(0)=0 A=0,7Amax=0,38

Полоса пропускания сигнала равна ( ),

то есть равна 11,72.

Показатель колебательности