курсовая работа / Линейная часть_Nat

1. Линейная часть.

   1. Упростим систему.

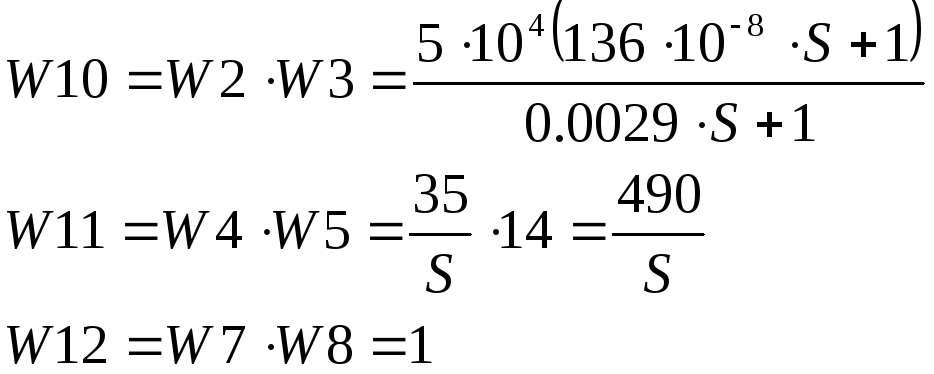
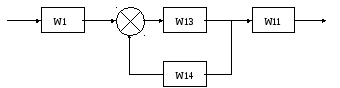
Тогда структурная схема будет выглядеть следующим образом:

Объединим W6 c W12 и W10 c W12:

Структурная схема примет вид:

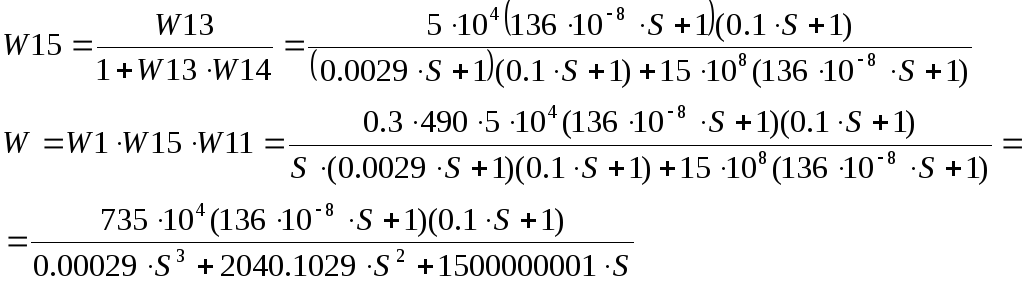
2. Определим устойчивость системы.

Воспользуемся критерием устойчивости Ляпунова. Для этого найдем корни характеристического полинома полученной передаточной функции.

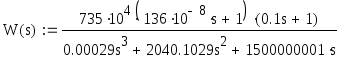
Так как в результате получили два отрицательных корня и один нулевой, то, согласно критерию Ляпунова, можно сделать вывод, что система находится на границе апериодической устойчивости.

Передаточную функцию можно записать следующим образом:

или

3. Построим переходный процесс системы.

Переходная функция- это реакция системы на единичное ступенчатое воздейст-

вие.

, где W1(s)- передаточная функция замкнутой системы, которая определяется по формуле:

Тогда

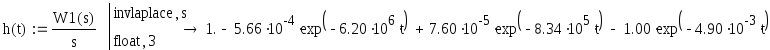
Построим график переходного процесса.

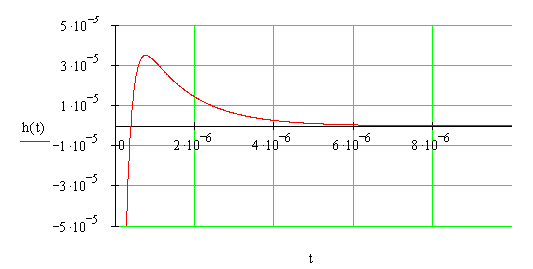
По виду графика переходного процесса также можно сделать вывод, что система устойчивая.

1.4 Построим АЧХ и ФЧХ системы.

Перейдем к частотной форме записи передаточной функции разомкнутой системы. Для этого заменим , получим:

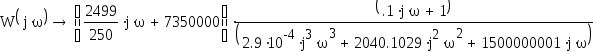где - мнимая единица;

Определим действительную и мнимую часть.

Найдем АЧХ системы по формуле:

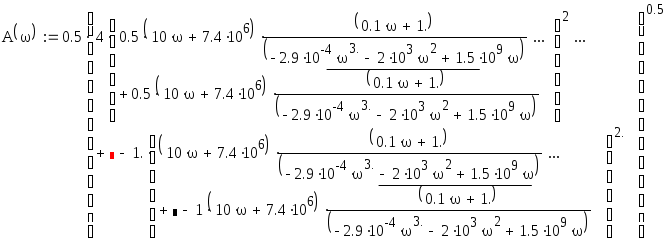
Построим график АЧХ.

Найдем ФЧХ системы по формуле:

или

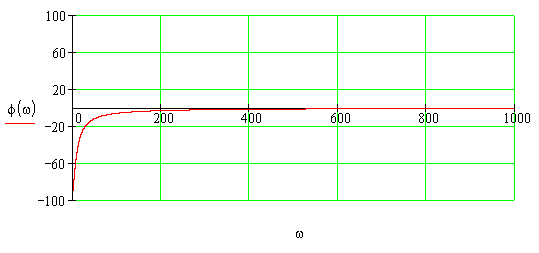
1.5 Построим ЛАЧХ и ЛФЧХ.

Определим собственные частоты каждого звена данной передаточной функции:

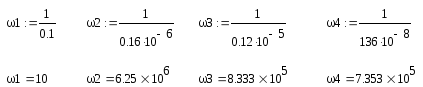
График ЛАЧХ будет иметь вид:

Построим график ЛФЧХ