Задание по контрольной работе № 1

по дисциплине

«Вычислительная математика»

Методические рекомендации по выполнению контрольной работы

Выполнение заданий требует проведения расчетов. Отчет о выполнении работы должен содержать все промежуточные вычисления при выполнении расчетов, пояснения к вычислениям, краткое описание хода решения задачи и изложение сути применяемых методов, а также распечатка файлов в формате Excel с решением задач при решении в Пакете, сами файлы приносятся на итоговый контроль.

В качестве методических пособий при выполнении работы, которые содержат множество примеров решения задач данного типа, рекомендуются издания, указанные в списке литературы.

Контрольная работа оформляется в соответствии с требованиями «Общих методических указаний по выполнению и оформлению домашней контрольной работы студентами-заочниками».

Вариант контрольной работы определяется номером в журнале задания для контрольной работы Вариант 1

1. На отрезке [0; 2] методом бинарного деления найти корень уравнения с точностью 0,1. Для решения задачи предварительно построить график функции и выполнить отделение корней.

2. Методом секущих найти отрицательный корень уравнения 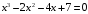с точностью 0,1. Для решения задачи предварительно построить график функции и выполнить отделение корней.

3. Определить значения корней системы уравнений методом Гаусса

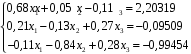
4. Численно определить значение производной функции 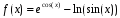при x=0.69 с точностью до третьего знака после запятой.

5. Численно определить значение второй производной функции 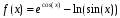при x=0.69 с точностью до третьего знака после запятой.

6. Методом правых прямоугольников вычислить интеграл 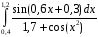с шагом 0.02.

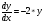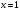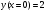7. Методом Эйлера определить решение дифференциального уравнения в точке . начальные условия . Шаг интегрирования 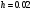. (ЭТ):

8. Дана таблица значений функции. Методом квадратичной интерполяции вычислить значение функции при x=0,15

x	y
0,00	1,000
0,10	1,095
0,20	1,179

9. Вычислить абсолютную погрешность, если относительная погрешность результата 10%, если приближенное значение равно 5 и превышает точное значение.

10. Определить относительную погрешность, если точное значение корня равно 5, а приближенное значение равно 6.

Вариант 2

1. На отрезке [0; 2] методом Ньютона найти корень уравнения 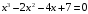с точностью 0,1. Для решения задачи предварительно построить график функции и выполнить отделение корней.

2. Методом бинарного деления найти отрицательный корень уравнения 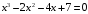с точностью 0,1. Требуется предварительное построение графика функции и отделение корней.

3. Определить значения корней системы уравнений методом Гаусса

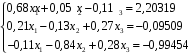
4. Вычислить абсолютную погрешность, если точное значение корня равно 6, приближенное значение равно 7.

5. Определить относительную погрешность для предыдущего примера.

6. Численно определить значение производной функции 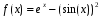при x=2,75 с точностью до второго знака после запятой. (ЭТ) Требуется построение таблицы функции.

7. Численно определить значение второй производной функции 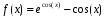при x=-1.65 с точностью до второго знака после запятой. Требуется построение таблицы функции.

8. Методом трапеций вычислить интеграл 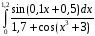с шагом 0.01.

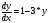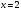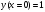9. Методом Эйлера определить решение дифференциального уравнения в точке . начальные условия . Шаг интегрирования .

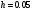10. Дана таблица значений функции. Используя интерполяционный многочлен Лагранжа второй степени вычислить значение функции при x=0,277.

x	y
0,00	1,000
0,20	1,179
0,40	1,310