лекции / увц / 4

3.3. Временные характеристики

Временные характеристики показывают закон изменения во времени регулируемой (выходной) величины САУ (элемента) при изменении внешнего воздействия по определенному закону и при нулевых начальных условиях. Временные характеристики отражают динамические свойства САУ (элементов), которые могут быть определены по переходной функции (характеристике) и по импульсной переходной характеристике (функции веса).

Переходная характеристика (функция) h(t) представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице, или реакцию системы (элемента) на входной сигнал в виде единичной ступенчатой функции (рис. 3.8).

Переходная характеристика может быть определена экспериментально или аналитически. При аналитическом определении переходной характери-стики нужно найти решение дифференциального уравнения САУ (элемента) при входном сигнале Х_вх(t) =1(t) и нулевых начальных условиях.

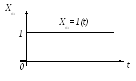
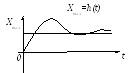
Рис. 3.8. Переходная характеристика

Переходная характеристика обычно представляется в виде графика. Конкретные очертания характеристики h(t) зависят от динамических свойств САУ (элемента) и могут быть весьма разнообразными.

Если входное воздействие представляет собой не единичную ступенчатую функцию , то выходная величина будет равна , где N=const. Более строго переходную характеристику можно определить как отношение выходной величины звена к высоте N ступенчатого скачка на его входе, т. е.

, (3.12)

Функция веса, или импульсная переходная характеристика , пред-ставляет собой реакцию САУ (элемента) на единичную импульсную функ-цию, поданную на ее вход. На рис. 3.9. показаны возможные виды импуль-сных переходных характеристик. Вид их зависит от динамических свойств САУ (элемента).

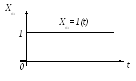
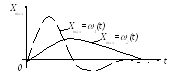
Рис. 3.9. Импульсная переходная характеристика

Нетрудно установить связь между переходной функцией и функцией веса. Рассмотрим входное воздействие звена в виде конечного по высоте и ширине импульса с площадью , прикладываемого при t=0 (рис.3.9).Такой импульс может быть заменен двумя ступенчатыми функциями: и , прикладываемыми к входу звена со сдвигом во времени . Тогда выходная величина звена будет равна

. (3.13)

Будем теперь увеличивать высоту импульса N, одновременно уменьшая

его ширину , так, чтобы все время площадь импульса равнялась единице:

. Помножив и поделив правую часть равенства (3.13) на  и перейдя к

пределу, получим функцию веса

.

Таким образом, импульсная переходная характеристика может быть по-

лучена дифференцированием по времени переходной характеристики:

. (3.14)

При исследовании динамических свойств САУ (элементов) чаще используют переходную характеристику, ее удобно использовать при оценке качества переходного процесса в САУ.

Частотные характеристики

Как и временные характеристики, частотные характеристики широко используются при исследовании динамических свойств САУ и их элементов. Частотные характеристики САУ определяют зависимость между входной и выходной величинами в установившемся режиме при гармоническом воздействии.

Частотные характеристики лежат в основе частотных методов исследования САУ, которые получили широкое распространение благодаря их наглядности и сравнительной простоте. Они позволяют не только исследовать свойства системы в установившемся режиме, но и судить об устойчивости системы, оценить качество процесса управления.

Важнейшей характеристикой динамического звена является его частотная передаточная функция. Для получения ее рассмотрим динамическое звено в случае, когда возмущение f(t)=0, а на входе имеется гармоническое воздействие

, (3.15)

где А_вх – амплитуда входного воздействия;  - круговая частота (0<  <).

По окончании переходного процесса на выходе САУ (элемента) будут существовать гармонические колебания с той же частотой, что и входные колебания, но отличающиеся в общем случае по амплитуде и фазе, т. е. в установившемся режиме

(3.16)

где А_вых – амплитуда выходных колебаний;  - фазовый сдвиг между входными и выходными колебаниями (рис. 3.10).

Х

X_вх(t)

X_вых(t)

A_вх

t

A_вых



Рис. 3.10. Входные и выходные колебания в САУ

При фиксированной амплитуде входных колебаний амплитуда и фаза установившихся колебаний на выходе зависят от частоты колебаний. Если постепенно увеличивать от нуля частоту колебаний и определять установившиеся значения амплитуды и фазы выходных колебаний для разных частот, можно получить зависимость от частоты отношения амплитуд:

(3.17)

и сдвига фаз () выходных и входных установившихся колебаний от частоты. Эти зависимости определяются соответственно:

А() – амплитудно-частотная характеристика (АЧХ);

() – фазочастотная характеристика (ФЧХ).

Примерный вид этих характеристик для инерционных элементов (звеньев) изображен на рис. 3.11. Как показано на рисунке, АЧХ по мере увеличения частоты стремится к 0, ФЧХ отрицательная, то есть выходные колебания отстают по фазе от входных, и это отставание растет с частотой.

Рассмотренные частотные характеристики могут быть получены экспериментально или аналитически. Аналитические выражения для частотных характеристик легко получаются по передаточной функции. Если в выражение передаточной функции подставить , то получится комплексная передаточная функция :

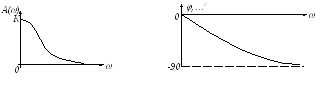
Рис. 3.11. АЧХ и ФЧХ инерционного звена

Комплексная передаточная функция является амплитудно-фазовой частотной характеристикой (АФЧХ) и представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной или АЧХ, а аргумент – сдвигу фаз выходной величины по отношению к входной или ФЧХ:

(3.18)

(3.19)

Так, например, для электрического контура (рис. 3.1), имеющего передаточную функцию:

,

комплексная передаточная функция АФЧХ имеет вид

амплитудно-частотная характеристика

,

фазочастотная характеристика:

Графики и рассматриваемого контура представлены на рис. 3.11.

Комплексная передаточная функция может быть представлена в пока-

зательной форме:

(3.20)

или в алгебраической

, (3.21)

где – вещественная частотная характеристика; – мнимая частотная характеристика.

Амплитудно-фазовая частотная характеристика строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции (3.21) при изменении частоты от 0 до  (рис. 3.12). По оси абсцисс откладывается веществен­ная часть и по оси ординат – мнимая часть . Для каждой час­тоты на комплексной плоскости наносится точка. Полученные точки соединяются затем плавной кри­вой.

Для оценки динамических свойств САУ и их элементов АЧХ и ФЧХ обычно строят в логарифмических координатах.

Прологарифмируем выражение частотной передаточной функции (3.20):

.

Как видно из этого выражения, логарифм частотной передаточной функ­ции равен комплексному выражению, вещественной частью которого являет­ся логарифм модуля, а мнимой – фаза. Для практических целей удобнее пользоваться десятичными логарифмами и строить отдельно логарифмическую амплитудную частотную харак­теристику (ЛАЧХ) и логарифмическую фазовую частотную характеристику (ЛФЧХ). Для построения ЛАЧХ находится величина

. (3.22)

Эта величина выражается в децибелах [дБ]. Бел представляет собой логарифми­ческую единицу, соответствующую десятикратному увеличению мощности. Один бел соответствует увеличению мощности в 10 раз, 2 бела – в 100 раз, 3 бела – в 1000 раз и т. д. Децибел равен одной десятой части бела.

На оси абсцисс откладывают десятичные догарифмы частоты или значения самой частоты в логарифмическом масштабе (см. рис. выше). На практике наиболее распространен второй способ, при котором шкала будет не равномерной (логарифмическая шкала). Отрезок этой шкалы, соответствующий изменению частоты в 10 раз называется декадой. Точка находится слева в бесконечности, так как . Оцифровка оси частот зависит от требуемого диапазона частот для анализа САУ. При построении ЛФЧХ используется та же ось частот, что и при построении ЛАЧХ.