лекции / В. А. Бородавкин, И. Л. Петрова -ТАУ дискретных систем / 3 Лекция

7

3 Лекция

Математические основы дискретных систем

Поскольку значения решетчатой функции известны только для дискретных значений аргумента,то для изучения поведения таких функций методы дифференциального и интегрального исчисления оказываются непригодными. Для оценки свойств решетчатой функции используется аппарат конечных разностей и конечных сумм, позволяющий оценивать свойства числовых последовательностей (функций дискретного аргумента). Для исследования динамики дискретных импульсных СУ используются разностные уравнения. Их решение, так же как и дифференциальных, представляет известные трудности. В связи с этим, в теории дискретных (импульсных) САУ широко используются операционные методы.

3.1 Z – преобразование. Модифицированное Z – преобразование. Обратное Z – преобразование.

Метод Z – преобразования нашел широкое применение при исследовании импульсных и цифровых систем управления. Если поведение системы достаточно полно описывается только в дискретные моменты времени, то наиболее удобным математическим аппаратом для анализа и синтеза является аналог преобразования Лапласа – дискретное преобразование Лапласа или т.н. Z – преобразование.

Z – преобразованием решетчатой функции называется функция комплексного аргумента Z, определяемая выражением

, (1)

Это выражение может быть получено следующим образом. Если предыстория системы относительно учитывается соответствующими граничными условиями, то допустимо полагать, что непрерывная функция времени при t<0. В этом случае, как известно, функция может быть заменена изображением по Лапласу (одностороннее преобразование)

(2)

Взяв конечный интервал времени равным периоду дискретности () и представив текущее время в виде последовательности можно в выражении (2) интеграл заменить суммой, а величину dt периодом квантования :

. (3)

Выражение (3) представляет собой дискретное преобразование Лапласа. Предел этого выражения при даст преобразование Лапласа непрерывной величины (2).

Если обозначить , то

(4)

(Обозначив )

Комплексное

переменное

При этом Z-преобразование, как следует из формулы (1), отличается от дискретного преобразования Лапласа только множителем Т, т.е.

.

Итак, преобразование Лапласа для дискретной функции привело к бесконечной сумме. Бесконечная сумма является функцией комплексного переменного .

Операция суммирования носит название прямого дискретного преобразования Лапласа (или Z-преобразования) для решетчатой функции в функцию комплексного переменного Z. Эта операция кратко обозначается как И указывает, что есть Z – изображение решетчатой функции или, короче, . Соответственно является оригиналом . Изображение существует, если (1) сходится.

На основе выражения (1) получены таблицы Z-преобразований различных функций времени. В таблице 3.1 приведены выражения Z-преобразований для некоторых функций времени.

Очевидно, что все функции времени, имеющие одинаковые значения в точках t=nT оси времени, обладают одинаковыми Z-преобразованиями . Это означает, что связь между функцией времени и соответствующим ей Z-преобразованием не является взаимно однозначной. Функция характеризует только последовательность чисел , но не позволяет судить о поведении оригинала внутри интервалов.

Таблица 3.1

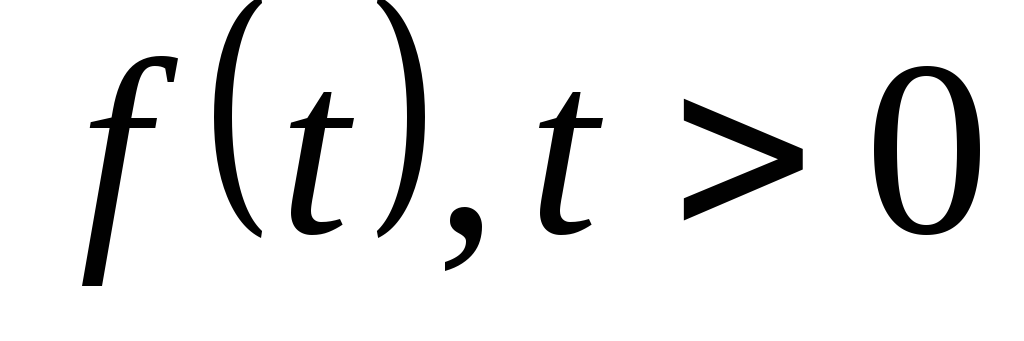
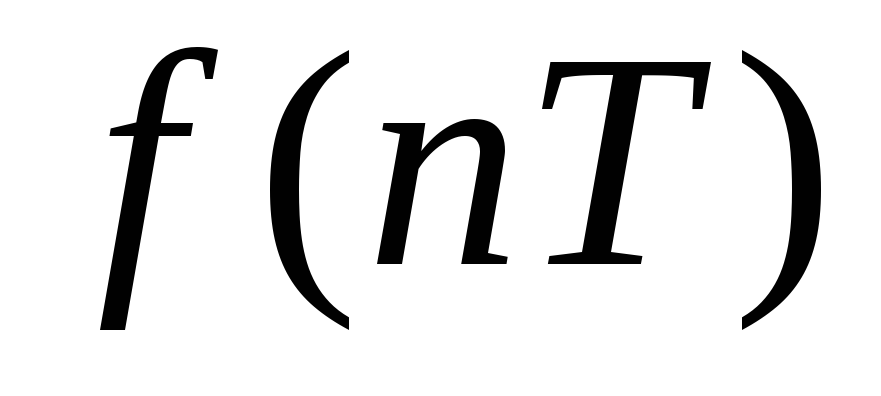
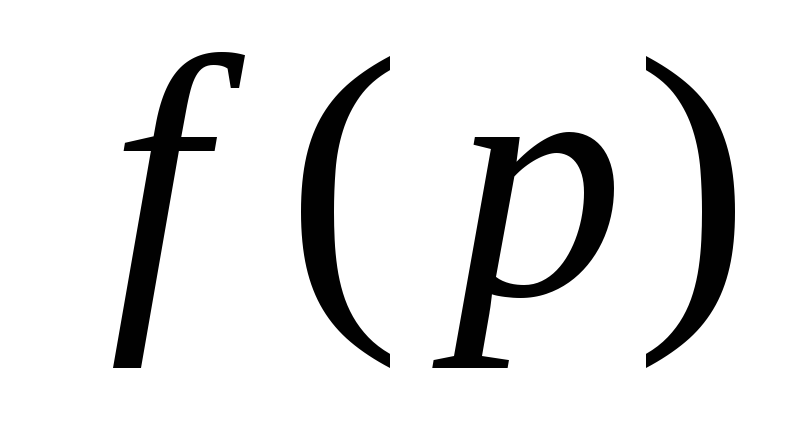
		Изображение по Лапласу	Z-изображение
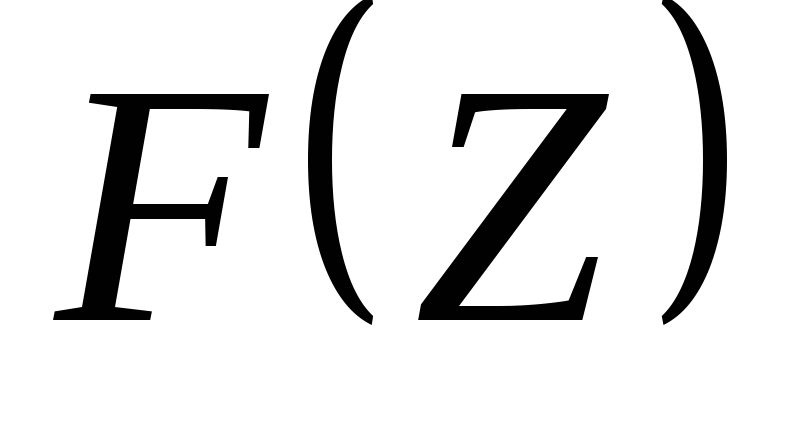
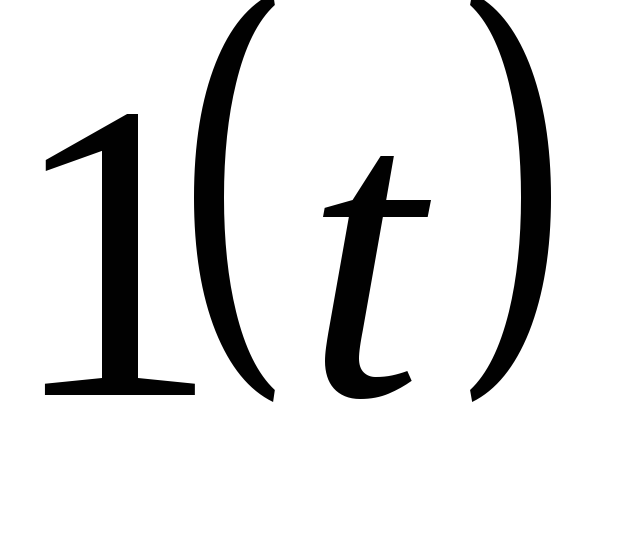
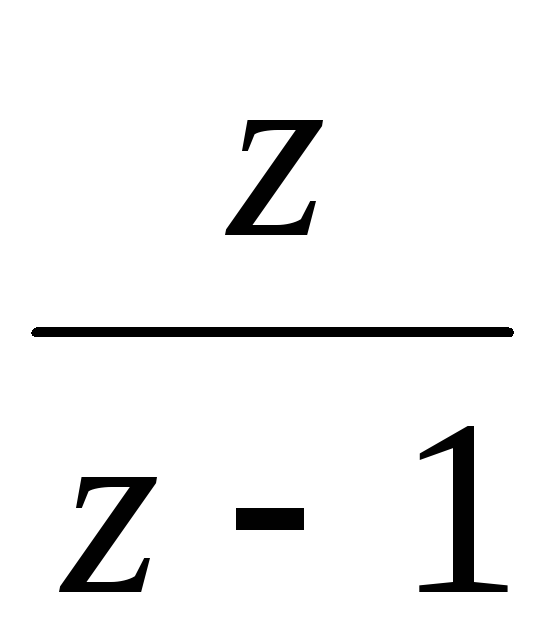
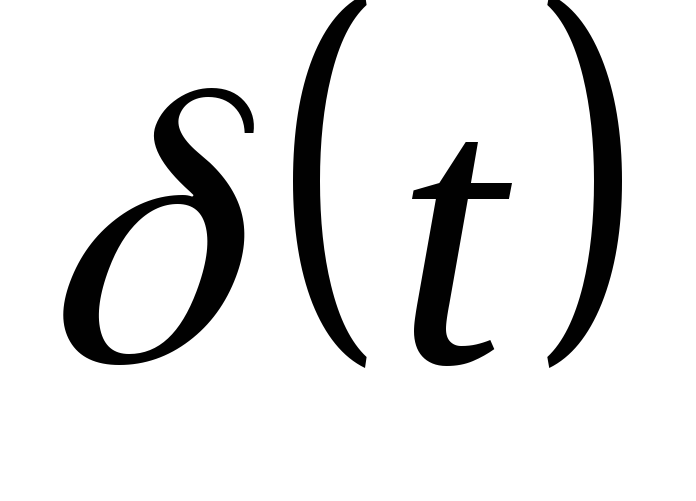
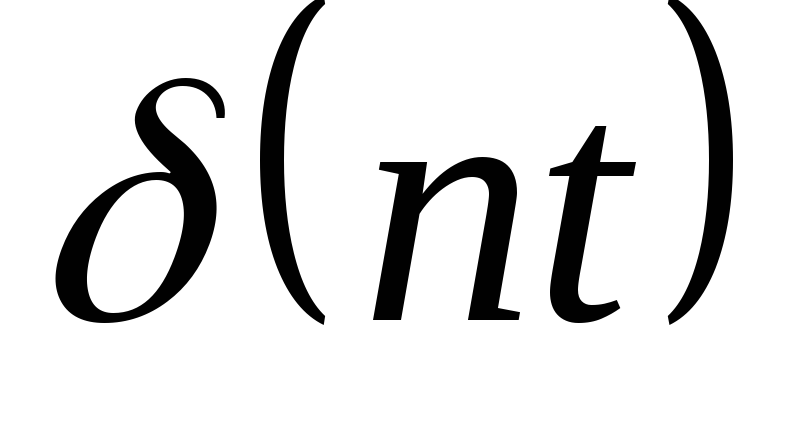
		1	1
t	nT

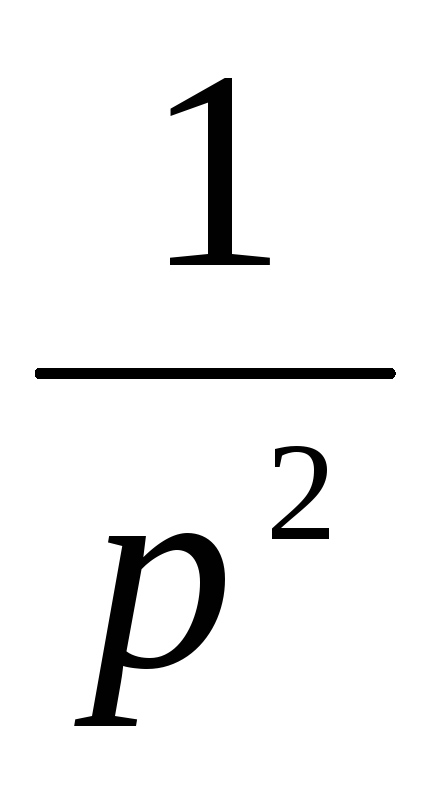
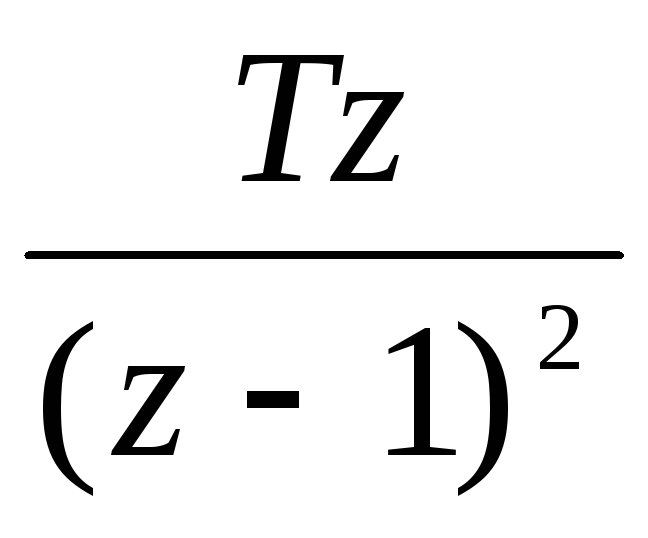
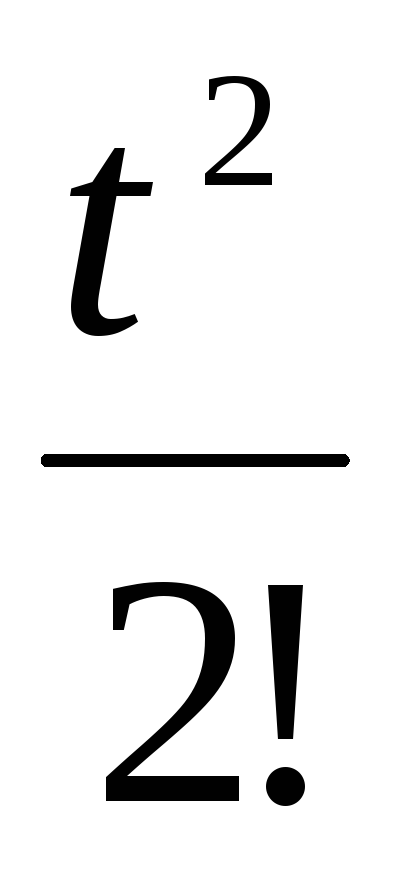
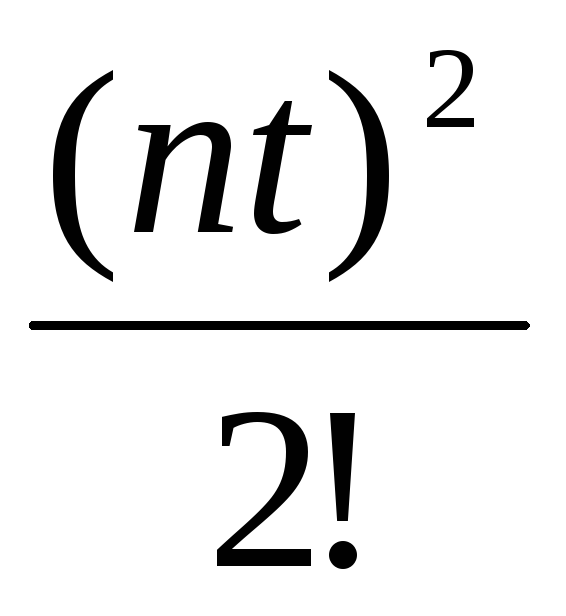
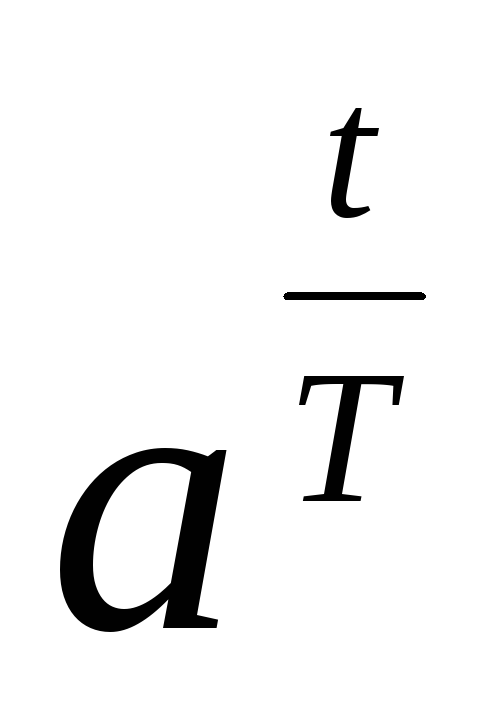
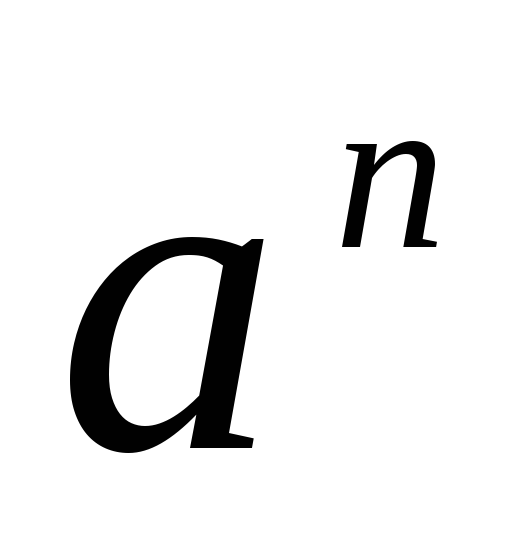
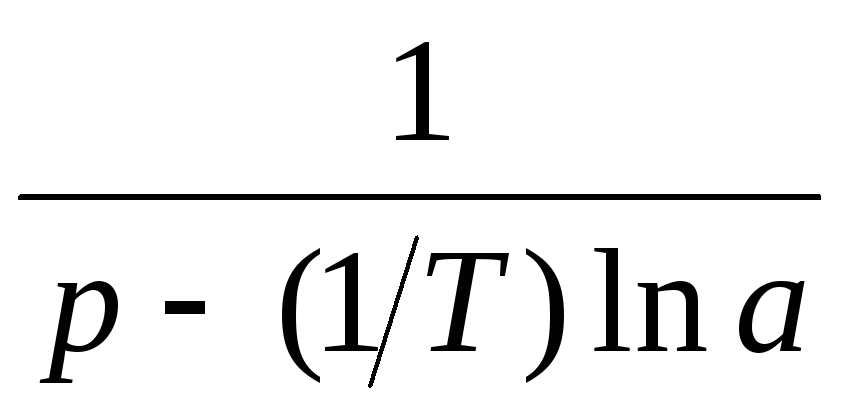
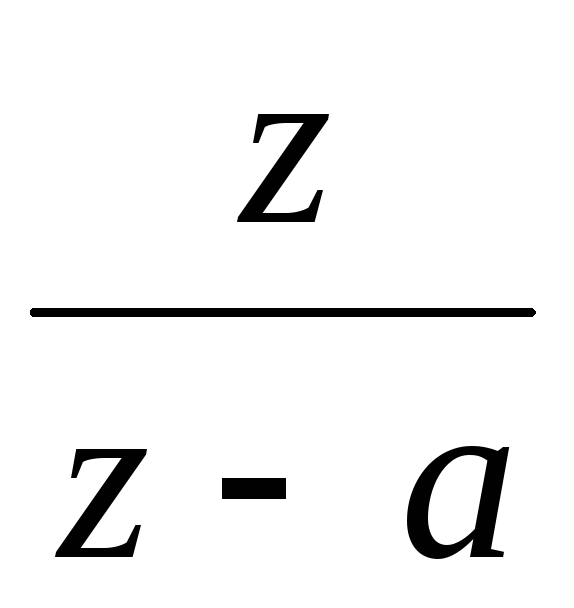
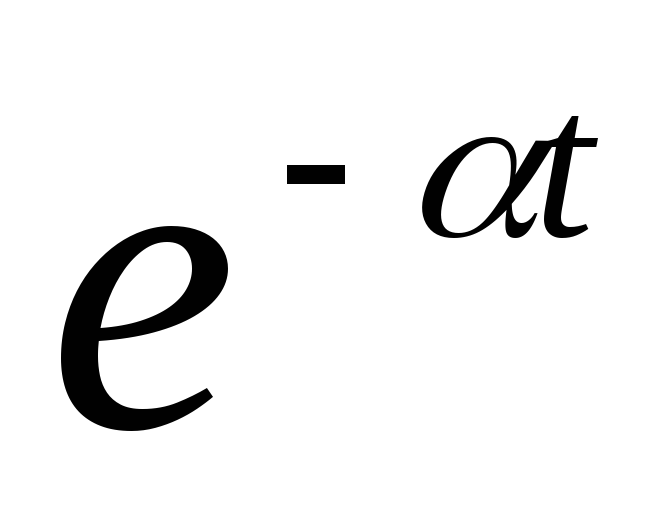
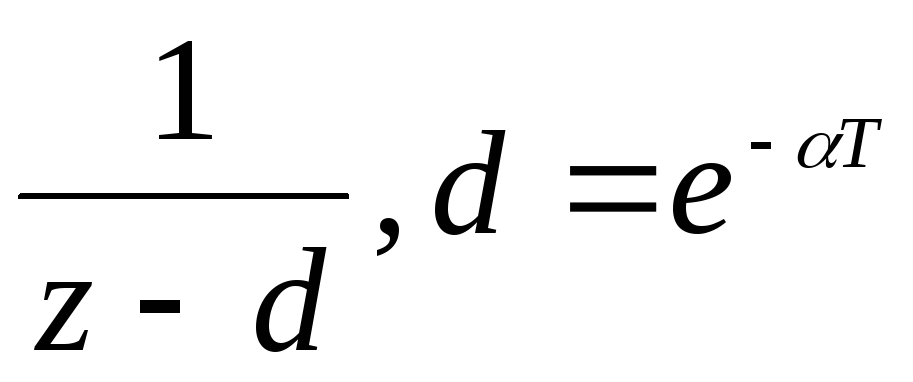
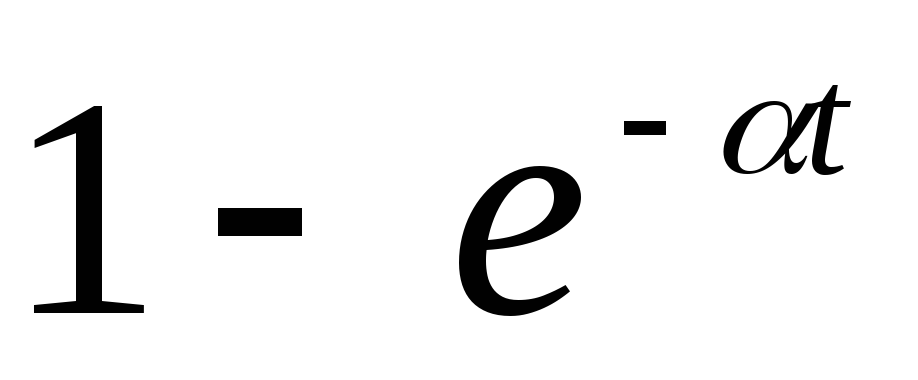
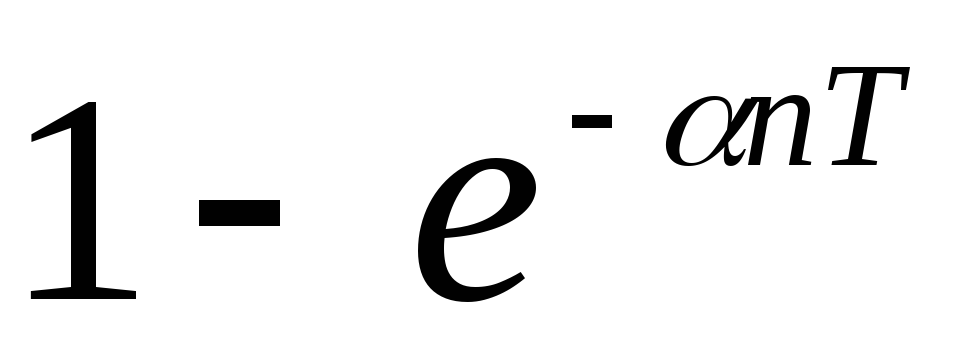
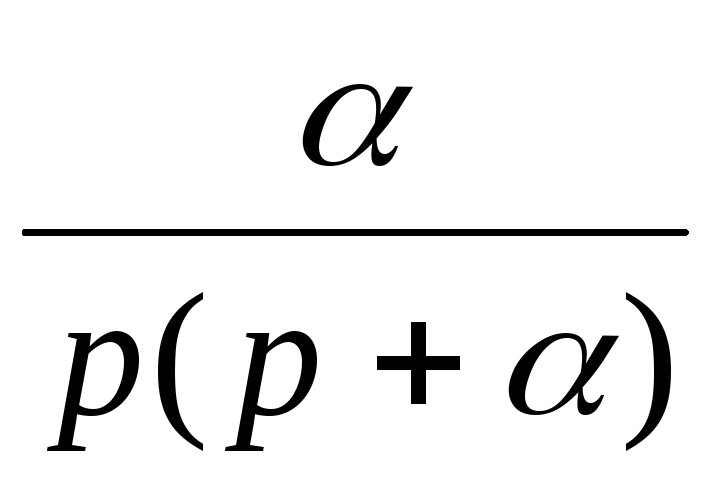
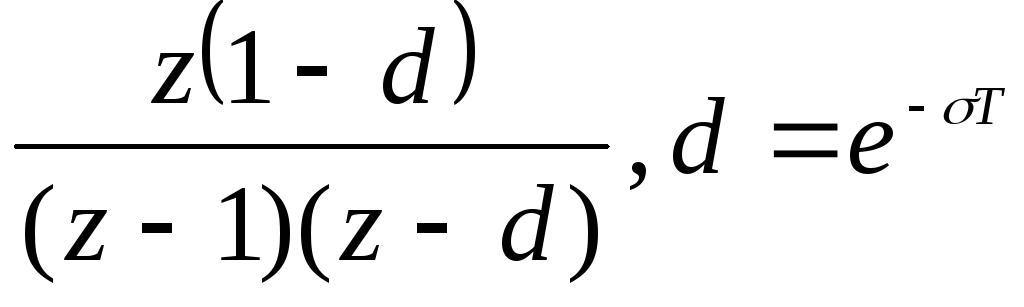
Модифицированное Z-преобразование.

Если значение Z-изображений необходимо знать не только в дискретные моменты времени t=nT, но и в любые другие моменты времени, смещенные на  по отношению к моментам квантования, то можно использовать модифицированное Z-преобразование:

(5)

где  - действительный независимый параметр, принимающий произвольное значение от нуля до единицы. Модифицированное Z-изображение решетчатой функции либо определяется из формулы (5), либо следует использовать таблицы для модифицированного Z-преобразования.

Обратное Z-преобразование позволяет определить решетчатую функцию-оригинал или по ее Z-преобразованию и сокращенно записывается в виде

или

При заданной существует три способа нахождения решетчатой функции: в виде бесконечного ряда, разложением на элементарные дроби и при помощи интеграла обратного преобразования.

Первый метод позволяет непосредственно получить числовую последовательность . Если представляет собой рациональную функцию, т.е. отношение двух многочленов, то разделив многочлен числителя на многочлен знаменателя, получим бесконечный ряд Лорана. Числовые значения коэффициентов членов ряда определяют дискреты решетчатой функции . Указанный способ позволяет определять сколь угодно большое число значений n. При выполнении операции деления многочлены числителя и знаменателя следует записывать по возрастающим степеням ().

Пример 1.

Дано:

Определить:

Решение:

Путем непосредственного деления получим

Отсюда

;

Второй метод основан на разложении функции на элементарные дроби и использовании таблицы преобразования. Непосредственно функция на элементарные дроби не раскладывается, так как фигурирующие в таблице функции от z имеют в числителе множитель z.

Пример 2.

Дано:

Определить:

.

Решение:

Разложим на элементарные дроби:

Из таблицы соответствия получим:

Третий метод нахождения решетчатой функции основан на интеграле обратного преобразования:

или

В этом случае интегрирование ведется по окружности , где с – абсцисса абсолютной сходимости. Окружность, по которой ведется интегрирование, охватывает все особые точки подынтегрального выражения. Формулы обратного преобразования мало применяются.

Использование аппарата Z-преобразования позволило развить теорию линейных дискретных САУ, до некоторой степени аналогичную теории линейных систем непрерывного действия.

3.2 W – преобразование. Определение и свойства.

Для анализа и синтеза непрерывных САУ широко применяется частотный метод, основанный на построении логарифмических частотных характеристик. Простота и наглядность логарифмического частотного метода исследования непрерывных САУ вызывает естественное стремление использовать метод ЛЧХ для анализа и синтеза дискретных систем. Последнее возможно на основе w-преобразования.

Комплексная переменная w связана с комплексной переменной соотношением

(6)

Соотношение заданное в форме (6), получило название w-преобразование. Рассмотрим это преобразование подробнее, для чего запишем его в форме

(7)

изменяя переменную р вдоль мнимой оси плоскости Р т.е. полагая , найдем

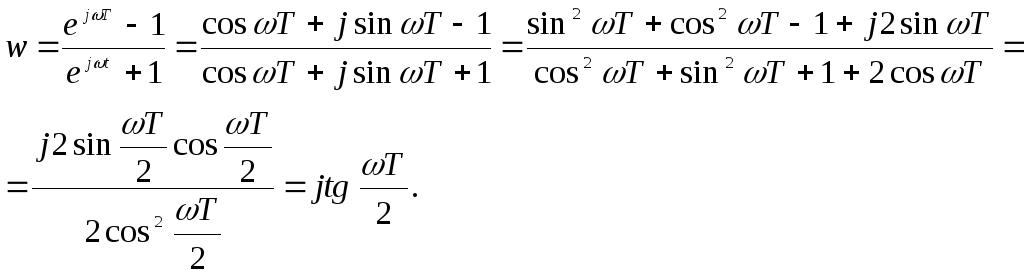
Правая часть этого равенства – величина мнимая, поэтому и левая часть будет мнимой величиной. Вводя обозначение , получим

или (8)

Переменную называют псевдочастотой, так как это безразмерная величина. Реальная частота связана с псевдочастотой соотношением

(9)

Для исследования импульсных и цифровых систем в ряде случаев более удобна размерная псевдочастота , которая связана с псевдочастотой зависимостью

(10)

Тогда

(11)

Переменную  называют абсолютной псевдочастотой. Из выражения (10) следует, что при <<2 абсолютную псевдочастоту  в расчетах и при построении ЛЧХ можно заменять действительной частотой .

Соотношение (6) может быть представлено с учетом (11):

(12)

Поясним смысл преобразования (6). Использование подстановки при замене р на позволяет отобразить левую полуплоскость плоскости Р внутрь круга единичного радиуса плоскости Z. Функция является периодической функцией с периодом , поэтому для обхода всей окружности единичного радиуса достаточно изменять частоту в интервале или в интервале . При этом отрезок мнимой оси от до преобразуется в окружность единичного радиуса (рис.1, а, б). С помощью соотношения (6) возможно отображение всех точек Z-плоскости, расположенных внутри круга единичного радиуса, в соответствующие точки левой полуплоскости W. Подобные отображения получили название конформных отображений (рис.1, б, в).

При изменении частоты в интервале абсолютная псевдочастота принимает все значения, принадлежащие интервалу . На рис.2 представлен график значений псевдочастоты. Операция W-преобразования в виде

конформно отображает левую полуполосу - , Re q<0 плоскости q (иначе р) на левую полуплоскость плоскости W, причем мнимая положительная полуось плоскости W является образом отрезка мнимой положительной полуоси плоскости q длиной . Начало этого отрезка находится в начале координат.

Понятие псевдочастоты позволяет строить так называемые логарифмические псевдочастотные характеристики дискретных САУ.

p

z

W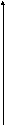

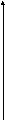
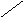Im Im

Im

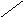
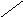
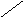
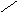
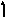
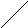
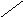
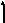
=+- /T 1  0

0

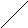
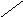Re =0 Re Re

-

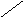а) б) в)

Рис.1

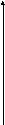
-3 -2 - 0 2 3

-

Рис.2