Министерство образования и науки Российской Федерации

ФГАОУ ВПО Уральский Федеральный Университет

имени первого Президента России Б.Н. Ельцина

кафедра теоретической теплотехники

анализ политропного процесса смеси идеальных газов

курсовая работа по технической термодинамике

Вариант 4

Преподаватель Нейская

Студент Иванова И.Л.

Группа Т-200901

Екатеринбург

2011

Оглавление

1. Теоретический анализ обратимого политропного процесса………………………………………………………………………...3

   1. Определение политропного процесса…………………………………….…3

   2. Вывод уравнения политропного процесса в переменных………………....3

   3. Способы определения показателя политропы………………………….…5

   4. Вычисление параметров состояния в начале и в конце процесса………6

   5. Вычисление теплоемкости и количества теплоты процесса……….….6

   6. Вычисление работы изменения объема и внешней работы………….…..6

   7. Вычисление изменения термодинамических функций……………….…..7

2. Расчет политропного процесса…………………………………...10

   1. Расчет термодинамических свойств……………………………………..10

      1. Расчет газовых постоянных и удельных массовых теплоемкостей.10

      2. Вычисление массовых долей компонентов смеси……………………....10

      3. Удельные теплоёмкости смеси…………………………………………….11

      4. Газовая постоянная смеси…………………………………………………..11

      5. Показатель адиабаты смеси……………………………………………….11

   2. Определение параметров в начале и в конце процесса…………………..11

   3. Расчет удельных характеристик процесса………………………………12

      1. Удельная работа изменения объема………………………………………12

      2. Удельная внешняя работа……………………………………………..……12

      3. Удельное количество теплоты процесса…………………………..……12

      4. Расчёт изменения термодинамических функций………………………12

      5. Проверка расчётов по первому закону термодинамики………………13

      6. Изображение процесса на диаграммах 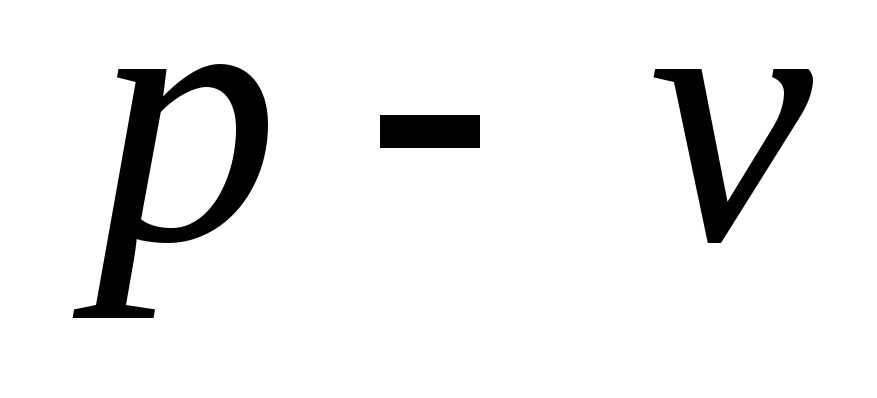и ……………….14

Основные обозначения……………………………………………………15

Список использованных источников……………………………..16

1. Теоретический анализ обратимого политропного процесса.

1.1. Определение политропного процесса

По определению политропным процессом называется процесс с постоянной заданной теплоёмкостью c_n или, что то же, с постоянным заданным отношением работы процесса к теплоте процесса на любой стадии его протекания, т.е.

Анализ процесса включает

1. вывод уравнения политропного процесса в переменных;

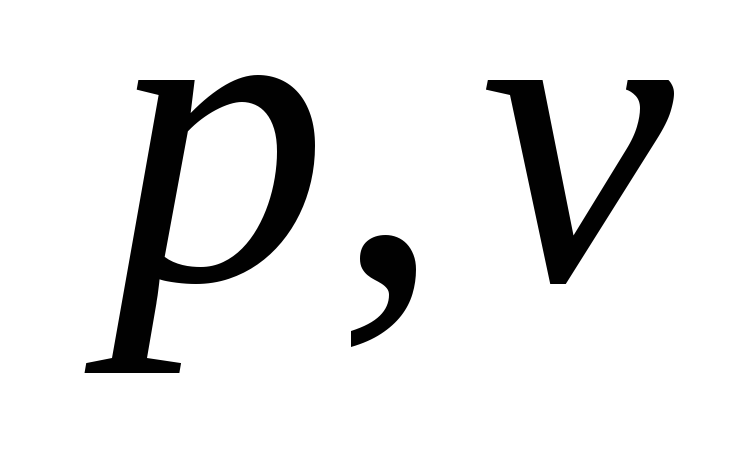2. вычисление параметров состояния в начале и в конце процесса;

3. вычисление теплоемкости c_n и количества теплоты процесса q;

4. вычисление работы изменения объема l и внешней работы процесса l`.

5. вычисление изменения термодинамических функций:

a) внутренней энергии ,

b) энтальпии ,

c) энтропии .

6) изображение процесса на диаграммах и .

Рабочее тело – идеальный газ, подчиняющийся уравнению состояния

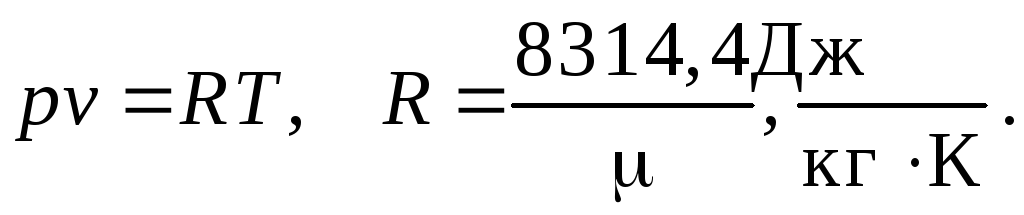
Анализ проводится для 1 кг рабочего тела при постоянных теплоёмкостях , вычисляемых с помощью молекулярно–кинетической теории.

1.2. Вывод уравнения политропного процесса в переменных (p,v)

Выражения первого начала термодинамики можно записать в двух эквивалентных формах (через внутреннюю энергию и через энтальпию):

Здесь

(два последние равенства представляют собой закон Джоуля: внутренняя энергия и энтальпия идеального газа не зависят только от температуры).

Подставив в уравнения и исключая из них , после простых преобразований получим

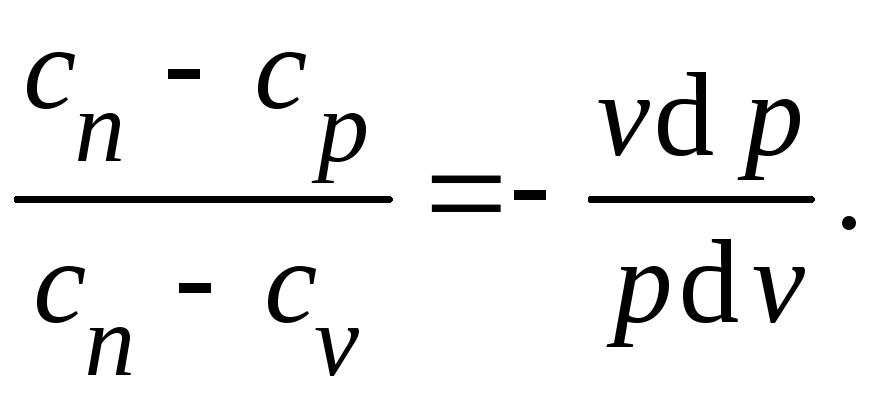
Постоянная величина

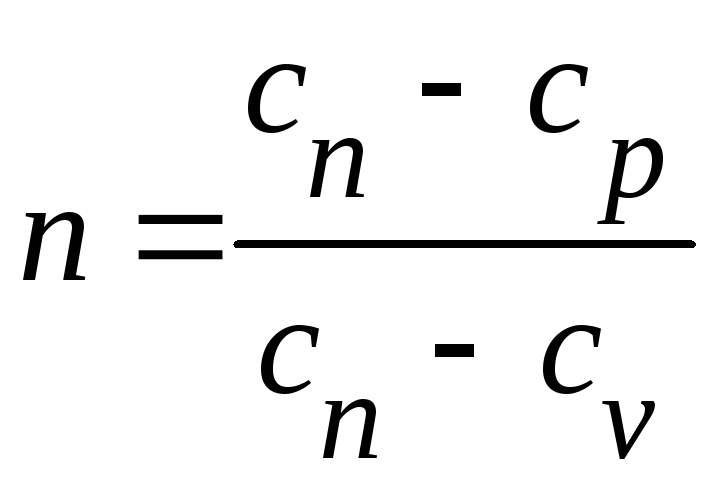
Называется показателем политропы.

Выражение записывается в виде дифференциального уравнения первого порядка с разделёнными переменными

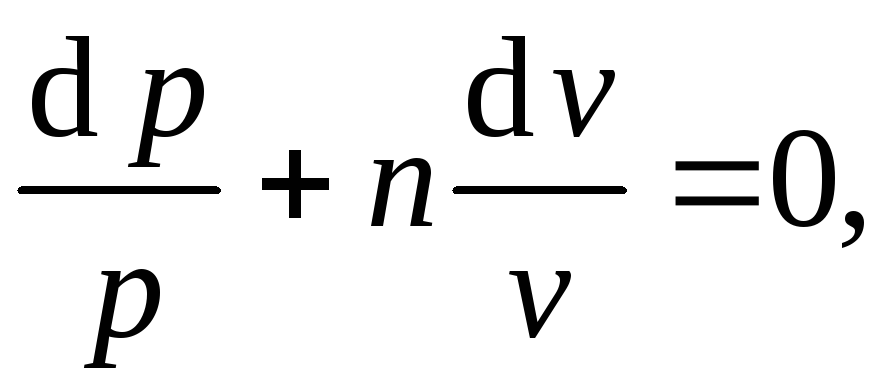
решение которого имеет вид:

Или

(8)

Графическое изображение политропного процесса.

Зависимость для различных значений показателя политропы представлена на рис.1.

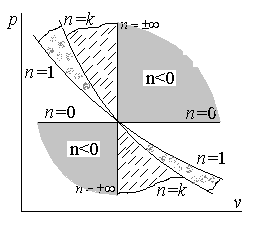
Рис.1. Изображение политропного процесса в диаграмме для различных значений показателя политропы .

1.3. Способы определения показателя политропы

Выражение (4) для показателя политропы n представляет собой отношение внешней работы и работы расширения, которые на диаграмме p – v графически изображаются площадями слева от кривой процесса и под ней соответственно (рис. 2).

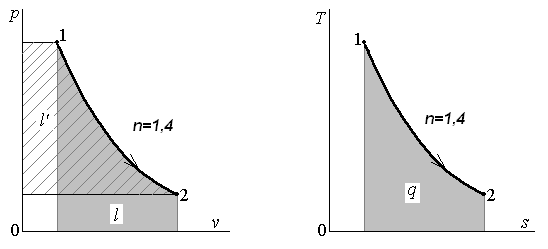
Рис. 2. Графическое определение показателя политропы

(9)

Таким образом, для определения показателя политропы необходимо знать, что процесс является политропным, и иметь его изображение на диаграмме p – v. Такой способ называется графическим.

Показатель политропы можно определить также по значениям двух параметров в начале и в конце процесса. Записывая уравнение политропного процесса, например, для известных давлений и объемов в начале и в конце процесса (точки 1 и 2)

(10)

получим

(11)

Такой способ определения показателя политропы называется аналитическим.

1.4. Вычисление параметров состояния в начале и в конце процесса

Соотношение для давлений и объемов в начальном и конечном состояниях следует из (10); соотношения для температур и давлений или температур и объемов можно получить, выражая объемы и давления через температуры из уравнения состояния (1):

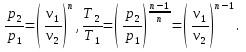(12)

1.5. Вычисление теплоемкости и количества теплоты процесса

При заданном значении показателя политропы из определения находим теплоёмкость политропного процесса:

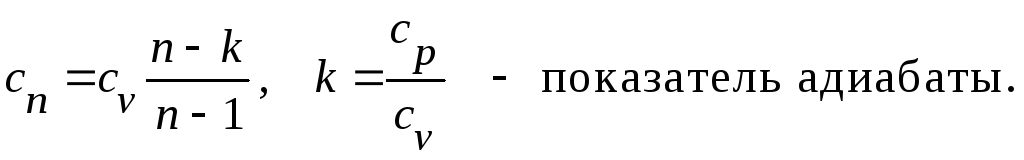(13)

Тогда теплота процесса ввиду постоянства теплоёмкости определится простым выражением:

(14)

1.6. Вычисление работы изменения объема и внешней работы

Работа изменения объема по определению

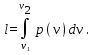
Поскольку теперь известно уравнение процесса в переменных p,v,

этот интеграл может быть вычислен:

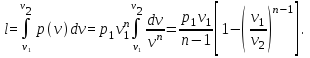(15)

Используя соотношение между давлением и объемом в политропном процессе и уравнение состояния, выражение для работы можно также записать в виде:

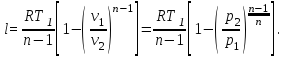(16)

Внешняя работа процесса.

Внешнюю работу процесса также можно вычислить, используя определение внешней работы и взяв соответствующий интеграл

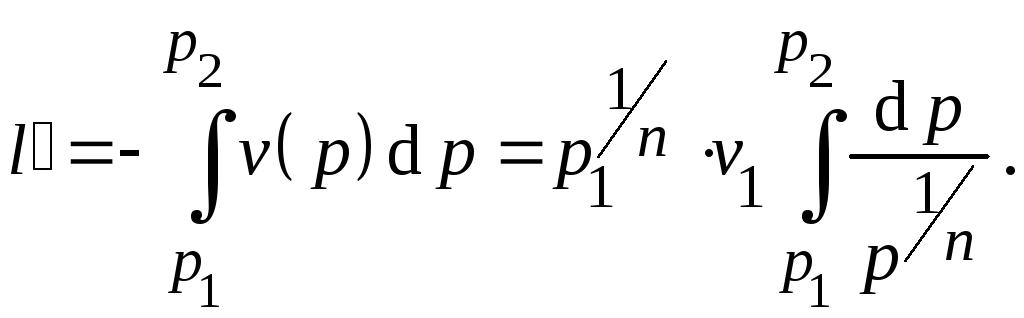
Однако проще получить это выражение, воспользовавшись определением показателя политропы (9), из которого видно, что внешняя работы в n раз больше работы изменения объема:

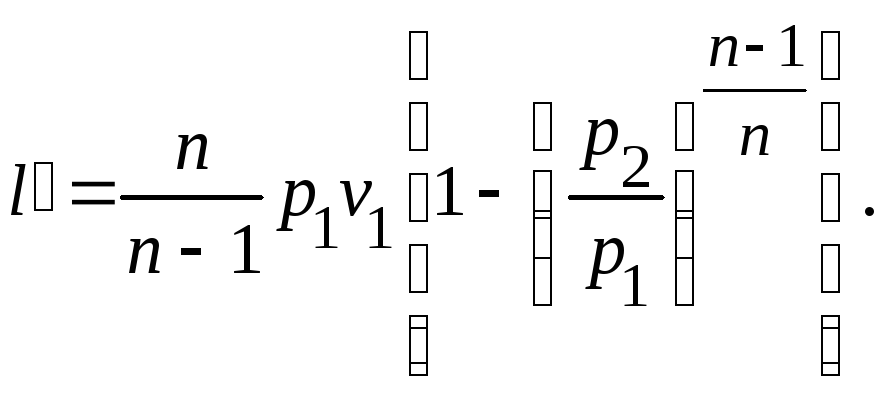(17)

1.7. Вычисление изменения термодинамических функций

Для вычисления изменения внутренней энергии и энтальпии необходимо проинтегрировать два последних уравнения в (3). Тогда

изменение внутренней энергии

(18)

изменение энтальпии

(19)

Выражение для изменения энтропии можно получить на основании II закона термодинамики для необратимых процессов:

(20)

Тогда изменение энтропии

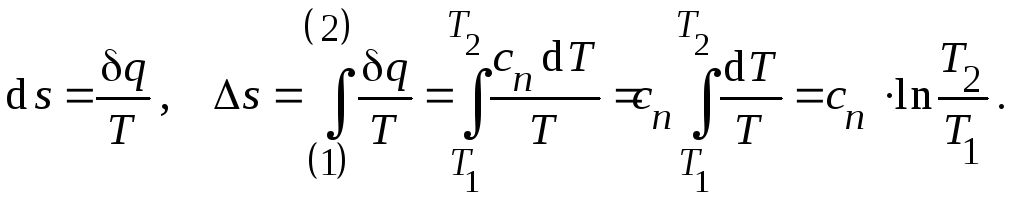(21)

Уравнение политропного процесса в переменных следует из определения количества теплоты через теплоёмкость (3) и из математической записи второго начала термодинамики (20):

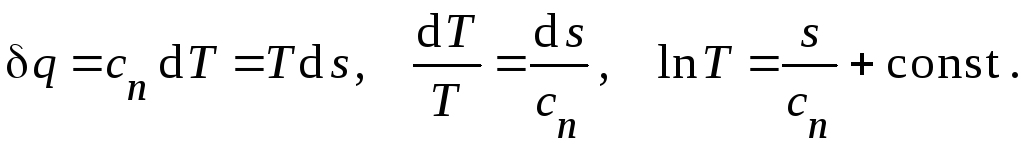
Если известны значения температуры и энтропии в начальном состоянии, то после нахождения произвольной постоянной получаем:

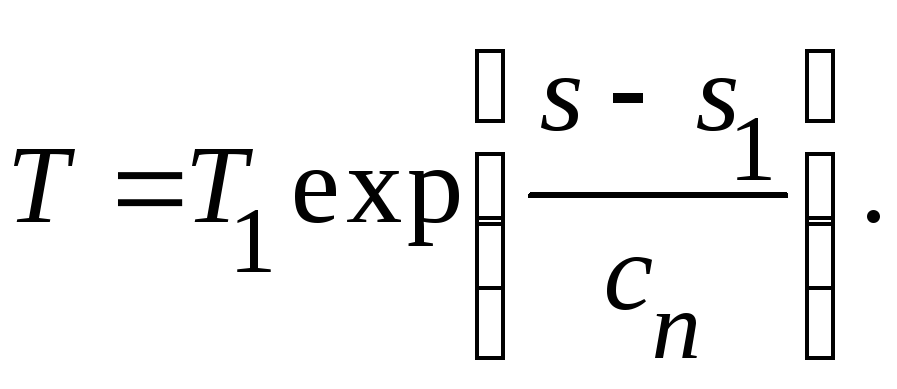(22)

Графическое изображение политропного процесса в переменных на основании (22) представлена на рис.3.

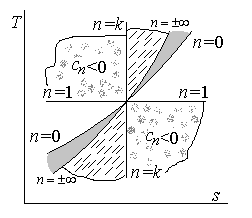
Рис.3. Изображение политропного процесса в диаграмме для различных значений показателя политропы .

Примечание. Для адиабатического процесса Расчёт проводится по приведённым формулам политропного процесса с заменой n на k. Из первого закона термодинамики при следует:

(23)

где вычисляются по формулам (18) и (19).

Проверка расчётов проводится на основе первого закона термодинамики:

(24)