Комбинированное управление.
Высокую
динамическую точность в тяжелых условиях
работы
следящих систем (при высоких скоростях
и ускорениях угла поворота входного
вала, при резких и значительных изменениях
момента
нагрузки на выходном валу и т. п.)
обеспечивают системы
с комбинированным управлением. Подобные
системы позволяют
выполнить так называемые условия
инвариантности. Система
автоматического управления является
инвариантной по
отношению к управляющему воздействию,
если после завершения
переходного процесса, определяемого
начальными условиями,
ошибка системы не зависит от этого
воздействия. Аналогично
формулируются условия инвариантности
по отношению к
возмущающему воздействию [3, 4].
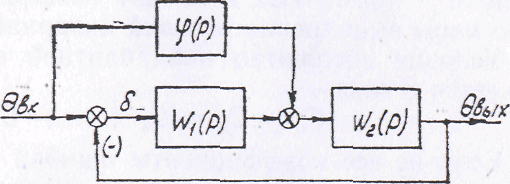
Рис.16
Для
структурной схемы следящей системы,
представленной на
риc.16,
задача инвариантности может быть
сформулирована следующим
образом: необходимо найти условия, при
которых выходная
величина Θвых
будет копировать без искажения и
запаздывания во времени входную
величину Θвх, т. е. необходимо, чтобы
передаточная функция замкнутой системы
была равна
 (33)
(33)
Для
следящей системы условие инвариантности
(33) эквивалентно
требованию
 (34)
(34)
где δ(p)
= Θвх
(p)
- Θвых(p)
– ошибка
системы.
Эквивалентная
передаточная функция замкнутой системы
может
быть получена на основе решения системы
уравнений
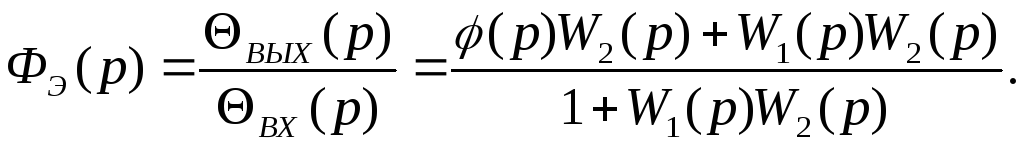 (35)
(35)
Для
обеспечения абсолютной инвариантности
в соответствии с
(31)
необходимо, чтобы

(36)
Применительно
к следящим системам для расчета
параметров
оператора φ(р) используют выражения для
коэффициентов ошибки
и применяют величину коэффициентов
ошибки в качестве
меры выполнения условий инвариантности.
Условие абсолютно инвариантной
следящей системы записывается
в виде
С0
= С1
=
С2
... = Ст
= 0.
Если не
все коэффициенты ошибки равны нулю, то
достигается
не абсолютная, а частичная инвариантность.
16


