Смещение в области оригиналов
Рассмотрим функцию
.
Если эта функция должна быть оригиналом,
то
- оригинал. При
это
условие очевидно выполняется, но при
значение функции
сказывается отличным от нуля при
.
Условимся, что смещенная дискретная
функция принадлежит функции
,
которые равны нулю, когда
.
При этом значение k будем
считать, когда выполняется условие:
,
при
(1)
Тогда справедлива Теорема 2:
Если
- оригинал и
-
ее изображение, то D-преобразование
смещенной решетчатой функции определяется
следующими уравнениями:
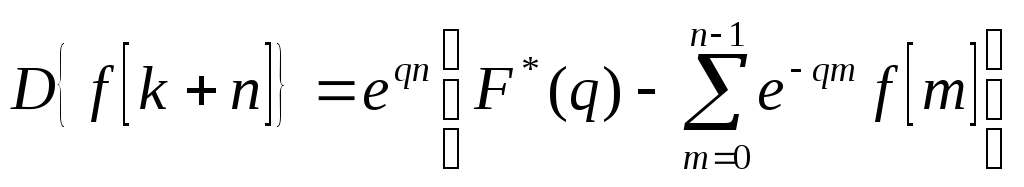при
(2)
при
(3)
Доказательство:
Воспользуемся формулой:
Предположим, что
и тогда получаем:
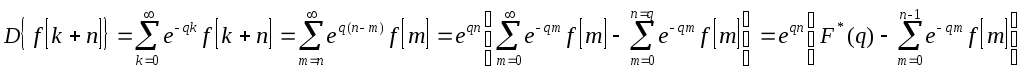Первое
слагаемое по условию теоремы есть
изображение
,
не создает остаток, это и есть равенство
(2).
При
:
В частном случае, когда функции
равны нулю. Тогда формулы (2) и (3) совпадают:
(4)