Динамические характеристики элементов сау.

Выше мы получили выражение (2.4), определяющее передаточную функцию линейного элемента системы управления. Это чрезвычайно важное выражение в теории автоматического управления. Оно связывает изображение выходного сигнала Y(s) c изображением входного сигнала Х(s) через динамические свойства элемента системы управления.

Ясно, что входное воздействие может иметь произвольный вид. Однако, чтобы охарактеризовать наиболее существенные черты динамического поведения объекта управления можно использовать некоторые "стандартные" виды входных воздействий. При этом выходной сигнал будет содержать определенную информацию о свойствах объекта управления.

Такие "стандартные" виды воздействий называются типовыми входными воздействиями. К ним относятся:

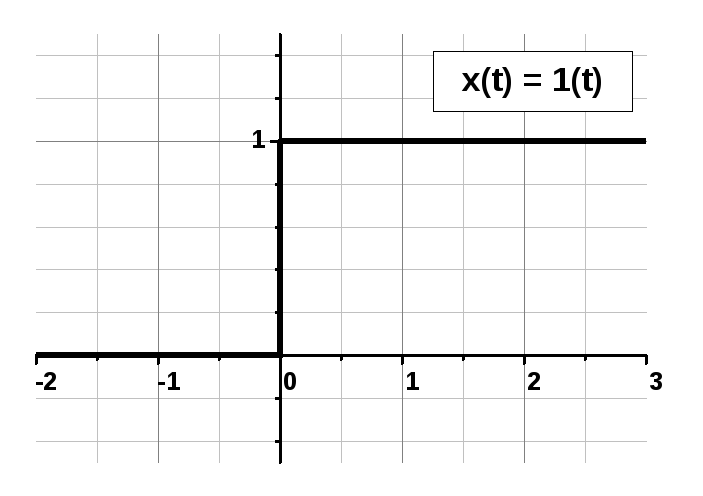
1. Единичная ступенчатая функция: 1(t).

2. Единичная импульсная функция: δ(t).

3. Гармонические функции: sin(ωt) и cos(ωt).

а) б)

Рис. 2.4. Единичная ступенчатая функция а) и единичная импульсная функция б).

Математически эти функции описываются следующим образом:

; .

Рис. 2.5. Гармонические функции.

Динамической характеристикой любого элемента системы управления называется его реакция на типовое входное воздействие. В зависимости от вида типового воздействия разделяют временные и частотные характеристики.

Временные характеристики:

• переходная характеристика h(t);

• весовая функция или импульсная переходная функция w(t).

Частотные характеристики:

• амплитудно-фазовая частотная характеристика (АФЧХ) или частотная передаточная функция;

• амплитудная частотная характеристика (АЧХ);

• фазовая частотная характеристика (ФЧХ);

• логарифмическая амплитудная частотная характеристика (ЛАЧХ либо ЛАХ);

• логарифмическая фазовая частотная характеристика (ЛФЧХ либо ЛФХ).

Перечисленные выше характеристики могут быть сняты экспериментально или построены по уравнению звена. Имеется и обратная возможность – по экспериментально полученным характеристикам составить уравнение звена. Кроме того, с помощью этих характеристик можно определить реакцию звена на любое возмущение произвольного вида. Эти характеристики являются исчерпывающим описанием динамических свойств звена.

Переходные характеристики.

Переходная, или временная, характеристика (функция) звена представляет собой реакцию на выходе звена, вызванную подачей на его вход единичного ступенчатого воздействия. Единичное ступенчатое воздействие (единичная ступенчатая функция) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным. Сказанное иллюстрируется на рис.2.6,а и б. На рис. 2.6,б показаны три различных вида переходных характеристик, соответствующих различным типам звеньев, которые мы рассмотрим далее.

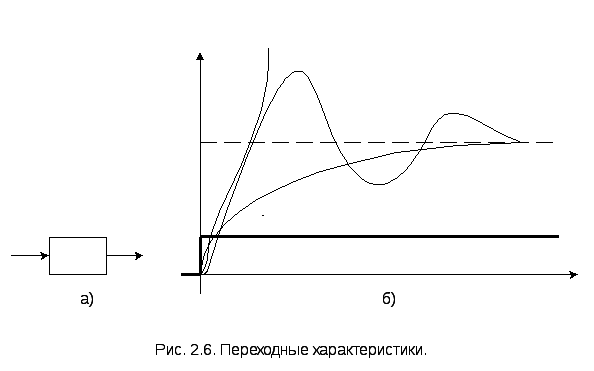
Таким образом, h(t) – это выражение для y(t) при x(t) = 1(t).

Наряду с переходной характеристикой применяется импульсная переходная (временная)характеристика или функция, называемая еще весовой функцией (функцией веса). Эта характеристика представляет собой реакцию звена на единичный импульс. Единичный импульс (единичная импульсная функция, или дельта-функция) – это математическая идеализация предельно короткого импульсного сигнала. Единичный импульс – это импульс, площадь которого равна единице при длительности, равной нулю, и высоте, равной бесконечности. На рис.2.4,б он условно показан в виде утолщения на оси ординат. На рис. 2.7 изображены типичные формы самих импульсных переходных характеристик.

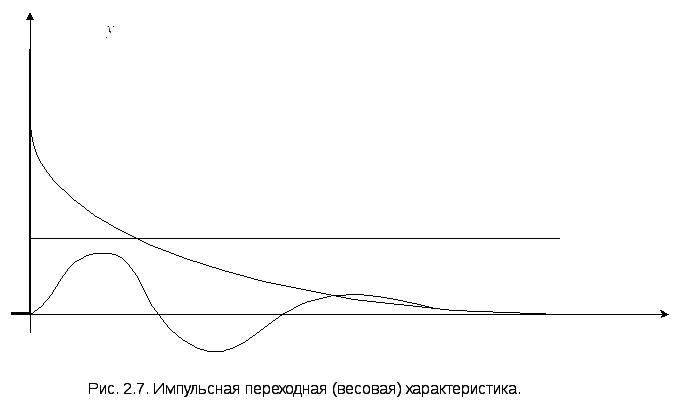
Импульсная переходная характеристика обозначается w(t); единичный импульс обозначается δ(t). Таким образом, w(t) – это y(t) при x(t) = δ(t).

При этом, согласно определению,

.

Дельта-функция просто связана с единичной ступенчатой функцией:

.

Из этого выражения следует аналогичная связь между переходной и весовой функциями линейных звеньев:

w(t) = h’(t)

и наоборот

.

Учитывая это простое соотношение между переходной и весовой функциями, ниже будем применять главным образом первую из них, имея в виду, что вторую при необходимости всегда можно получить дифференцированием по формуле w(t) = h’(t).

Зная переходную или весовую функцию, можно определить реакцию звена на произвольное входное воздействие при нулевых начальных условиях с помощью следующих формул:

, (2.8)

где х(0) – значение х(t) при t = 0;

. (2.9)

Эти формулы легко получаются друг из друга, являясь вариантами интеграла Дюамеля, или интеграла свертки.

Переходные характеристики могут быть выражены непосредственно через передаточную функцию звена с помощью преобразования Лапласа над уравнением звена, записанным в общем виде согласно уравнению (2.3,а):

.

Считая начальные условия нулевыми и учитывая, что обе части этого уравнения представляют собой сумму производных с постоянными коэффициентами, получим:

.

Здесь - изображения Лапласа функций x(t) и y(t); Q(s) и R(s) – полиномы, отличающиеся от исходных полиномов Q(p) и R(p) только заменой оператора дифференцирования р на комплексную переменную s = c + jω. Отсюда

, (2.10)

где - передаточная функция звена (с заменой р на s).

В случае, когда входное воздействие x(t) представляет собой единичный импульс δ(t), учитывая, что его изображение по Лапласу , из (2.10) получаем следующее выражение для изображения весовой функции звена:

, (2.11)

т.е.

.

Таким образом, весовая функция определяется через передаточную функцию по формуле обратного преобразования Лапласа, т.е. является ее оригиналом.

В случае, когда x(t) = 1(t), учитывая, что L[1(t)] = 1/s, из (2.10) получаем выражение для изображения переходной характеристики:

.

Соответственно переходная характеристика звена

.

Выражения (2.10) и (2.11) можно трактовать как определения передаточной функции. Согласно (2.10), передаточная функция определяется как отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях. Согласно (2.11), передаточная функция есть изображение Лапласа весовой функции.