лекции / Лекция1 / Лекция 9

Лекция № 9

МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

В технике существует класс объектов и процессов, управление которыми осуществляется на основе ограниченного числа решений, принимаемых последовательно в некоторые фиксированные моменты времени. Для решения задач оптимизации таких объектов американским ученым Р. Беллманом предложен метод, названный динамическим программированием.

В основу динамического программирования положен принцип оптимальности. Согласно ему оптимальное управление определяется конечной целью управления и состоянием системы в рассматриваемый момент времени независимо от того, каким образом система пришла в это состояние, т. е. оптимальное управление не зависит от предыстории системы. Это значит, что для любой оптимальной траектории каждый участок, связывающий любую промежуточную точку этой траектории с конечной, также является оптимальной траекторией.

Задачей оптимизации считается определение оптимальных управлений u°(t) и траектории Х°(t) из условия минимума (максимума) функционала

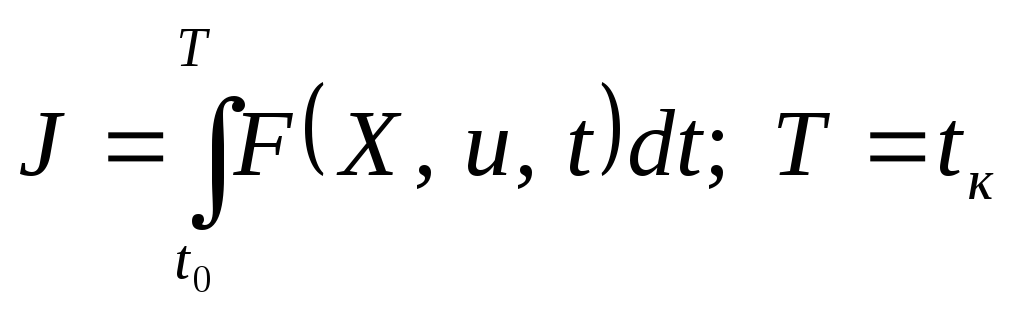(3.91)

для заданных уравнений состояния объекта

, (3.92)

а также начальных и конечных фиксированных значений X(t₀) и Х(Т) и интервала t₀  t  Т при наличии ограничений вида X(t)  _x и u(t)  _u. Здесь _x и  _u – заданные допустимые области для координат состояния и управлений.

При этом вводится вспомогательная функция Беллмана

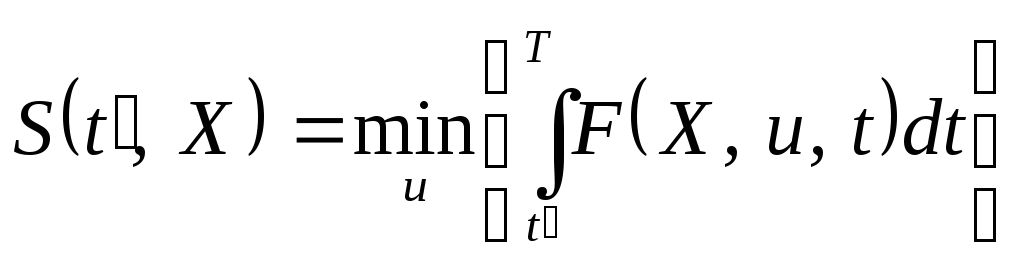. (3.93)

Минимум функционала (3.91) при условиях (3.92) зависит от момента времени , значения Х_t и конечного момента времени Т:

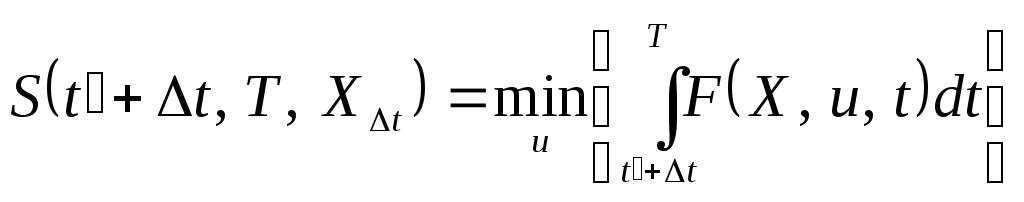, (3.94)

где – произвольный промежуточный момент времени в интервале – вектор коорди­нат состояния в момент времени .

Пусть – фиксированный момент времени, t – малое положительное число (). Тогда с учетом (3.94) вспомогательная функция

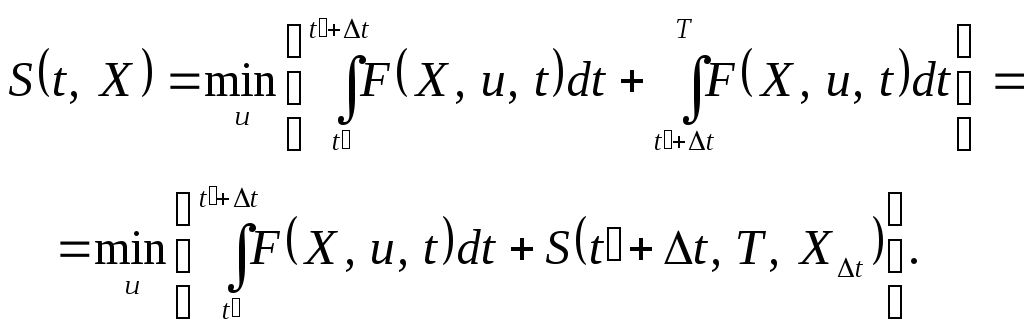(3.95)

Соответственно полученным из (3.95) величинам u°(t) по уравнениям (3.92) определяем оптимальные траектории вектора выхода Х°(t). При решении задач оптимизации объектов методом динамического программирования используют функциональные уравнения Беллмана в частных производных либо численные методы.

Уравнение Беллмана и его применение для синтеза оптимальных систем. Первое слагаемое в правой части выражения (3.95) с точностью до малых величин более высокого порядка, чем t, можно заменить приближенным значением

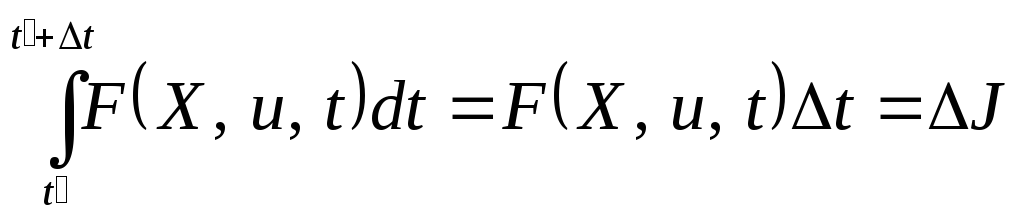. (3.96)

Второе слагаемое в правой части выражения (3.95), определяющее значение функции для любого момента времени , разложим в ряд Тейлора. Ограничиваясь линейными членами относительно приращений x_i и t и переходя к пределу, заменим это слагаемое приближенным значением, если функция S(t, X) имеет непрерывные частные производные по всем t и x_i(t):

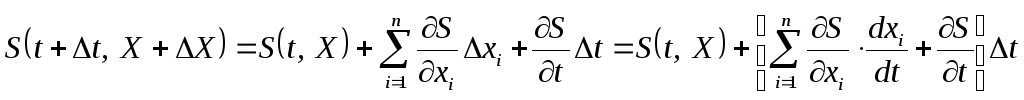. (3.97)

На основании (3.95), (3.96) и (3.97) запишем

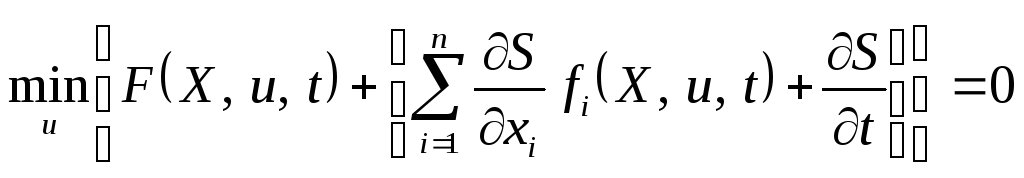(3.97)

при условиях

; (3.99)

.

Оптимальное управление u°(t) найдем в результате решения уравнения (3.98). Если координата управления ограничена u(t)  _u, то для внутренней точки области, определяемой множеством _u, условие (3.98) можно заменить функциональными уравнениям и в частных производных:

(3.100)

Если S не зависит явно от времени, то . В этом случае при решении уравнений (3.100) для квадратичных функций F(...) функционала (3.91) и t₀=0; t_к=T=. А.М.Лётовым [7] предложено искать вспомогательную функцию в виде квадратичной формы, дифференцируемой по всем координатам x_i:

. (3.101)

Для линейных объектов функция S(X) является функцией Ляпунова при t  . В результате решения (3.100) с учетом (3.101) найдем оптимальное управление в функции координат вектора состояния u°(X), которое обеспечивает устойчивые процессы.