Работа №2. «Анализ вероятностных сетевых графиков»

• Цель работы:

• Определить математическое ожидание времени выполнения каждой работы (операции) и дисперсию.

• Рассчитать параметры вероятностного сетевого графика и решить прямую и обратную задачу. В частности для прямой задачи принять директивный срок, округлив в большую сторону расчетный срок до значения кратного 5 или 10.

• Дано:

• Все данные из первой работы

• Переменные:

  • i – Номер начального события;

  • j – Номер конечного события;

  • t – Время выполнения данной операции (работы, задачи);

  • Tрн (i,j) – Раннее начало работы;

  • Tро (i,j) – Раннее окончание работы;

  • Tпн (i,j) – Позднее начало работы;

  • Tпо (i,j) – Позднее окончание работы;

  • R (i,j) – Полный резерв времени работы.

  • σ -дисперсия

  • z- аргумент функции Лапласа, нормального распределения

  • P(z)- значение вероятности

• Ход работы:

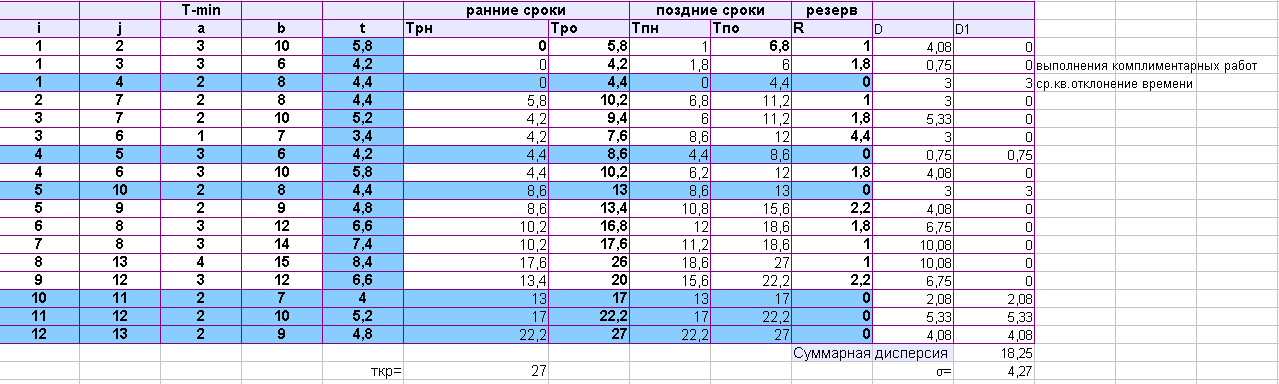
Прямая задача

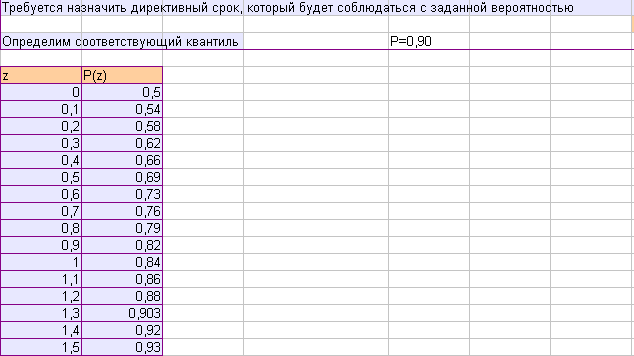
Обратная задача

• Описание алгоритма:

• Рассчитываем ранние и поздние сроки окончания работы аналогично первой работы. Определяем критические операции,​ у которых резерв времени равен 0.

• Находим сумму дисперсий для работ, лежащих на критическом пути и соответствующее среднеквадратическое отклонение.

• Решаем прямую задачу: определим вероятность соблюдения директивного срока, который назначали предварительно, путем округления в большую сторону до величины, кратной 5 дням.

• Квантиль нормального распределения z = Tdir-tкр/σ.

• Находим вероятность P(z) с помощью встроенной функции NORMSDIST из категории статистический.

• Обратная задача — назначение директивного срока проводим исходя из варианта P=0,90. Для этого, пользуясь функцией, NORMSDIST находим интервал, в котором лежит эта вероятность и, пользуясь линейной интерполяцией, определим соответствующий квантиль z. Tdir=tкр+σ*z

• Вывод:

Назначив директивный срок 33дня, мы выполним срок работ с вероятностью 90%

Работа №3. «Оптимизация сетевых графиков»

• Цель работы:

Найти жёсткость операции, затраты и ставку по кредиту.

Найти оптимальные варианты комплекса работ при различных ставках по кредиту.

• Дано:

• Все данные из первой работы

• Переменные:

• i – Номер начального события;

• j – Номер конечного события;

• t0 – Время выполнения данной операции в нормальном режиме;

• t1- Время выполнения данной операции в интенсивном режиме;

• с0 – затраты в нормальном режиме;

• c1 – затраты в интенсивном режиме

• Tрн (i,j) – Раннее начало работы;

• Tро (i,j) – Раннее окончание работы;

• Tпн (i,j) – Позднее начало работы;

• Tпо (i,j) – Позднее окончание работы;

• R (i,j) – Полный резерв времени работы

• A – Жесткость операции.

• a ,b,c – коэффициенты уравнения регрессии

• Y – затраты

• q –процентная ставка

• Ход работы:

Выполнила сжатие всех комплексов работ:

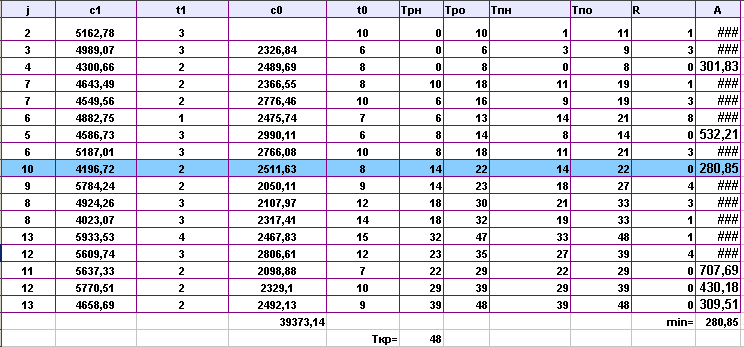
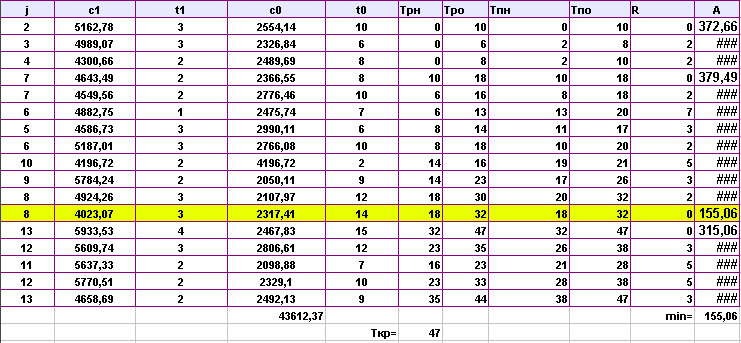
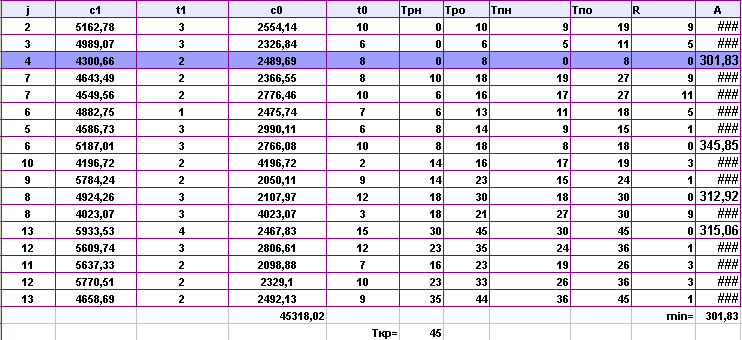
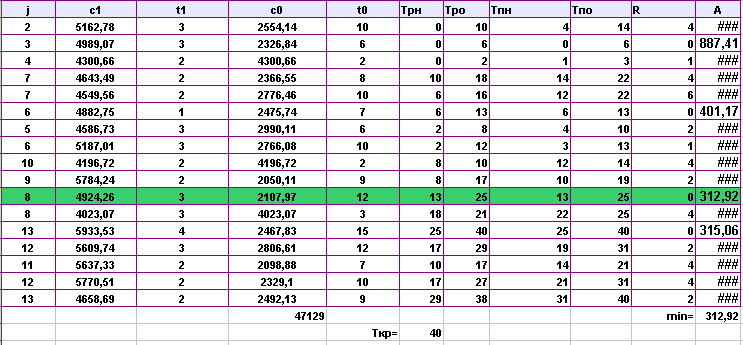
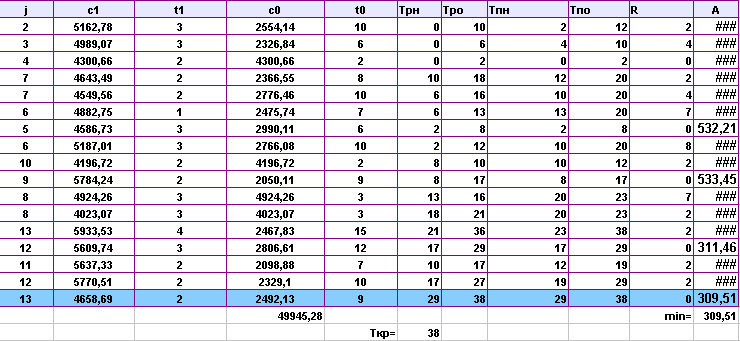
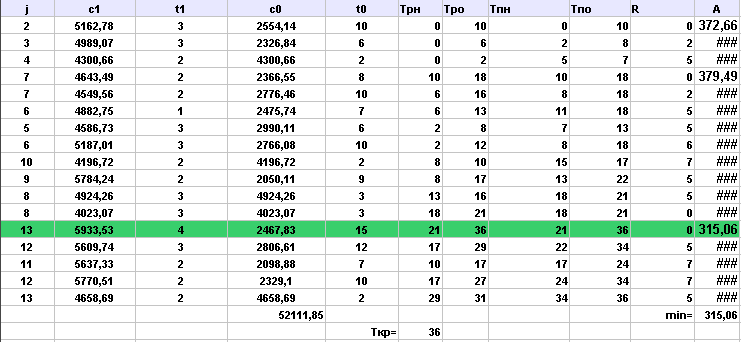
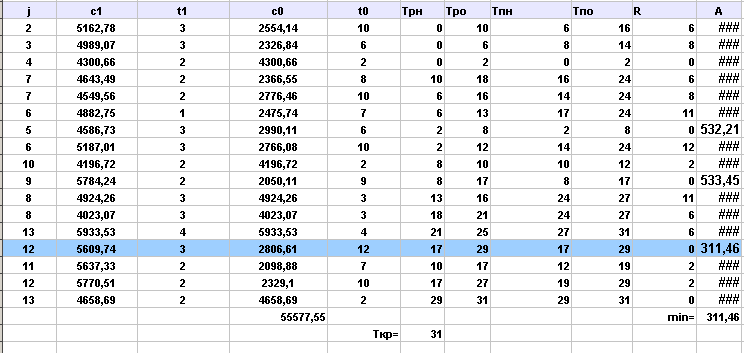
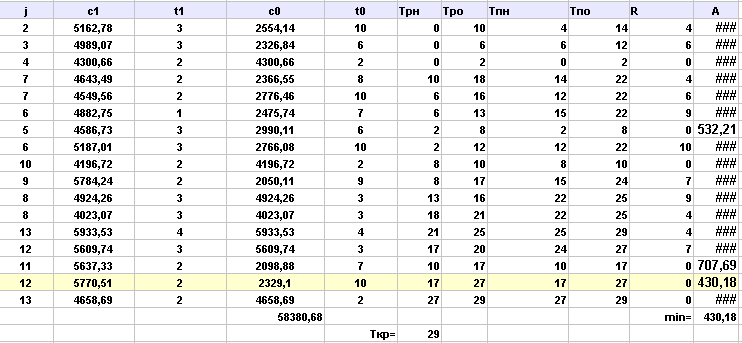
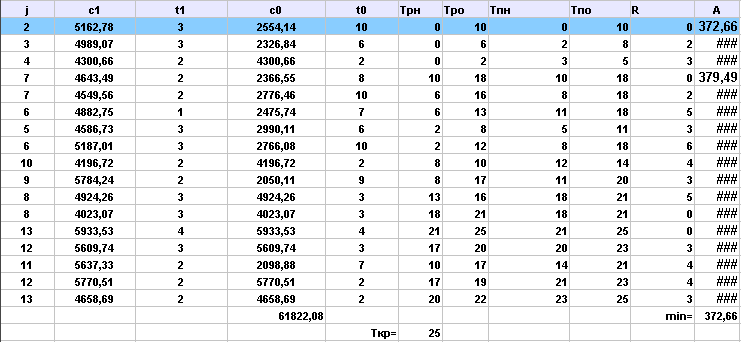
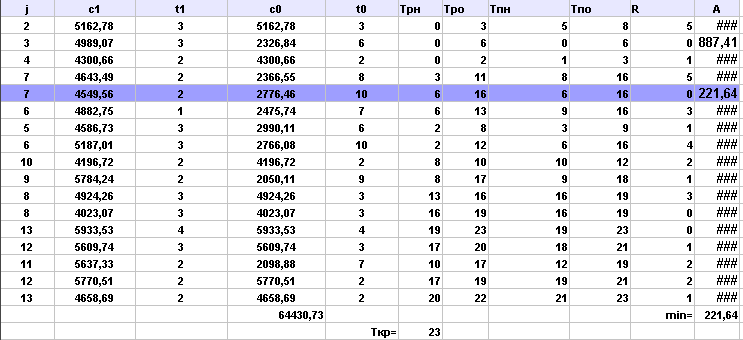
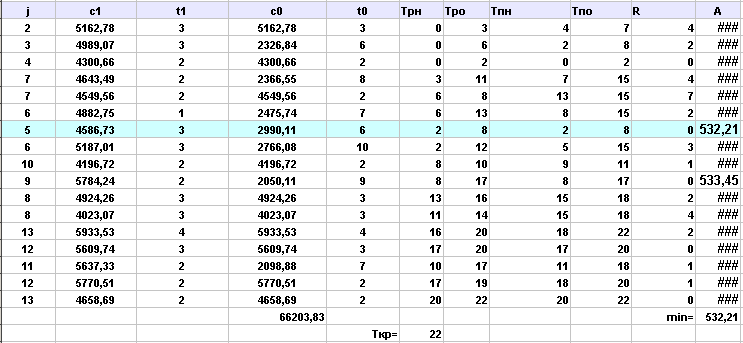
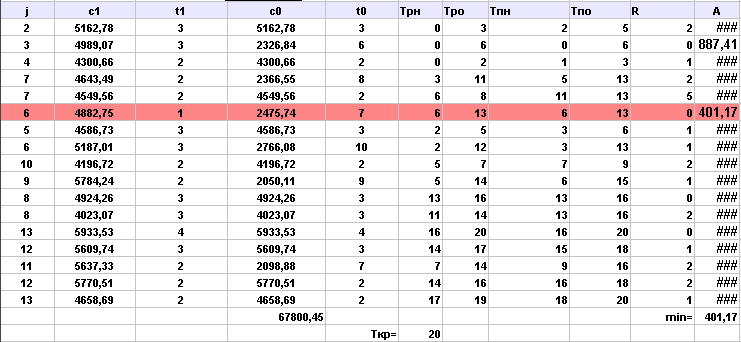
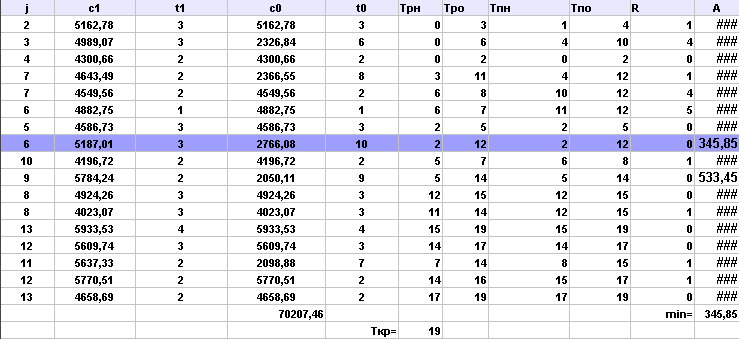
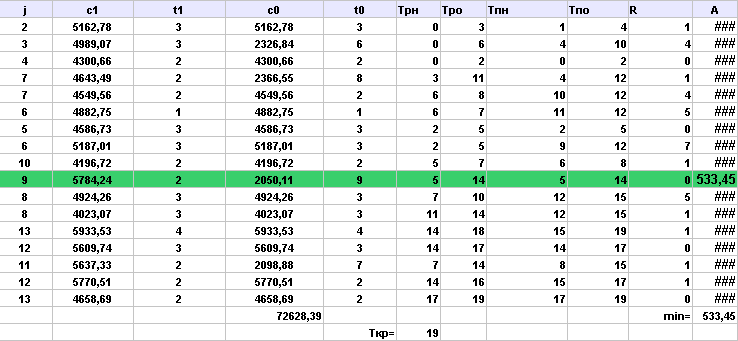
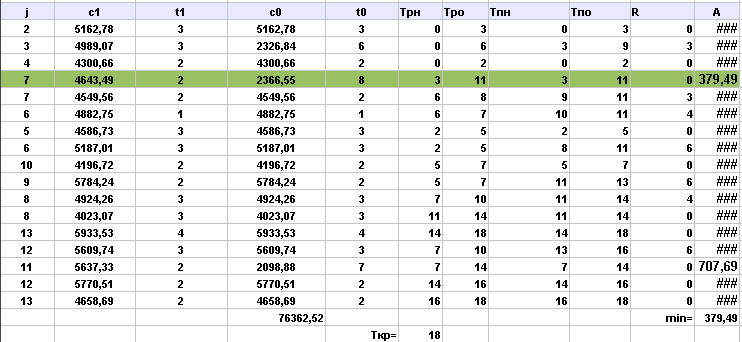
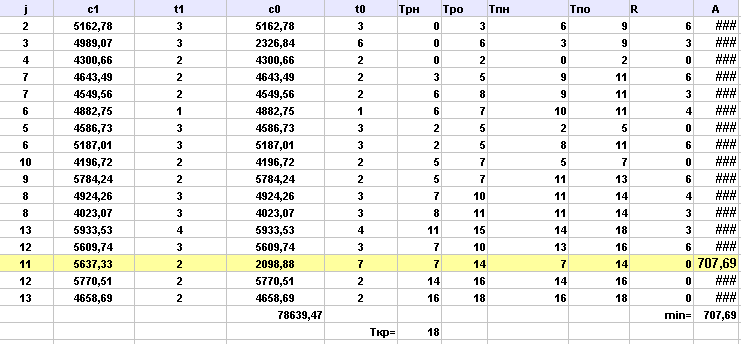
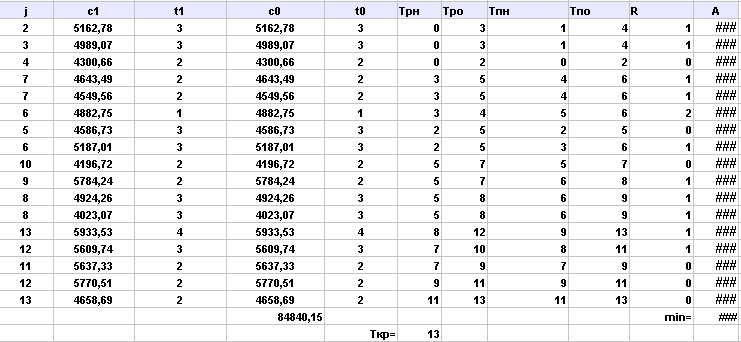
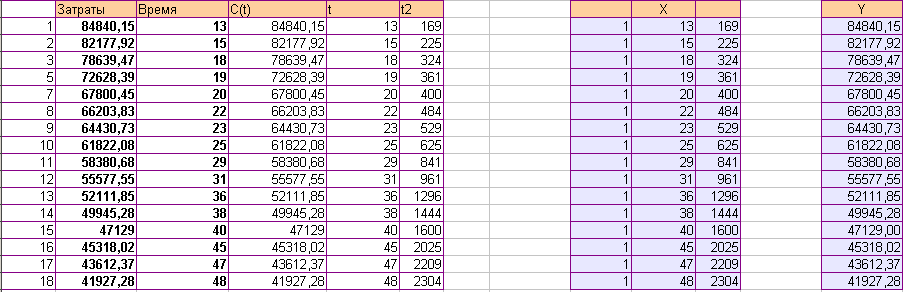
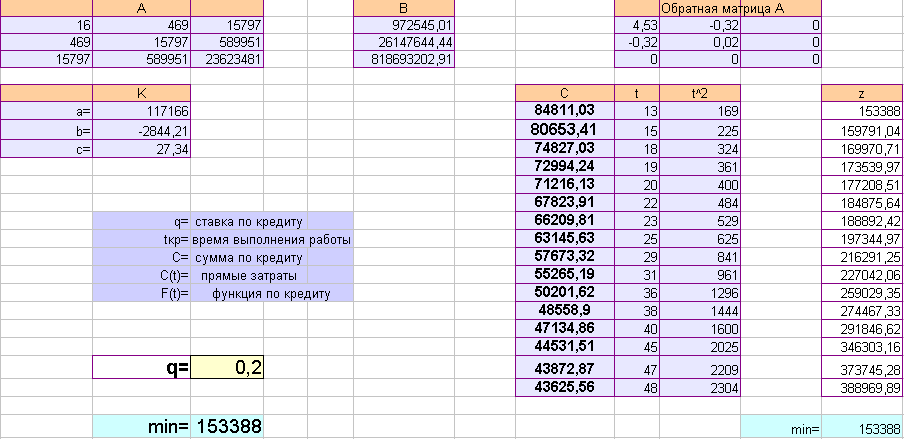
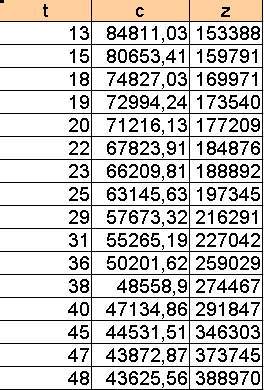
Аппроксимируем полученную статистическую зависимость (таблицу)

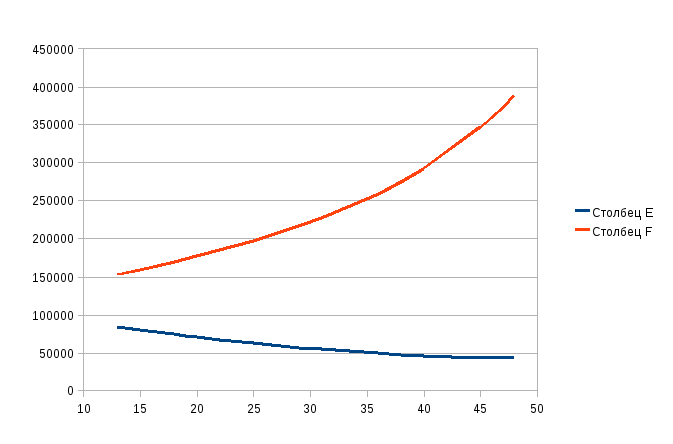
• Описание алгоритма:

• Для нормального режима работ находим резервы времени R

• Выделяем критический путь. Для всех операций, лежащих на критическом пути, находим жесткость по формуле A=(c1-c0)/(t0-t1).

• Проводим сжатие операций: из всех выбранных параметров А необходимо выбрать минимальное, пользуясь соответствующей функцией min. Таким образом, мы выявим операцию (работы, задачу), имеющую наименьшую жесткость и предназначенную для сжатия, которая заключается в повышении интенсивности (уменьшение времени с t0 до t1, увеличение затрат с c0 до с1)

• Для нахождения коэффициентов уравнения регрессии a,b,c используем метод наименьших квадратов.

• Создаем матрицу-столбец Y (значениями являются затраты), матрицу Х (матрица, в которой первый столбец содержит единицы, второй столбец содержит продолжительность выполнения комплекса работ, которым соответствует различная стоимость в массиве Y, третий столбец – тоже самое время в квадрате).

• С помощью встроенной функции MMULT из категории массив найдем A по формуле A=X^T *X. Для получения правой части системы уравнений используем формулу B=X^T *Y, пользуясь той же функцией MMULT. С помощью этой же функции находим коэффициенты уравнения: A*K=B; K=A^-1 *B.

• Обратная матрица находится с помощью функции MINVERSE.

• Чтобы учесть банковский процент, процентную ставку q задаем в отдельной ячейке, начиная с 0 с некоторым шагом, т.е. проводим расчет выплат по кредиту.

• Для каждой ставки q находим минимальное z, пользуясь функцией min, и соответствующее t.

• Полученные данные сводим в таблицу.

• Таким образом, мы располагаем информацией, при какой процентной ставке следует выполнить комплекс работ за время t и какие при этом будут выплаты по кредиту, которые являются минимальными для этой ставки.

• Вывод:

Теперь мы можем принят решение при какой процентной ставке следует выполнять комплекс работ за конкретное время и какие при этом будут выплаты по кредиту, которые являются минимальными для этой вставки