Метод д-разбиения

Замкнутой системе автоматического управления ставится в соответствие ее характеристическое уравнение .

.

Путем решения данного уравнения находятся корни и убеждаются, что из nкорнейm₁- правых,n- m₁ - левых.

Можно представить, что в гиперпространстве n+1-го порядкаn+1осей, по которым откладываются значения коэффициентов характеристического уравнения. Тогда каждому сочетанию этих конкретных параметров соответствует точка в гиперпространстве, а в плоскости корней характеристического уравнения в тоже время их конкретное расположение.

Если изменить один или несколько коэффициентов уравнения, точка в пространстве займет новое положение, корни в плоскости корней также сместятся. При непрерывном изменении коэффициентов корни будут выписывать годограф. И при каком-то сочетании коэффициентов уравнения один из корней попадет в начало координат, либо два корня на мнимую ось. Когда это случится, то уравнениепревратится в тождество:, потому как вещественная частьS в станет равна 0.

При дальнейшем изменении параметров может случиться, что еще какие-то корни "выедут" на мнимую ось. Этот случай также будет соответствовать уравнению .

Таким образом, условиепредставляет собой уравнение гиперповерхности в гиперпространстве, пересечение которой соответствует приобретению или потере характеристическим уравнением одного вещественного или двух комплексных правых корней.

На практике используется Д-разбиение по одному (не очень интересно), либо по двум параметрам.

Предположим, что нужно выяснить влияние на устойчивость системы двух параметров: и, которые входят в характеристическое уравнение замкнутой системы линейно. Тогда данное уравнение может быть приведено к виду

.

После замены в уравнении s на jполучается система уравнений:

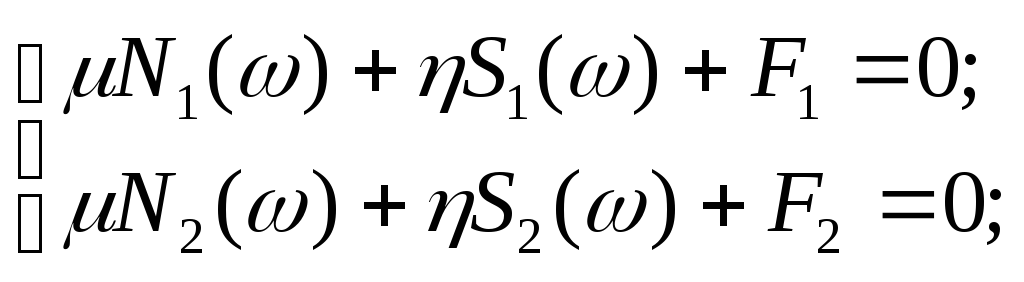так как,

решение которой, например, по правилу Крамера, позволяет получить  и как функции :

,,.

Следовательно можно построить однопараметрические зависимости ии отобразить их на плоскости параметров. Полученная кривая при изменении от до является кривой Д-разбиения плоскости где откладывается по оси абсцисс, а- ординат. При движении по кривой Д-разбиения в сторону возрастанияштриховку наносят слева, если определитель положителен. Точка по кривой пробегает дважды: первый раз при изменении  от до0, второй - при измененииот0 до. Однако при=0 определитель меняет знак, поэтому кривую оба раза штрихуют с одной стороны. Получается одна кривая с двойной штриховкой, соответствующая изменениюот0 до. При некотором значенииопределитель может обратиться в ноль. Если при этом соответствующие миноры не обращаются одновременно в ноль, то точка уходит в бесконечность. Если же одновременно с определителем обращаются в ноль и миноры, то рассматривается уравнение прямой линии

,

называемой особой прямой. Всем ее точкам соответствует одно и тоже значение .

Особые прямые получаются также из уравнения при и из уравненияпри , если в эти уравнения входит хотя бы один из параметровили .

Правила штриховки следующие:

• Если особая прямая и кривая Д-разбиения сближаются асимптотически - штриховка особой прямой однократная, направлена к заштрихованной стороне кривой Д-разбиения.

• если особая прямая имеет общую точку с кривой Д-разбиения, но не пересекает ее - штриховка особой прямой однократная и около общей точки направлена к заштрихованной стороне Д-разбиения.

• если особая прямая пересекает кривую Д-разбиения в двух точках - штриховка особой прямой двойная и направлена к заштрихованной стороне кривой Д-разбиения около той точки пересечения, в которой определитель меняет знак, около второй точки пересечения определитель знака не меняет и штриховку особой прямой не изменяют.

• если особая прямая пересекает кривую Д-разбиения, но знак определителя не меняется - особую прямую не штрихуют.

После того, как кривая Д-разбиения и особые прямые построены, и на них нанесена штриховка, отыскивается область, внутрь которой направлена штриховка ее границ. Это область потенциальной устойчивости. С помощью любого критерия устойчивости проверяется, является ли система в какой-либо точке данной области устойчивой. Тогда рассматриваемая область принимается в качестве области устойчивости. Возможны случаи, когда области устойчивости отсутствуют.

Методом Д-разбиения плоскости по двум параметрам иногда можно выяснить влияние на устойчивость одного параметра, который входит в характеристическое уравнение нелинейным образом.

Пример. Имеется система, передаточная функция которой

.

Требуется произвести D–разбиение поT₁ иК.Обозначим.

Характеристическое уравнение замкнутой системы

.

После преобразований

.

Для построения границы области устойчивости рассмотрим уравнение

,

которое, после разделения на мнимую и комплексную части, преобразуется в систему

; или .

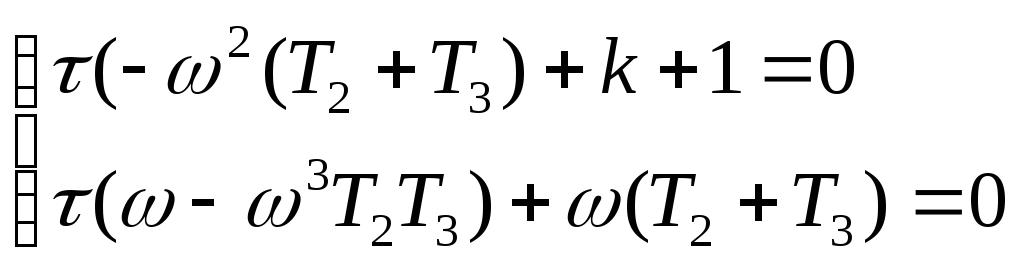Вычисляя соответствующие определитель и миноры

, ,

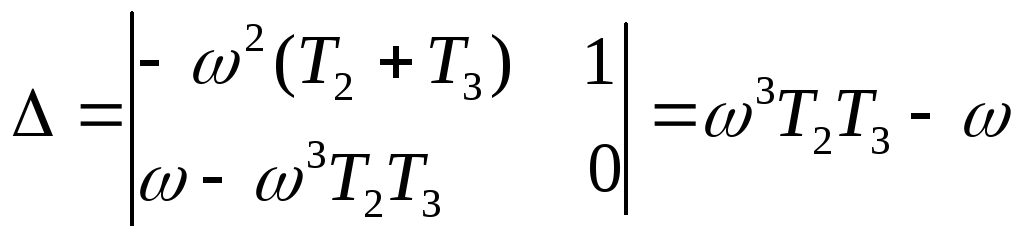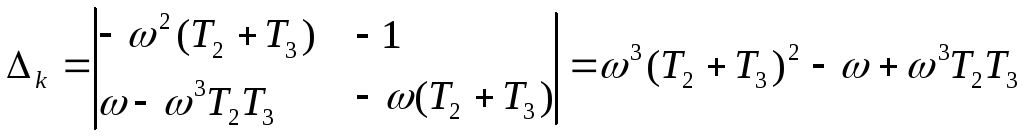, находим параметрические зависимости .

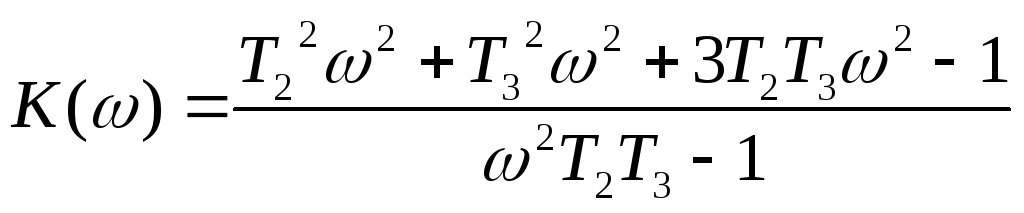В точке определитель обращается в ноль. Соответствующие кривые(),К() иК() терпят разрыв.

Особые прямые получаются из уравнений и, которые для данного примера имеют вид:К+1=0 иТ₂Т₃=0 соответственно.

Уравнения особых прямых:

К = -1; = 0.

Ниже на рисунке приведены зависимости (),К() и построена область устойчивости системы.

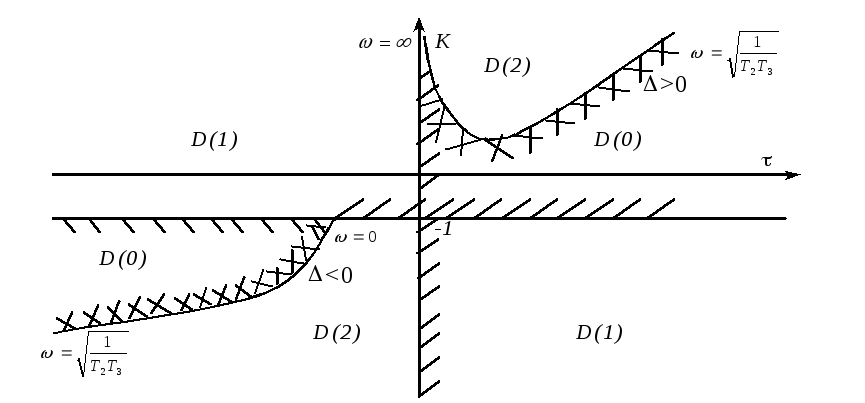Получили две области потенциальной устойчивостиD(0). Для проверки возьмем точку из верхней области (К=0, >0). Подставим эти значения в характеристическое уравнение: . В данной точке система будет устойчива, так все корни уравнения отрицательны. Аналогично проверяется и вторая область.

Область устойчивости, находящаяся в первом квадранте - рабочая область. Область устойчивости, находящаяся в третьем квадранте - область математически устойчивых решений (не рабочая).