3. Нахождение оригинала по известному изображению. Примеры

Рассмотрим простейшие приемы нахождения оригинала по известному изображению. Один из них основан на использовании таблицы изображений, которая в этом случае рассматривается в обратном порядке, и правил операционного исчисления. В первую очередь это относится к теореме смещения, интегрированию и дифференцированию изображения и изображению свертки функций.

Пример 12. Найти оригинал f(t), если .

Решение. Исходным можно взять соответствие

.

Операции смещения на а в области изображений соответствует операция домножения на в области оригиналов. Поэтому при а=1 имеем

.

Операции домножения на в области изображений соответствует запаздывание на =2 в области оригиналов. Следовательно,

Пример 13. Найти оригинал изображения .

Решение. Выделим в знаменателе полный квадрат

.

Воспользуемся равенством , а также теоремой смещения. В результате получим .

Пример 14. Найти оригинал, соответствующий изображению .

Решение. Можно поступить так: за исходное взять соотношение .

Затем воспользуемся тем, что делению на р в области изображений соответствует операция интегрирования в области оригиналов:

.

Это же свойство применим повторно:

.

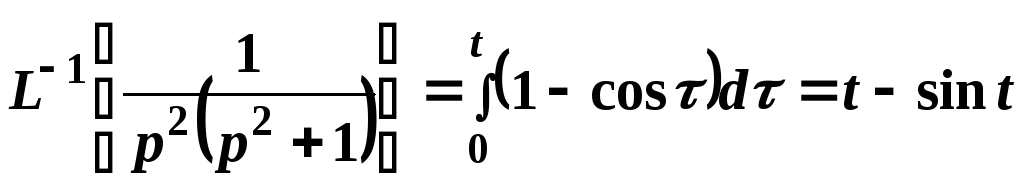Заметим, что оригинал указанного изображения проще можно было бы найти, если разложить его на простейшие дроби:

.

Согласно свойству линейности имеем

.

Пример 15. Найти оригинал изображения

.

Решение. Представим изображение в виде

.

Произведению изображений и соответствует свертка их оригиналов и . Поэтому

.

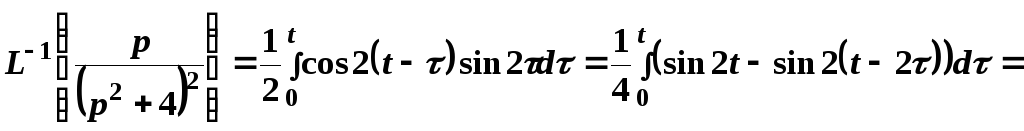
Для этого изображения оригинал можно найти проще, если воспользоваться тем, что операции дифференцирования в области изображений соответствует операция домножения на (-t) в области оригиналов. Поэтому

.

Очень часто при решении практических задач возникает необходимость нахождения оригиналов изображений, которые представляются в виде дробно рациональной функции

,

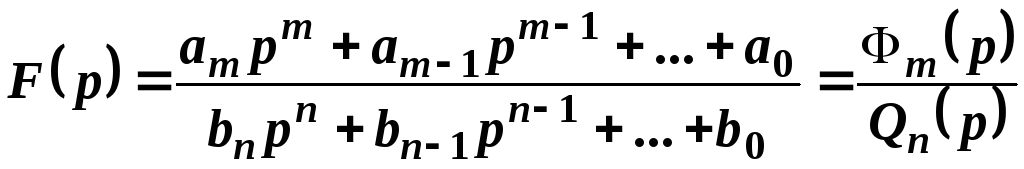в которой старшая степень числителя меньше старшей степени знаменателя переменной р.

При нахождении оригинала такой дроби разлагают ее на сумму простых дробей с помощью метода неопределенных коэффициентов, известного из интегрального исчисления. Затем находят оригиналы для каждой простой дроби.

Пример 16. Найти оригинал, соответствующий изображению

.

Решение. Разложим данную дробь на сумму простейших дробей. Для этого, прежде всего, найдем корни знаменателя, решив уравнение . Проверкой убеждаемся, что один из его корней. Разделим кубический многочлен на двучлен р+1. В частном получим . Дискриминант этого трехчлена - отрицательный, на действительные множители он не разлагается. Разложение данного изображения на простейшие дроби имеет вид:

.

Отсюда

.

Полагая в этом равенстве , находим . Затем приравниваем коэффициенты при одинаковых степенях р:

, .

Таким образом, .

В знаменателе второй дроби выделим полный квадрат, а в числителе - двучлен :

.

Используя свойство линейности , переходим в область оригиналов. Получим

.

Заметим, что в данном случае, прежде чем приступать к разложению изображения на простейшие дроби, было бы полезно воспользоваться теоремой смещения. Для этого в исходном изображении выделим двучлен :

.

Тогда

.

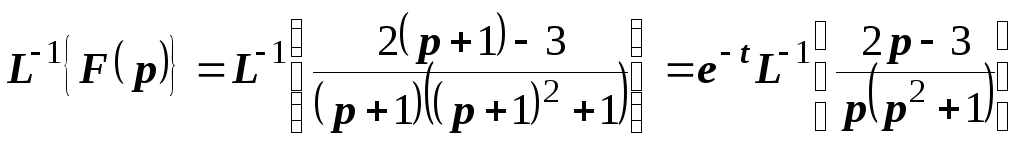Разложение полученного изображения на простейшие дроби проще, чем исходного:

; ; ; .

Оригиналом будет функция

или .

Задача нахождения оригиналов, соответствующих дробно-рациональным изображениям упрощается, если воспользоваться следующей краткой таблицей (табл. 3).

Таблица 3 – Изображение – оригинал

№	Изображение	Оригинал
1	2	3
1
2
3
4
5
6
7
8
9
1 11 0

Продолжение табл. 3

1	2	3
12
13
14
15
16
17
18
19
20
21