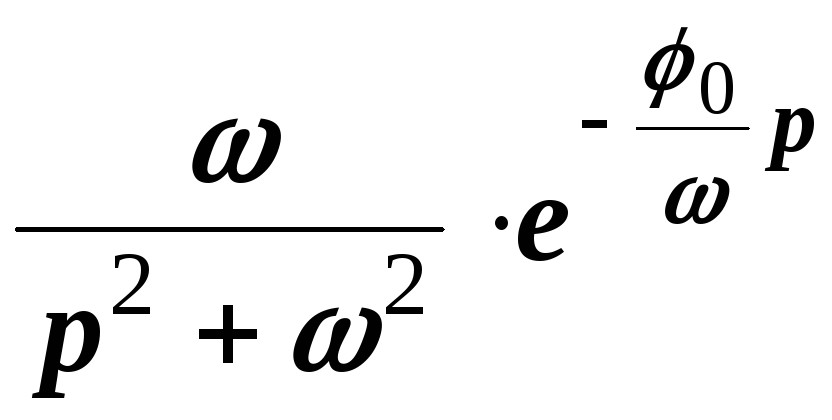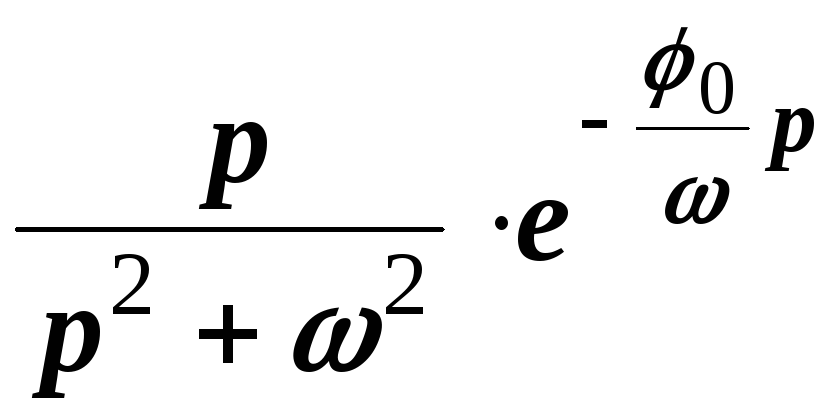2. Нахождение изображения функций. Примеры

Пример 1. Найти изображение единичной функции Хевисайда, которая обозначается и определяется в соответствии с равенством:

Решение. Пользуясь определением изображения по Лапласу, находим

.

Пример 2. Найти изображение функции

Решение. Имеем

.

Заметим, что указанную функцию можно записать короче, если использовать в качестве множителя единичную функцию (t), а именно:

.

Роль множителя (t) состоит в том, что он «гасит» (обращает в нуль) функцию при t < 0. В дальнейшем, говоря о функциях-оригиналах, будем считать, что все они снабжены множителем (t), хотя сам этот множитель в написании часто будем опускать. Так, например, мы будем писать tⁿ, e^at, sint и т. д., подразумевая при этом соответственно

и т. д.

Единичная функция играет важную роль в операционном исчислении. Зная ее изображение и используя правила операционного исчисления, можно найти изображения различных оригиналов. Например, используя теорему смещения, можно записать: из того, что , следует, что ,

и не пользоваться определением преобразования Лапласа, связанного с вычислением несобственного интеграла.

Пример 3. Найти изображения функций и .

Решение. Воспользуемся формулами Эйлера:

;

.

Согласно свойству линейности преобразования Лапласа имеем

.

Следовательно,

.

Точно также

,

то есть

.

Применяя к полученным соотношениям свойство смещения, находим

,

.

Точно также для гиперболических функций получаем соответствия:

;

.

Пример 4. Найти изображение функции tⁿ.

Решение. Используем теорему дифференцирования к изображению функции (t) . Получим

; .

.

Итак, .

Пример 5. Найти изображение функции

.

Решение. На основании формулы

заменим произведение на .

Тогда

.

Чтобы найти изображение исходной функции, воспользуемся тем, что операции умножения на в области оригиналов соответствует операция смещения на 3 в области изображений. Окончательно получим

.

Пример 6. Найти изображение функции

.

Решение. Воспользуемся соотношением

.

Далее, согласно правилу (8), операции деления на t в области оригиналов соответствует операция интегрирования в области изображений.

Поэтому

.

Итак,

.

Пример 7. Найти изображение функции

.

Решение. Предварительно найдем изображение функции , преобразовав ее по формуле . Имеем

.

Затем, используя тот факт, что операции интегрирования в области оригиналов соответствует операция деления на р в области изображений, окончательно получим

.

Пример 8. Найти изображение функции

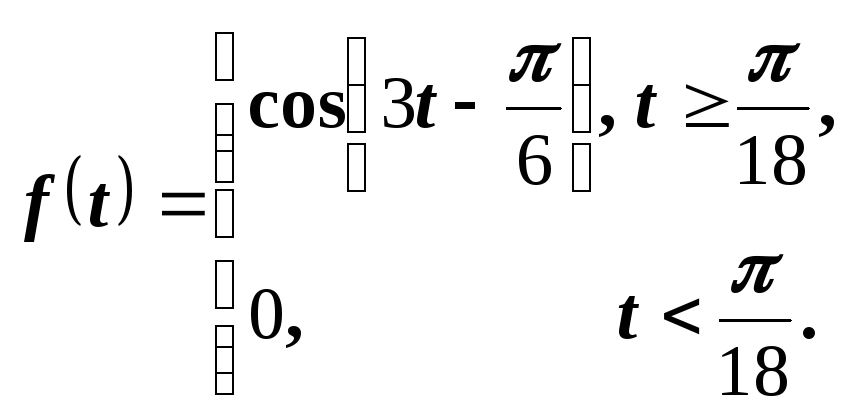
Решение. Воспользуемся равенством . Согласно теореме запаздывания имеем

.

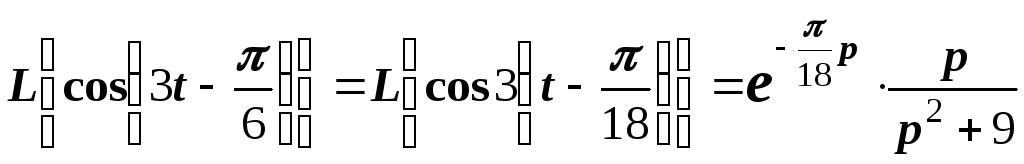В данном примере существенно равенство нулю функции при , т.е. возможность представления функции f(t) в виде

,

а соответственно, и возможность использования теоремы запаздывания.

Иначе поступаем, если функция задана следующим соотношением:

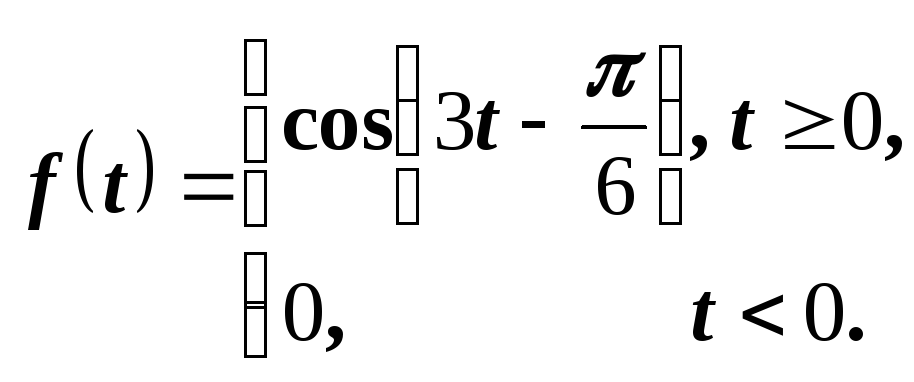
В этом случае осуществлен сдвиг вправо на графика функции , но не произведено «погашение» его нулем на участке . Поэтому запаздывания оригинала по времени не происходит, а функция представима в виде .

Для нахождения ее изображения воспользуемся равенством

.

Применив теоремы подобия и линейности, получим

.

Из этого примера следует, что при записи оригиналов, являющихся функциями запаздывающего аргумента , опускать множитель не рекомендуется во избежание недоразумений. Так, например, для обозначения оригиналов степенной и показательной функций запаздывающего аргумента с запаздыванием  следует пользоваться записью , , а не записью и .

Последнюю легко спутать с записью оригинала незапаздывающего аргумента: и .

Пример 9. Найти изображение функции

.

Решение. Для того, чтобы применить теорему запаздывания, предварительно преобразуем оригинал как функцию аргумента :

.

.

Заметим, что изображение этого оригинала можно найти согласно его определения:

.

Вычислив интеграл, мы получим тот же результат.

Теорема запаздывания является удобным способом для нахождения изображений кусочно-непрерывных функций.

Пример 10. Найти изображение функции

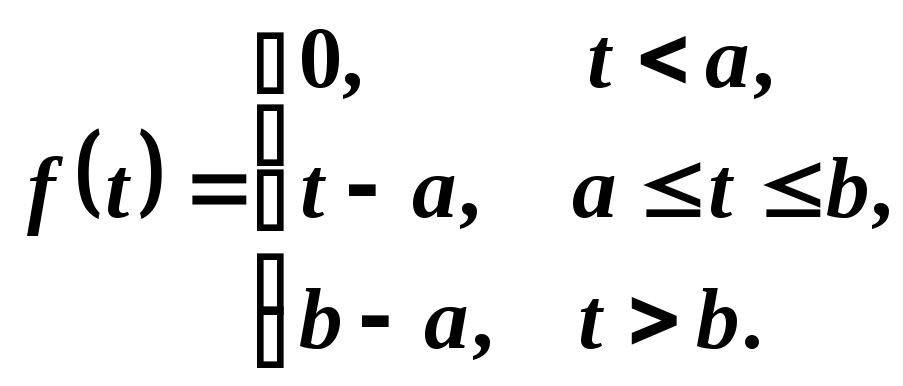
Решение. Пользуясь обобщенной единичной функцией, оригинал f(t) можно записать формулой

.

В этом равенстве отражен тот факт, что «сигнал» f₁(t)=(t-a) был "включен" в момент t=a и "выключен" в момент t=b. После этого включен сигнал f₂(t)=b-a.

Оригинал представим в виде

.

При нахождении его изображения исходим из соотношения

.

Используя теорему запаздывания оригинала, получим

Пример 11. Найти изображение функции

.

Решение. Функция есть свертка функций и . Согласно теореме умножения свертке двух функций соответствует произведение их изображений. Если учесть, что

, а ,

то указанной свертке оригиналов будет соответствовать изображение

.

Изображения элементарных функций получаются путем вычисления соответствующих несобственных интегралов, иногда довольно сложных и громоздких. Однако нет необходимости проделывать все вычисления каждый раз заново: достаточно составить таблицу изображений и пользоваться ею подобно тому, как мы пользуемся таблицей производных или неопределенных интегралов.

Приведем таблицу изображений наиболее часто встречающихся элементарных функций (табл. 2).

Таблица 2 – Оригинал – изображение

№	Оригинал	Изображение
1	1
2	t
3	tп
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18