2.4 Построение плана скоростей

Скорость точки А определяем по формуле

Вектор скорости направлен перпендикулярно звену в сторону, соответствующую направлению угловой скорости .

На плане скоростей скорость точки изображается отрезком .

Масштабный коэффициент плана скоростей

Скорость точки В определяем из системы уравнений

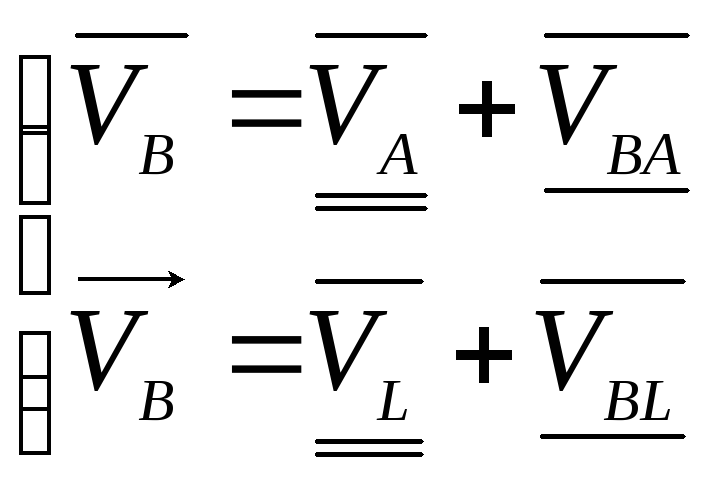
Решаем графически систему уравнений . Для этого из точки а проводим прямую, перпендикулярную к звену АВ, а с точки р_v, проводим прямую перпендикулярно звену ВL. В месте пересечения получаем точку b.

Скорости равны

Положение точек С и D определяем с соотношения

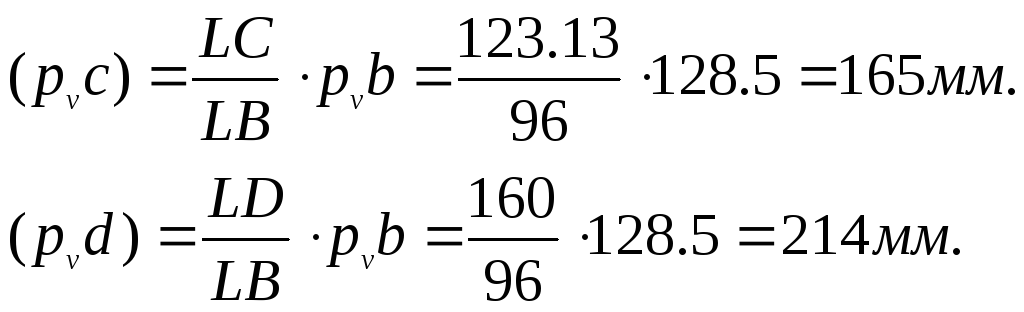
Скорость точек С и D равна

Скорость точки C₅ определяем из уравнения

Уравнение решаем графически. Для этого из точки с₃ проводим вектор, параллельно звену LD. Из полюса проводим линию, параллельную движению ползуна и в точке пересечения находим точку с₅.

Скорости равны

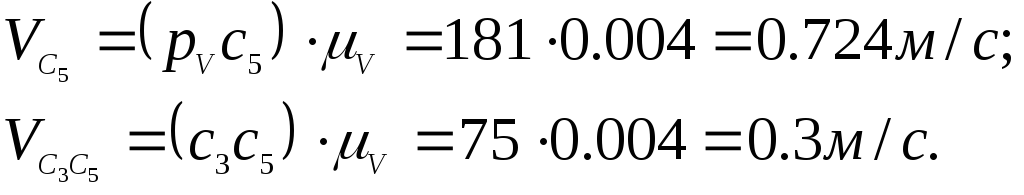
Угловые скорости равны

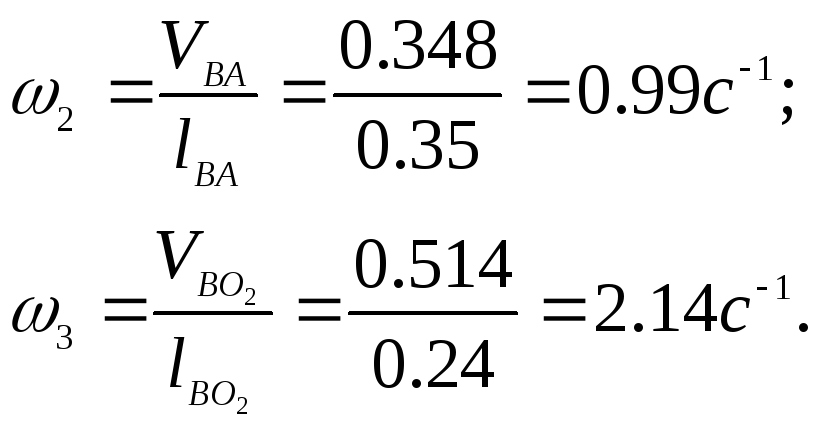
Положение центра масс звеньев находится на их середине.

Скорости равны.

2.5 Построение плана ускорений

Ускорение точки А определяем с уравнения

где w₀ – ускорение точки О=0, так как она неподвижна;

нормальное ускорение точки А. Его величина

тангенциальное ускорение точки А=0, так как ε₁=0.

Выбираем положение точки Р_w – полюс и проводим вектор нормального ускорения точки А.

Масштабный коэффициент плана ускорений:

Ускорение точки В определяем с системы уравнений

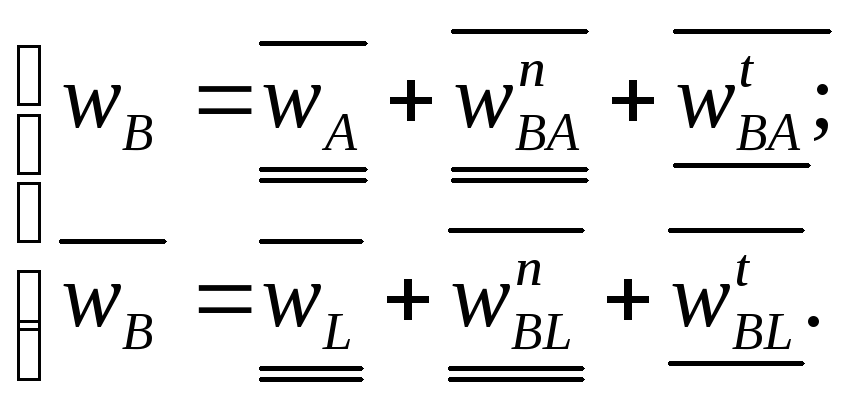
_{Определяем значения нормальных ускорений}

_{Определяем длину векторов нормальных ускорений}

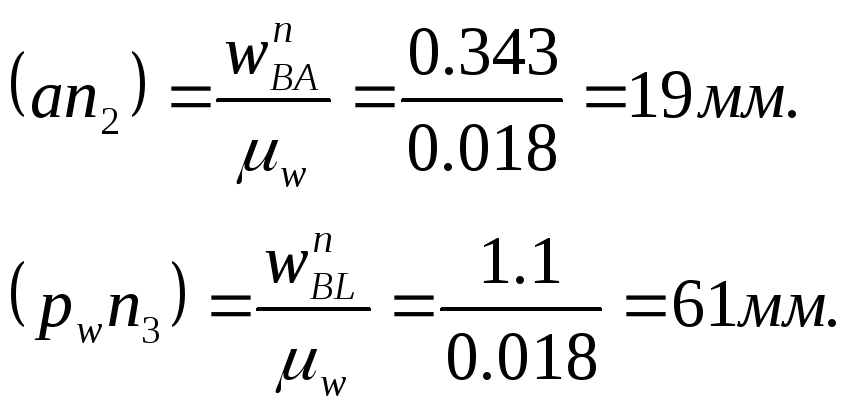
Графически решаем данную систему. Для этого из точки а проводим вектор нормального ускорения параллельно звену ВА. Из точки р_w проводим вектор нормального ускорения параллельно звену ВL. С концов нормальных ускорений проводим тангенциальные ускорения перпендикулярно нормальным и в точке пересечения получаем точку b и определяем ускорения

Положение точек С и D определяем с соотношения

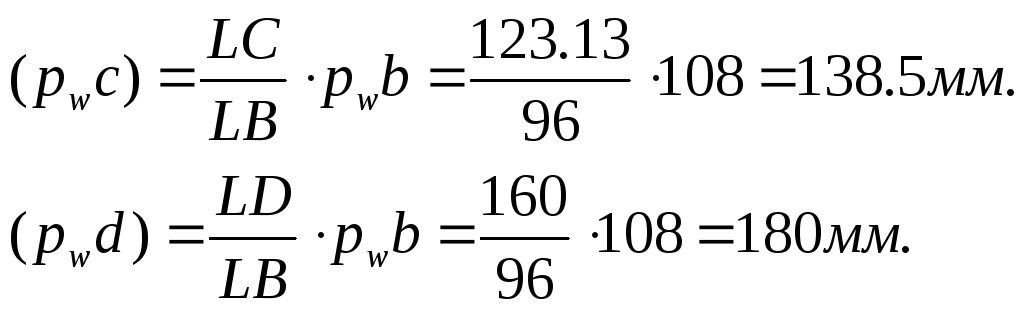
Ускорение точек равно

Ускорение точки С₅ определяем из уравнения

Определяем величину кориолисово ускорения

_{Определяем длину вектора ускорения}

Уравнение решаем графически. Для этого из точки с₃ проводим вектор кориолисового ускорения. С точки К проводим перпендикуляр до пересечения с горизонталью, которая проведена из полюса.

Ускорения равны

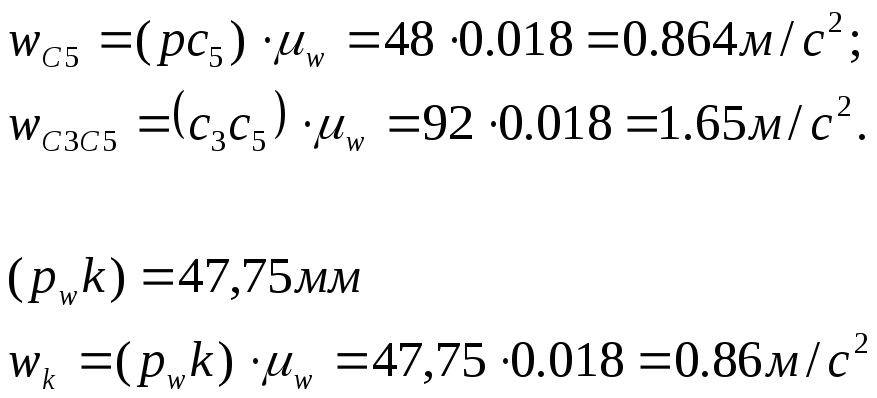
Положение центра масс звеньев находится по середин центра масс.

Ускорения равны.

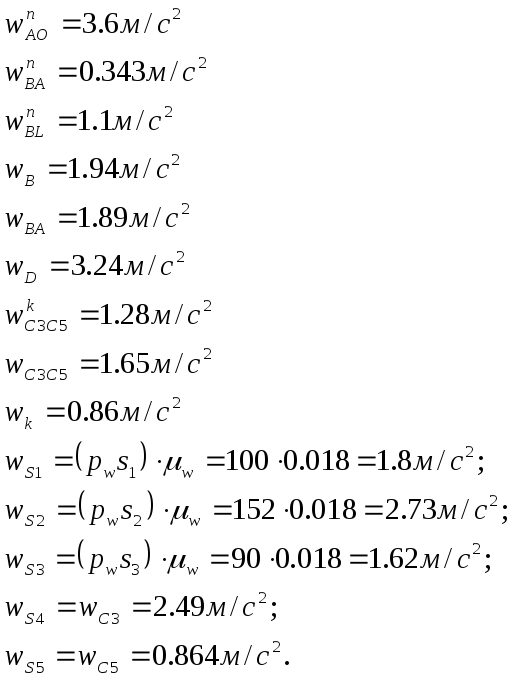
Положение центра масс звеньев находится по середин центра масс.

Определяем тангенциальные ускорение:

Угловые ускорения

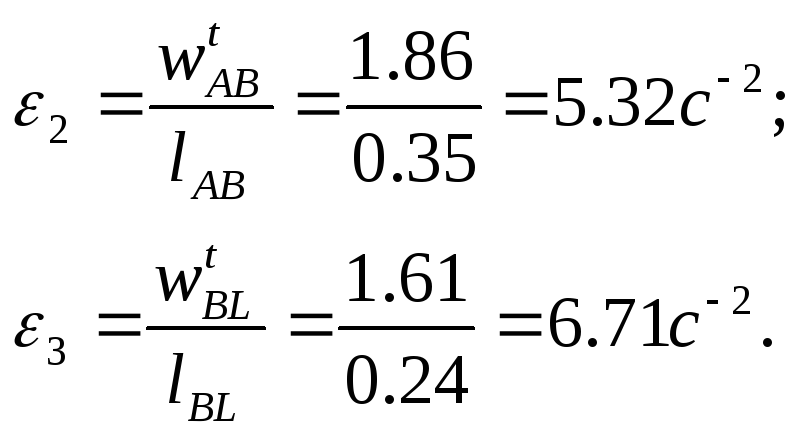
3 Силовой анализ

Для начала составим расчётную модель для проведения силового анализа, которая представляет собой кинематическую схему механизма

Массы планок равны

Вектор силы тяжести выходит из точки центра масс звена и направляется вертикально вниз.

Далее рассчитаем величины сил инерции по следующей формуле:

,

где – ускорение центра масс звена, которое определяется на плане ускорений механизма.

Подставляя найденные значения ускорений центров масс в формулу для определения силы инерции, получаем:

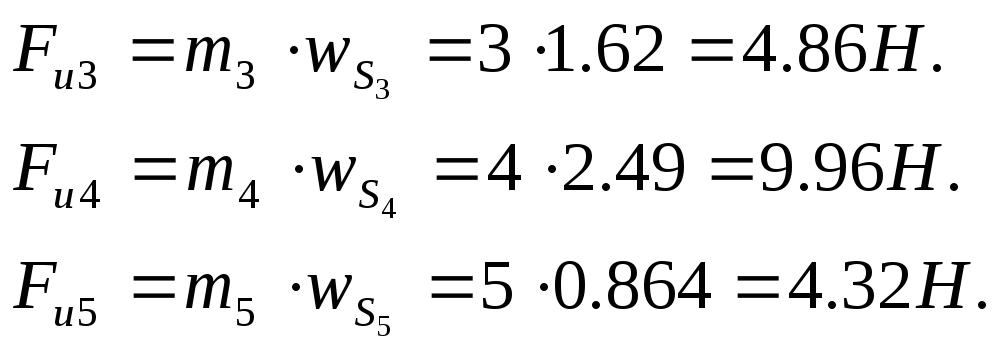
Вектор силы инерции выходит из точки и направляется в противоположную сторону вектору ускорения центра масс звеньев , т.е. .

Далее рассчитаем моменты пар сил инерции звеньев. Данный силовой фактор направлен в противоположную сторону угловому ускорению звена () и определяется по следующей зависимости:

,

где  – момент инерции звена относительно оси, проходящей через центр масс;  – угловое ускорение звена.

Момент инерции ведомых линейных звеньев определяем по формуле:

Тогда моменты инерции и моменты пары сил инерции для звеньев в исследуемом плоском рычажном механизме будут равны:

Вначале выделяем из состава схемы группы звеньев. Исследуемый механизм состоит из трех групп: первичный механизм 0-1, структурная группа звеньев 2-3 и структурная группа звеньев 4-5 (см. структурный анализ). Каждую группу вычерчивают отдельно в произвольном масштабном коэффициенте длин , начиная с той, в которую входит выходное звено. Далее с расчётной модели переносят все силы, действующие на звенья группы, а отброшенные связи с другими звеньями механизма заменяют реакциями. Во вращательной паре отброшенная связь заменяется реакцией, которая раскладывается на две составляющие: и   нормальная и тангенциальная реакции соответственно. Вектор всегда направлен вдоль оси звена (параллельно), а вектор  перпендикулярно оси звена.

Рассмотрим структурную группу 4-5. К данной группе приложены сила инерции и массы звеньев. Также приложена сила сопротивления. Которая равна

Запишем уравнение равновесия суммы всех сил по группе 4-5

Равенство нулю векторной суммы означает, что многоугольник сил является замкнутым.

Принимаем масштабный коэффициент _F = 127 Н/мм и определяем длинны векторов реакций

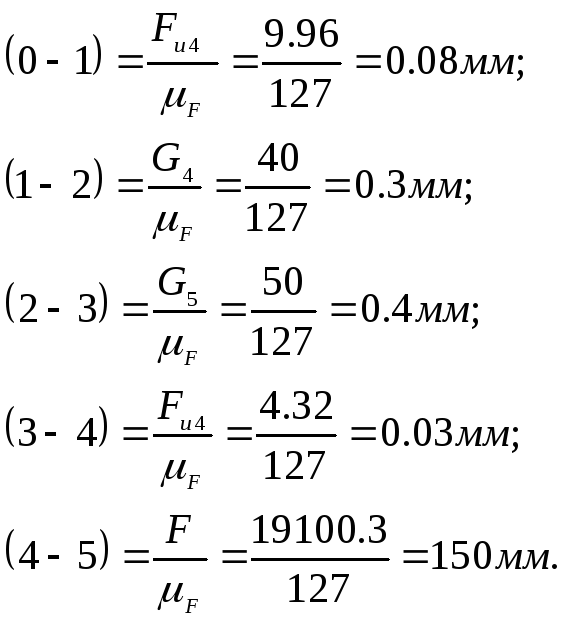
Переходим к построению векторного многоугольника сил. На чистом месте строим линию, на которой лежит вектор (перпендикулярно оси коромысла). Так как размер вектора нам пока неизвестен, то произвольно на данной прямой ставим точку и уславливаемся, что она будет являться вершиной искомого вектора . Далее в сумме идут вектора известных сил по величине и направлению, поэтому их по порядку строим. При этом каждый последующий в сумме вектор строится из вершины предшествующего. При длине вектора меньше 1 мм его не оказываем на чертеже. Построив вектор , из его вершины, строим линию действия неизвестной реакции и .

Найдём величины искомых реакций, замерив их на многоугольнике и умножив на :

Вычертим отдельно структурную группу 2-3 и показываем все силы, действующие на звенья данной группы. Отброшенные связи шатуна с кривошипом и коромысла со стойкой, по принципу освобождаемости от связей, заменим реакциями и соответственно. В данной структурной группе имеется четыре неизвестных и , значит система трижды статически неопределима.

В первую очередь определяем тангенциальные реакции, составляя уравнения равновесия .

Для определения величины рассмотрим отдельно второе звено и составим для него уравнение равновесия, получим:

Тогда будет равна:

Знак плюс в полученном значении означает, что взятое ранее направление вектора реакции выбрано нами верно.

Для определения величины рассмотрим отдельно кулису и составим для него уравнение равновесия, получим:

Тогда будет равна:

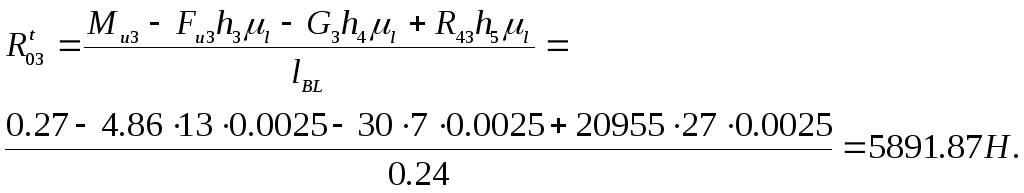
Знак плюс в полученном значении означает, что взятое ранее направление вектора реакции выбрано нами верно.

В структурной группе 2-3 осталось две неизвестных силы (), их можно определить построением векторного многоугольника сил. Составляем уравнение равновесия , по которому будем строить многоугольник.

Тогда для СГ 2-3 будем иметь:

.

Равенство нулю векторной суммы означает, что многоугольник сил является замкнутым.

Принимаем масштабный коэффициент _F = 105 Н/мм и определяем длинны векторов реакций

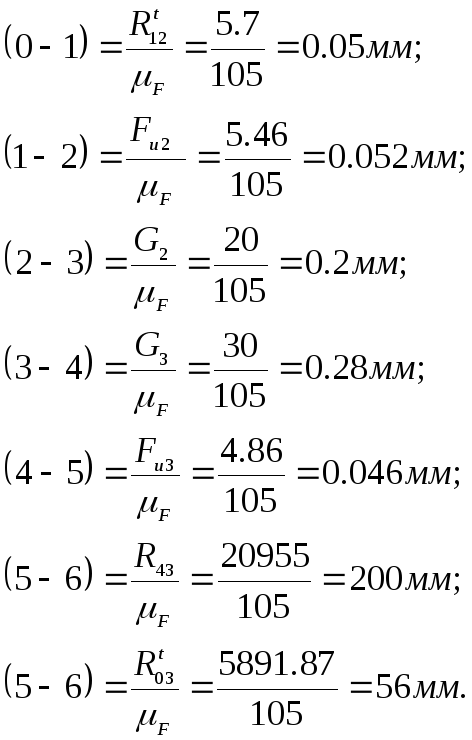
Переходим к построению векторного многоугольника сил. На чистом месте строим линию, на которой лежит вектор (параллельно оси шатуна). Так как размер вектора нам пока неизвестен, то произвольно на данной прямой ставим точку и уславливаемся, что она будет являться вершиной искомого вектора . Далее в сумме идут вектора известных сил по величине и направлению, поэтому их по порядку строим. При этом каждый последующий в сумме вектор строится из вершины предшествующего. Поострив вектор , из его вершины, строим линию действия неизвестной реакции (параллельно оси коромысла). При этом линии действия векторов и пересекаются, замыкая многоугольник сил и определяя действительные направления данных векторов и их модули.

Найдём величины искомых реакций, замерив их на многоугольнике и умножив на :

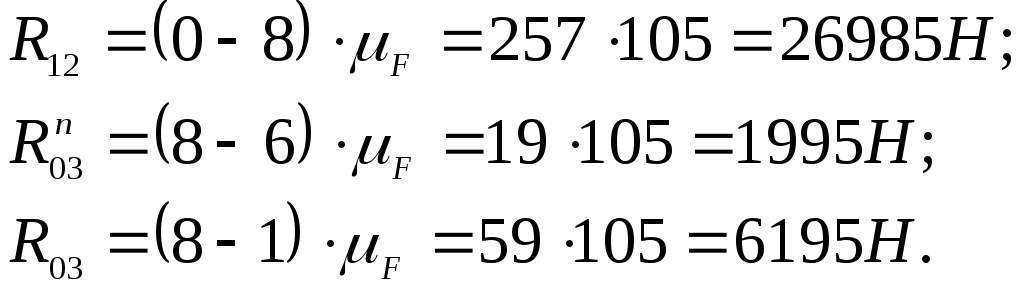
Вычертим следующую группу звеньев (первичный механизм 0-1). Покажем все силы, действующие на звенья данной группы. Отброшенную связь кривошипа с шатуном заменим реакцией , которая по модулю равна , но в противоположную сторону направлена, т.е. . Следовательно, из предшествующего многоугольника сил берём вектор , переносим его в точку A на кривошипе и в противоположную сторону направляем , тем самым найдём направление реакции .

Определим уравновешивающий момент

В первичном механизме осталась одна неизвестная реакция . Чтобы её найти построим векторный многоугольник сил.

Запишем уравнения равновесия всех сил по группе

Принимаем масштабный коэффициент _F =180 Н/мм и определяем длинны векторов реакций

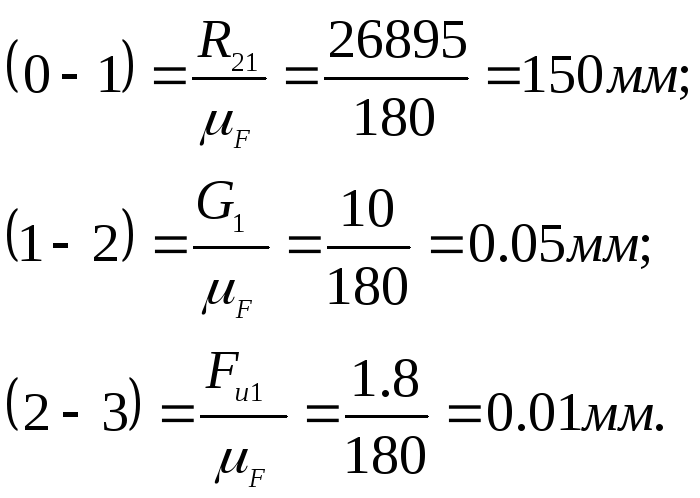
Найдём величину искомой реакций, замерив ее на многоугольнике и умножив на :