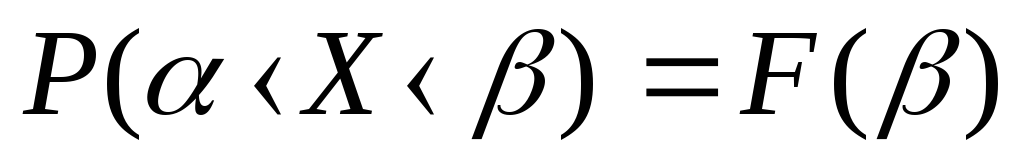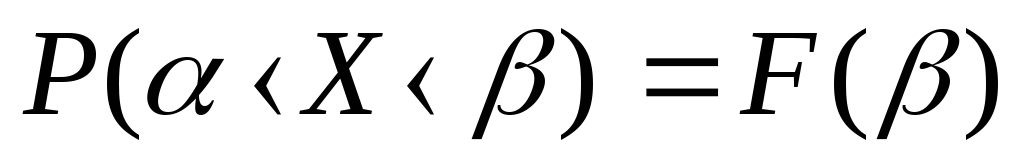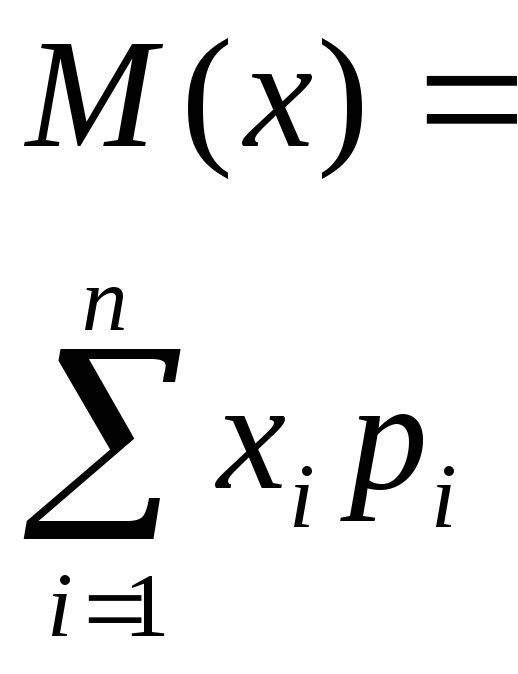- •Тема 2. Схема незалежних випробувань
- •Тема 3. Випадкові величина та числові характеристики випадкових величин
- •Тема 4. Закони розподілу випадкових величин
- •Тема 5. Первинне опрацювання статистичних даних і.
- •Тема 6. Оцінювання параметрів розподілу
- •Тема 7. Перевірка статистичних гіпотез
- •Тема 8. Елементи теорії кореляції і регресії
- •Тема 9. Елементи дисперсійного аналізу
|
Вірогідною |
Випадковою |
Неможливою |
Сумісною |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,5 |
0,08 |
1 |
|
незалежні |
залежні |
неможливі |
вірогідні |
|
0 |
1 |
-1 |
|
|
1 |
-1 |
0 |
∞ |
|
Незалежні |
Залежні |
Сумісні |
Несумісні |
|
Сумісні |
Несумісні |
Вірогідні |
неможливі |
|
2 |
3 |
1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
0 |
|
0,15 |
1,5 |
0,56 |
0,75 |
|
Поява події А впливає на ймовірність появи події В |
Поява однієї з них не впливає на ймовірність появи іншої події |
Поява
події А впливає на ймовірність
протилежної події
|
Поява
події В впливає на ймовірність події
|
|
поява події А впливає на ймовірність появи події В |
поява однієї з них не впливає на ймовірність появи іншої події |
поява
події А впливає на ймовірність
протилежної події
|
поява
події В впливає на ймовірність події
|
|
|
|
|
|
|
0 |
1 |
-1 |
|
|
0 |
1 |
-1 |
|
|
до залежних |
до вірогідних |
до неможливих |
до незалежних |
|
Настає з одночасним настанням події А і В |
Настає з настанням події А |
Настає з настанням події В |
Настає з настанням події А і ненастанням події В |
|
настає тільки з однієї події |
не настає з одної події |
настає з одночасним настанням обох події |
є неможливою подією |
|
Незалежні |
Залежні |
Сумісні |
Несумісні |
|
1 |
-1 |
|
|
|
Сумісні |
Несумісні |
Залежні |
Незалежні |
|
4 |
6 |
8 |
12 |
|
19 |
5 |
3 |
1 |
|
12 |
16 |
4 |
24 |
|
1, 5, 11 |
5, 10 |
5 |
10 |
|
|
|
|
|
|
7 |
4, 9 |
2, 6 |
6 |
|
0 |
|
|
1 |
|
|
|
|
|
|
0,92 |
0,81 |
0,2 |
0,1 |
|
якщо її не можна розкласти на елементарні події |
якщо її можна розкласти на елементарні події |
якщо вона є вірогідною |
якщо вона є неможливою |
|
Поява події А впливає на ймовірність появи події В |
Поява однієї з них не впливає на ймовірність появи іншої події |
Поява
події А впливає на ймовірність
протилежної події
|
Поява
події В впливає на ймовірність події
|
|
|
|
|
|
|
|
|
|
|
|
коли вони невідомі |
коли їх можна перелічити |
коли відомі, але не всі |
коли відомий хоча б один елемент |
|
1,2,4,6 |
1,3,6 |
4,6 |
3,6 |
|
|
|
|
|
|
2 |
4 |
6 |
8
|
|
гг, цц, гц, цг |
гг, гг, цц, цц |
гц, гц, цг, цг |
ц, г, г, ц |
|
неможлива |
незалежна |
випадкова |
вірогідна |
|
|
|
|
|
|
0 |
5 |
1 |
0,2 |
|
8 |
6 |
4 |
3 |
|
0 |
1 |
3 |
0,3 |
|
2 |
4 |
8 |
16 |
|
цггц, ццгц |
цццц, цццг, ццгц |
цгцг, ццгг, цггц |
гггг, гггц, ггцг, цггг |
|
залежна |
неможлива |
вірогідна |
випадкова |
|
1 |
|
|
|
|
Сумісні |
Несумісні |
Залежні |
Незалежні |
|
2, 4 |
3, 6 |
2, 3, 4, 6 |
2, 4, 6 |
|
1 |
0,5 |
0,1 |
0,001 |
|
кількісної ознаки |
якісної ознаки |
функції розподілу |
щільності розподілу |
|
кількісної ознаки |
якісної ознаки |
функції розподілу |
щільності розподілу |
|
|
|
|
|
|
Ні |
Так |
Утворюють при певних умовах |
Для позитивного твердження недостатньо даних |
|
0,1 |
0,2 |
0,3 |
0,4 |
|
Настає з одночасним настанням події А і В |
Настає з настанням події А і одночасним ненастанням події В |
Настає з настанням події В і ненастанням події А |
Настає з ненастанням одночасно і події А і події В |
|
сумісна |
випадкова |
неможлива |
вірогідна |
|
10 |
2 |
1 |
8 |
|
1 |
2 |
|
|
|
Не може |
Може, якщо х вимірюється в метрах |
Може в окремих випадках |
Не може коли ймовірність дорівнює нулю |
|
Математичним сподіванням |
Дисперсію |
Ймовірністю події |
Коефіцієнтом кореляції |
|
|
|
|
|
|
0 |
-1 |
1 |
∞ |
|
|
|
|
|
|
|
А |
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ймовірність події В при умові, що здійснилась подія А |
ймовірність події А при умові, що здійснилась подія В |
ймовірність події А |
ймовірність події В |
|
рівними |
протилежними |
однаковими |
подібними |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(A/B)= |
P(A/B)= |
P(A/B)= |
|
1 |
2 |
3 |
4 |
|
неперервний обмежений |
дискретний необмежений |
неперервний |
дискретний обмежений |
|
залежними |
незалежними |
вірогідними |
неможливими |
|
Сумісними |
Несумісними |
Залежними |
Незалежними |
|
Сумісними |
Несумісними |
Залежними |
Незалежними |
|
Сумісні |
Залежні |
Незалежні |
несумісні |
|
Сумісні |
Несумісні |
Залежні |
Незалежні |
|
|
|
|
|
|
0 |
1 |
-1 |
∞ |
|
|
|
|
|
|
|
|
|
|
|
безумовною |
умовною |
геометричною |
статистичною |
|
сумісні |
не сумісні |
залежні |
незалежні |
|
найменшою |
вірогідною |
неперервною |
дискретною |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сумісні |
Несумісні |
Залежні |
Незалежні |
|
|
|
|
|
|
|
|
|
|
Тема 2. Схема незалежних випробувань
|
|
|
(-∞,∞) |
[-1, 1] |
[-3, 4] |
[-4, 4] |
|---|---|---|---|---|---|
|
З’явилась рівно n разів в m незалежних випробуваннях |
З’явилась рівно m разів в n незалежних випробуваннях |
З’явилась m разів і не з’явилась n-m разів в m незалежних випробуваннях |
З’явилась n+1 раз в m незалежних випробуваннях |
|
|
|
|
|
|
|
|
|
|
|
незалежні випробування за схемою Бернуллі |
залежні сумісні випробування |
залежні несумісні випробування Бернуллі |
Попарно сумісні випробування Бернуллі |
|
Якщо кожне випробування має два несумісні наслідки зі змінними ймовірностями рі і qі |
Якщо кожне випробування має два сумісні наслідки |
Якщо кожне випробування має лише два несумісні наслідки зі сталими ймовірностями р і q |
Якщо кожне випробування має лише один наслідок з ймовірністю Р = 1 |
|
|
|
|
|
|
|
|
|
|
|
Бернуллі |
Муавра-Лапласа |
Пуассона |
Лапласа |
Тема 3. Випадкові величина та числові характеристики випадкових величин
|
Величина набуває лише значення 10 |
Величина набуває того чи іншого скінченого числового значення з певною ймовірністю |
Величина є множиною можливих значень, яка незчисленна |
Величина набуває того чи іншого можливого числового значення |
|
незалежні |
залежні |
сумісні |
несумісні |
|
у вигляді формули |
у вигляді таблиці |
у вигляді графіка |
у вигляді діаграми
|
|
м2 |
м |
м-1 |
кг. |
|
Кг. |
(кг)2 |
(кг)-1 |
М2 |
|
0 |
1 |
-1 |
2 |
|
0 |
1 |
2 |
3 |
|
1,5 |
1 |
0 |
-1,5 |
|
неможливі |
вірогідні |
незалежні |
залежні |
|
математичне сподівання відхилення випадкової величини |
математичне сподівання квадрата відхилення випадкової величини від його математичного сподівання |
різниця відхилень випадкової величини |
інша відповідь |
|
нулю |
одиниці |
нескінченності |
будь-якому числу |
|
0 |
1 |
-1 |
∞ |
|
для вірогідних подій |
для неможливих подій |
для малоймовірних подій |
для складеної події |
|
сумісні |
несумісні |
залежні |
незалежні |
|
якщо експеримент відбувається не за схемою Бернуллі |
якщо простір елемент. подій містить для одного експерименту три несумісних події |
якщо кожний експеримент має лише дві несумісні події |
якщо у кожному експерименті випадкова подія є неможливою |
|
0,1 |
0,2 |
0,3 |
0,4 |
|
0,1 |
0,2 |
0,3 |
0,4 |
|
випадковими величинами |
ймовірностями випадкових величин |
значенням випадкової величини |
можливими значеннями випадкової величини та їх ймовірностями |
|
класичною |
геометричною |
безумовною |
умовною |
|
залежною |
незалежною |
вірогідною |
неможливою |
|
залежною
|
неможливою |
випадковою |
вірогідною |
|
|
|
|
|
|
|
|
|
|
|
яка з’явилась рівно n-разів в m-випробовуван-нях |
з’явилась рівно m-разів в n-випробовуваннях |
з’явилась n-m разів |
з’явилась n+1 раз в n-випробовуваннях |
|
|
|
|
|
|
Величина набуває лише значення 10 |
Величина набуває того чи іншого скінченого числового значення з певною ймовірністю |
Величина є множиною можливих значень, яка незчисленна |
Величина набуває того чи іншого можливого числового значення |
|
|
|
|
|
|
не можна |
можна |
можна умовно назвати |
ваша відповідь |
|
|
|
|
|
|
|
|
|
|
|
дискретною |
неперервною |
елементарною |
складеною |
|
нульове значення ймовірності |
середня ймовірність появи |
мінімально ймовірність появи |
найбільша ймовірність появи |
|
0 |
1 |
∞ |
-∞ |
|
0,4 |
0,3 |
0,2 |
0,1 |
|
залежні |
незалежні |
сумісні |
несумісні |
|
0 |
10 |
8 |
1 |
|
1 |
2 |
3
|
4 |
|
|
|
|
|
|
модою випадкової величини |
медіаною випадкової величини |
математичним сподіванням |
корінь квадратний з дисперсії |
|
|
|
|
|
|
дискретну |
неперервну |
елементарну |
складену |
|
рівно n-раз |
рівно m-раз |
не більше m-разів |
не більше n -разів |
|
0,4 |
0,5 |
0,6 |
0,7 |
|
може |
не може |
даних недостатньо |
інша відповідь |
|
не може |
може |
можне, якщо подія А вірогідна |
може, якщо подія А неможлива |
|
1 |
0,5 |
-1 |
0 |
|
збільшення випадкової величини |
значення випадкової величини |
міру розсіювання випадкової величини |
зменшення випадкової величини |
|
Найбільша частота ознаки |
Значення ознаки з найбільшою частотою |
Значення ознаки з найменшою частотою |
Серединне значення ознаки |
|
Ймовірність
обчислення середньої вибіркової
|
Ймовірність, з якою обчислюється вибіркова дисперсія S2 |
Ймовірність, з якою довірчий інтервал покриває оцінюваний параметр генеральної сукупності |
Ймовірність того, що подія А здійсниться |
|
квадрат відхилення випадкової величини |
відхилення випадкової величини |
центр розсіювання випадкової величини |
асиметрію випадкової величини |
|
Задати послідовність всіх можливих значень випадкової величини х та відповідні їм ймовірності |
Задати деякі можливі значення випадкової величини х та відповідні їм ймовірності |
Задати всі можливі значення випадкової величини х |
Задати ймовірності випадкової величини х |
|
Пуасонівський |
Експоненціальний |
Нормальний |
Стьюдента |
|
|
|
|
|
|
Такого розподілу не буває. |
Розподіл, який немає моди |
Розподіл з двома модами |
Розподіл з однією модою |
|
|
|
|
|
|
сумісними |
попарно-несумісними |
залежними |
вірогідними |
|
залежною
|
незалежною |
неможливою |
вірогідною |
|
|
|
|
|
|
1 |
-1 |
0 |
0,5 |

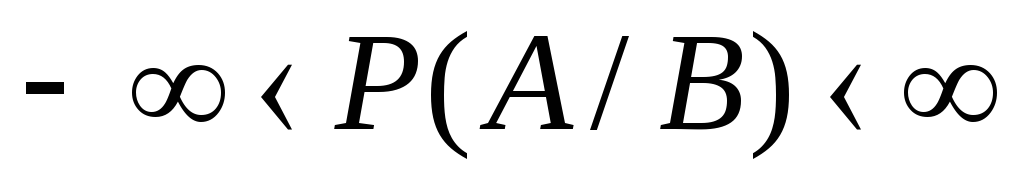
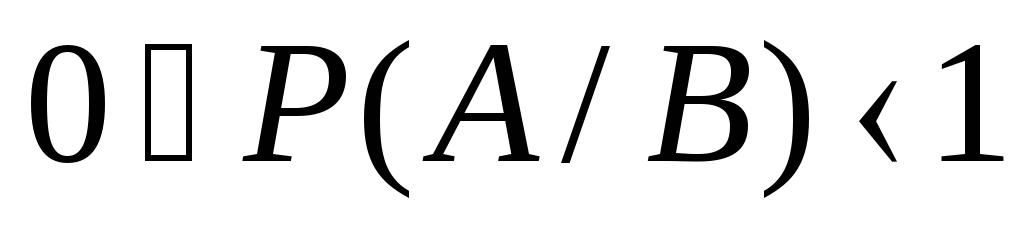
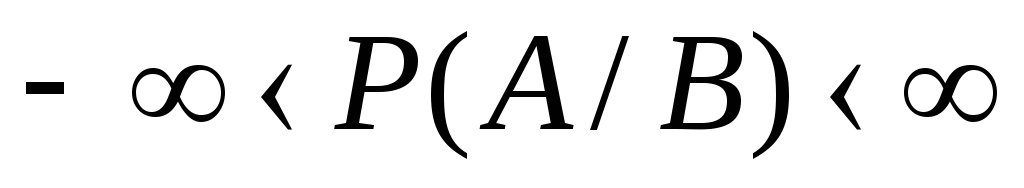




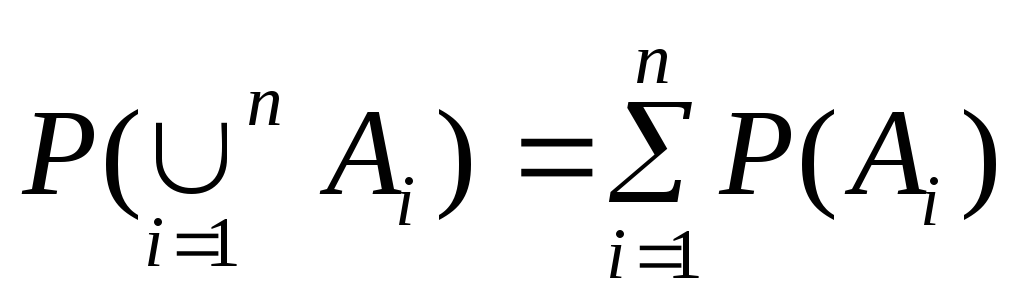
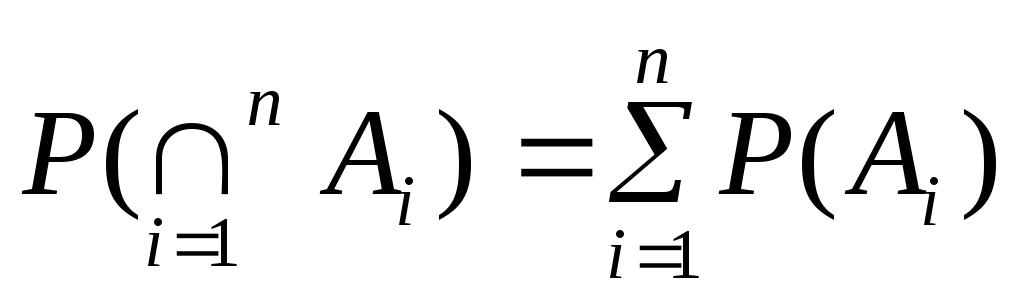
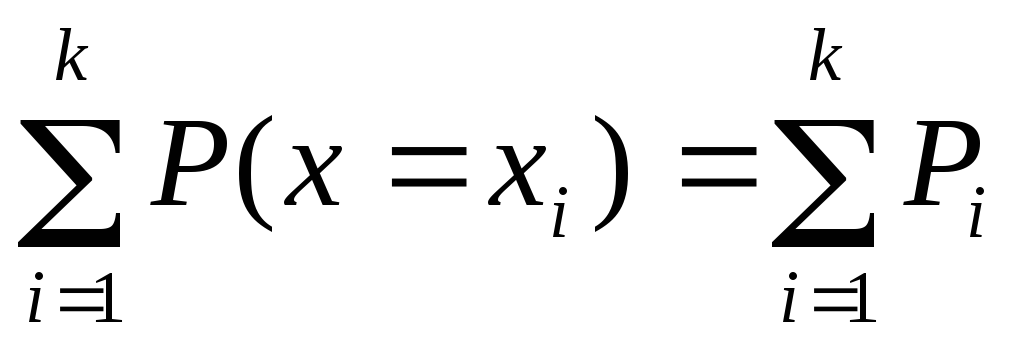 . Чому вона дорівнює?
. Чому вона дорівнює? ,
де f(х)
є щільність ймовірності випадкової
величини Х. Чому дорівнює ця ймовірність?
,
де f(х)
є щільність ймовірності випадкової
величини Х. Чому дорівнює ця ймовірність?