Глава 3. Иерархическая структура и математические модели эмс рэс

Теоретический анализ ЭМС РЭС возможен только при наличии соответствующих математических моделей, входящих в её состав элементов.

Математические модели ЭМС РЭС и методы анализа ЭМС существенно зависят от уровня иерархии ЭМС РЭС. Принятая иерархическая структура ЭМС РЭС соответствует иерархии, установленной в радиотехнике, и содержит следующие уровни:

- ЭМС элементов цепей и узлов

- ЭМС устройств и блоков (приёмник, передатчик, антенно-фидерные устройства);

- ЭМС отдельных систем и станций;

- ЭМС комплексов РЭС.

Первые три уровня относятся к внутрисистемной ЭМС и обеспечиваются соответствующими схемно-конструктивными мерами на этапе проектирования и разработки конкретной РЭС.

Четвёртый уровень связан с межсистемной ЭМС различных РЭС. Она не всегда может быть обеспечена только за счёт совершенства отдельных РЭС. Особенно это относится к бортовым комплексам и в этом плане требуется системный подход к анализу и методам обеспечения ЭМС комплексов РЭС.

На всех уровнях для анализа ЭМС требуется знание электромагнитной обстановки (ЭМО) в месте расположения объекта. В настоящее время существуют три подхода для описания ЭМО: электродинамический, энергетический, вероятностный.

I. Электродинамический наиболее сложен и полон и заключается в расчете в требуемой области пространства суммарного электромагнитного поля от всех источников. То есть в t-ой системе надо опреде­лить поля от всех N систем на произвольной частоте f , а затем их просуммировать

(3.1)

Для расчёта напряжения сигнала, возникающего на выходе t-ой приёмной антенны под действием напряжённости можно использовать аппарат матриц рассеяния [ S ] описанный в § 2.3.

2. Энергетический метод. При этом в t-ой системе ищутся не поля, а мощности помехи и сигнала. Затем рассчитывается отношение сигнал/помеха P_c/P_п на входе приёмного устройства t-ой РЭС. При этом для конкретной РЭС всегда можно указать пороговое значение

K_пор = (P_c/P_п)_min , превышение которого обеспечит ЭМС. А условие обеспечения ЭМС t-ой РЭС в комплексе будет иметь вид

P_{c t} /( P_{п t} + P_{m t} ) ≥ ( P_c/P_п )_{min t} = K_пор (3.3)

где P_{m t} - эквивалентная мощность шумов на входе t-ого приёмника в полосе его пропускания.

Для расчета отношения сигнал/помеха используются две модели РЭС в комплексе:

- модель дифференциального вклада (МДВ),

- модель интегрального вклада (МИВ).

МДВ предполагает, что имеется ограниченное число РЭС, взаимовлияющих друг на друга. Причём известны энергетические спектры W_s(f) каждого передатчика и коэффициент связи _ts антенных устройств t-ой и s-ой РЭС (рис.3.1).

При этих условиях мощность помехи на входе t-ого приемника от излучения s-ой РЭС равна

(3.3)

причем интегрировать необходимо по всей области частот, в которой W_s(f) отлична от нуля.

Полностью мощность помехи на входе t-ого приёмника равна:

(3.4)

Мощность полезного сигнала на входе t-ого приёмника можно найти по формуле

(3.5)

где S_{t t}(f) - коэффициент передачи по рабочей трассе от выхода t-ого передатчика до входа t-ого приёмника, 2∆f_осн – полоса основного канала.

ЭМС всего комплекса РЭС считается обеспеченной, если для каждой РЭС

P_{c t} /( P_{п t} + P_{m t} ) > K_{пор t} ; ( t = 1, 2, … N ) (3.6)

Вычисление приведённых выше интегралов представляет определённые трудности, поэтому и используют аппроксимацию входящих в них функций.

Наибольшую опасность представляют три ситуации перекрытия по частоте:

- основного излучения s-ого передатчика и основного t-ого

приёмника;

- основного излучения s-ого передатчика и неосновных каналов

приёма t-ого приёмника;

- неосновного излучения s-ого передатчика и основного канала

t-ого приёмника.

Введём обозначения:

- полосы основного и неосновного каналов приёма t-ого приёмника;

- полосы основного и неосновного излучений передатчика с номером s.

- коэффициенты перекрытия основной и неосновной полос приёма с основной или неосновной полосой излучения.

Тогда мощность на входе t-ого приёмника в основной полосе от s-ого передатчика будет равна

(3.7)

где через и обозначены средние значения величин в полосе ;

- средняя мощность передатчика s в полосе f _t .

А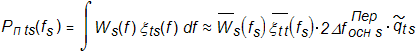налогично мощность на входе t-ого приёмника в основной полосе излучения s-ого передатчика равна

(3.8)

До сих пор предполагалось, что для каждой РЭС известно значение K_пор, входящее в (3.6).

Если же известны характеристики многоканальной избирательности L _t (f) всех t = 1, 2,… N приёмников, входящих в комплекс, то возможно построение нелинейной модели дифференциального вклада.

При этом ЭМС будет обеспечена, если будут выполняться следующие системы неравенств

(3.9)

Первая система неравенств обеспечивает ЭМС по основному каналу приёма, вторая – по неосновным.

Смысл этих двух систем неравенств проще всего понять из их геометрической интерпретации (рис.3.2).

На рис.3.2(а),(б) изображены многочастотная ХЧИ приёмника t и энергетический спектр передатчика s соответственно. На рис.3.2(в) изображена ситуация, при которой ЭМС обеспечена как по основному каналу приема, так и по побочным каналам. На рис.3.2(г) приведён пример ситуации, при которой ЭМС по этим каналам не обеспечивается (соответствующие частотные полосы заштрихованы).

Модель интегрального вклада (МИВ) используется тогда, когда число мешающих сигналов неизвестно и предполагается, что они распределены в пространстве непрерывно.

Тогда мощность помех на входе t-го приёмника

(3.10)

p_{п t} - объемная плотность помехи.

3. Вероятностный метод позволяет получить вероятностную оценку отношения сигнал/помеха. В этом случае мощность помехи и направле­ние ее прихода считаются случайными величинами с известными закона­ми распределения. Часто используют нормальный закон с плотностью распределения

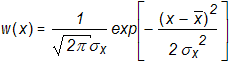(3.11)

или логарифмический нормальный закон с плотностью распределения

(3.12)

(Используется для величин, выраженных в децибелах).

Рассмотрим далее модель дифференциального вклада.

В децибельном масштабе выражение (3.7) запишется в виде

(3.13)

Каждое из слагаемых распределено по нормальному закону. Учитывая свойства нормального закона, получаем, что среднее значение мощности помехи

(3.14)

а её дисперсия

(3.15)

Аналогично и для отношения сигнал/помеха в децибельном масштабе, получим

(3.16)

В силу центральной предельной теоремы результирующий закон распределения w (сигнал/помеха) является нормальным, поэтому вероятность превышения величиной сигнал/помеха порогового значения

, определяющая вероятность ЭМС, вычисляется следующим образом

(3.17)

где

- табулированный интеграл вероятности.