3.2.2. Определение размеров косозубого колеса

Как это видно из рис.3.2б, окружной и нормальный шаги косозубого колеса связаны зависимостью:

, (3.9)

где β – угол наклона зубьев, который рекомендуется принимать в пределах , во всяком случае, не более . При делении членов уравнения (3.9) на число π получим значение нормального модуля: . (3.10)

Соответственно, диаметры делительных окружностей колес, выраженные через нормальный модуль, составят:

; . (3.11)

Межцентровое расстояние:

, (3.12)

откуда расчетное значение нормального модуля:

. (3.13)

Полученное значение нормального модуля следует округлить в соответствии со стандартными рядами ГОСТ 9563-80 – .

При подстановке стандартного значения модуля в формулу (3.10) межцентровое расстояние не только изменится, но и, возможно, будет выражаться дробной величиной, что недопустимо. Поэтому, оставляя неизменными модуль и межцентровое расстояние, приходится корректировать угол наклона зубьев β. Из формулы (3.13) имеем:

. (3.14)

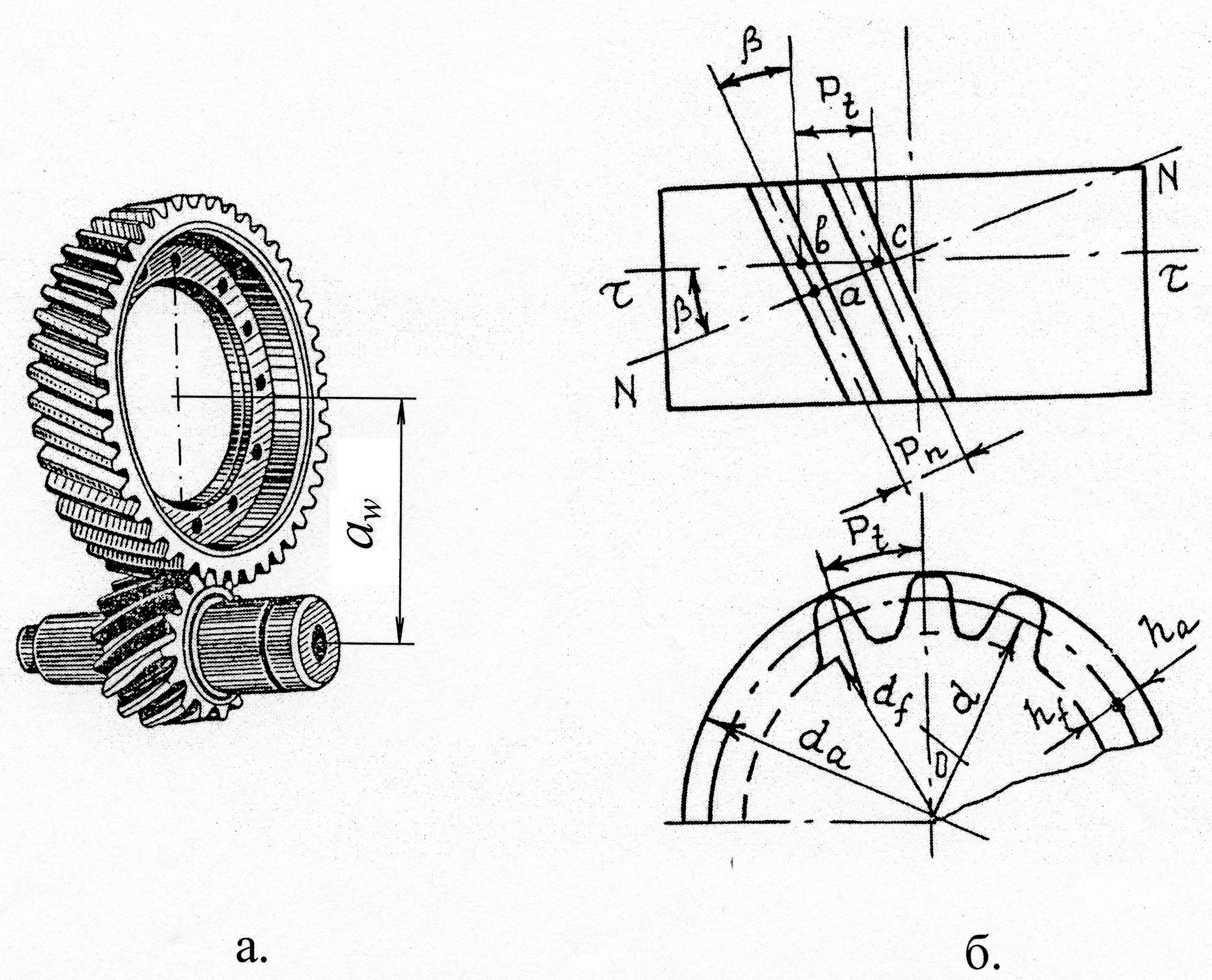
Рис. 3.2

Прочие размеры косозубого колеса вычисляют, приняв , . В результате имеем диаметры окружностей выступов и впадин колеса: ; . (3.15) Ширина колеса: , шестерни – . (3.16)

Пример 2.3.

Найти размеры косозубых колес по тем же данным, что и в примере 1.3: Нмм, , МПа.

Находим межцентровое расстояние передачи по формуле (3.1), приняв и :

мм.

Нормальный модуль следует выбрать в пределах 1,5…3,0 мм. Принимаем мм. Далее выберем угол наклона зубьев () и определяем число зубьев шестерни. Из (3.13) имеем:

.

Принимаем и корректируем угол наклона зубьев. Из выражения (3.14): 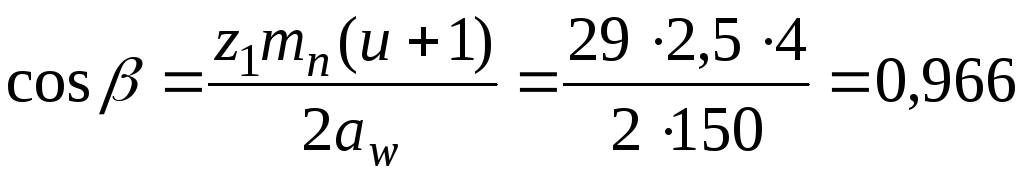, откуда .

Число зубьев колеса . Параметры передачи в мм находим по формулам (3.11), (3.15), (3,16): ;

; ;; ; .

Межцентровое расстояние: мм – верно!

Ширина колеса: мм , шестерни – мм.

3.2.3. Проверка контактных напряжений

Проверку контактных напряжений в спроектированной передаче следует производить в следующем порядке.

1) Определяем степень точности передачи в зависимости от размеров колес и окружных скоростей на зубчатом венце:

(м/c), (3.16)

где – скорость входного вала редуктора (ротора двигателя ), м/c;

– диаметр шестерни, м. Степень точности передачи определяется по таблице 3.1.

Таблица 3.1

Степень точности по ГОСТ 1643-81	Прямозубые Колеса	Косозубые Колеса
6-я – повышенная степень точности	м/c	м/с
7-я – нормальная степень точность	м/c	м/c
8-я – пониженная степень точности	м/c	м/c

В соответствии с приведенной таблицей, а также учитывая, что передачи общего машиностроения не требуют особой (высокой) точности, принимают обычно 7-ю или 8-ю степень точности.

2) Определяем коэффициент ширины шестерни по диаметру

, (3.17)

где ширина шестерни, – диаметр ее начальной окружности.

3) Производим проверка контактных напряжений в спроектированной передаче по формуле

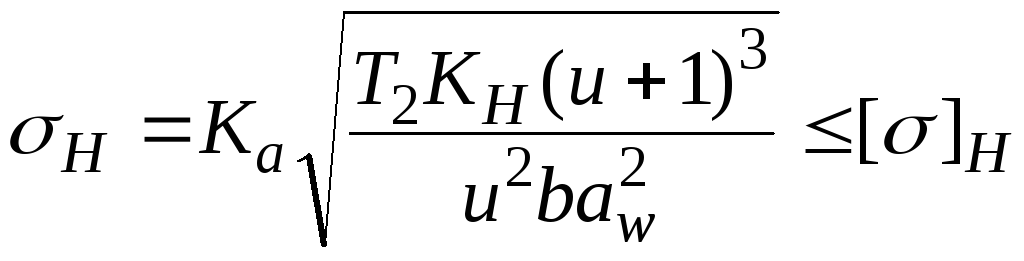. (3.18)

Поскольку в расчетах межцентровое расстояние и модуль передачи округлялись в сторону увеличения, при проверке контактных напряжений достаточно уточнить коэффициент нагрузки , который представляет собой произведение следующих множителей:

. (3.19)

Здесь – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями. Для прямозубых передач принимают . Для косозубых передач 7-ой степени точности и окружных скоростях м/c имеем . При 8-ой степени точности и м/c принимаем .

– коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (b), зависит от расположения колес и коэффициента . При симметричном расположении колес, а также твердости поверхностей зубьев и при имеем . Однако, учитывая дополнительные усилия на вал колеса со стороны ременной передачи, ухудшающие контакт зубьев, рекомендуется принимать увеличенное значение данного коэффициента: .

– динамический коэффициент, зависящий от окружных скоростей. Для прямозубых передач при можно принимать

, для косозубых передач при скоростях м/c этот коэффициент принимают в пределах

Выполнение условия (3.18) после подстановки туда коэффициента гарантирует прочность передачи по контактным напряжениям .