3.2. Модули зубчатых передач. Определение размеров зубчатых колес

Основным параметром, определяющим размеры деталей зубчатых передач, является соответствующий модуль. Для прямозубых колес – это окружной делительный модуль, представляющий собой отношение окружного шага зубьев к числу π (рис. 3.1б):

. (3.2)

Для косозубой передачи определяющим является нормальный модуль: отношение нормального шага зубьев к числу π (рис. 3.2б)

(3.3)

В соответствии с ГОСТ 9563-80, модули зубчатых передач образуют два ряда стандартных значений от 0,1 мм и до 100 мм. Ниже приводятся выдержки их указанного стандарта.

1-.ый ряд (мм)

…0,8…1,0…1,25…1,5…2,0…2,5…3,0…4,0…5,0…6,0…8,0...

2-ой ряд (мм)

…1,375…1,75…2,25…2,75…3,5…4,5…5,5…7,0…9,0…11…

3.2.1. Определение размеров прямозубого колеса

Диаметр делительной окружности прямозубого колеса d можно выразить через окружной делительный модуль, если учесть, что длина делительной окружности , а с другой стороны, , откуда (рис. 3.1б).

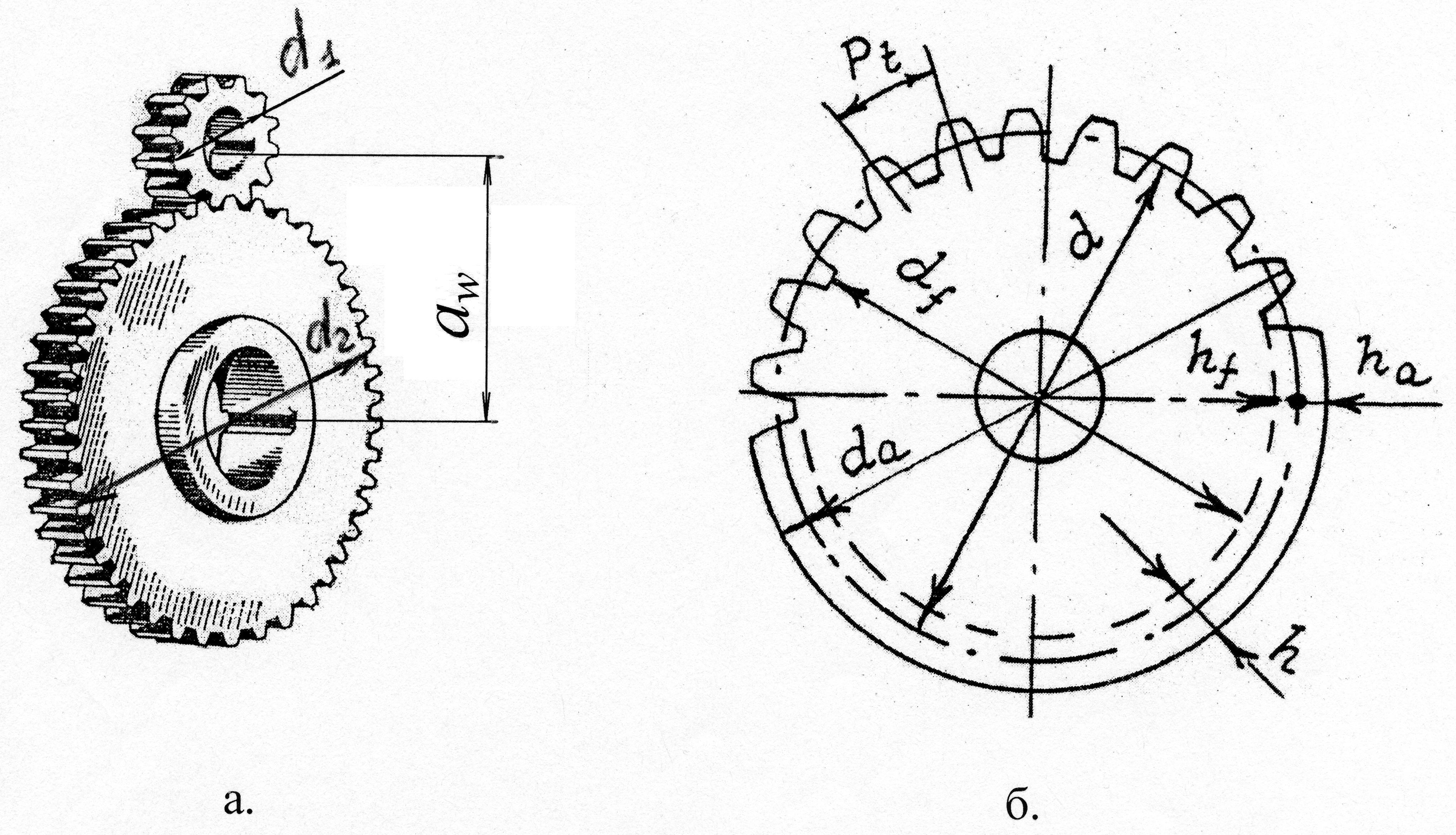
Рис. 3.1

Таким образом, диаметры делительных окружностей шестерни и колеса при числе зубьев и , соответственно, составляют:

, . (3.4)

Учтем при этом, что , где u = u_зп – передаточное число зубчатой передачи. Тогда, как это видно из рис. 3.1а, межцентровое расстояние можно определить выражением:

, (3.5)

Обычно задаются стандартным значением модуля в пределах

m_t = (0,01…0,02)a_w мм, (3.5а)

а затем по формуле (3.5) находят число зубьев шестерни:

; (3.5б)

полученное значение z₁ округляют до целого числа.

Возможно также задаться числом зубьев шестерни в пределах , потом из формулы (3.5) найти модуль передачи, а затем проверить соответствие полученной величины условию (3.5а).

Прочие размеры шестерни и колеса определяют, учитывая , что высота головки зуба принимается равной модулю: , а высота ножки зуба – .Таким образом, имеем:

диаметры окружностей выступов (головок) зубьев :

; (3.6)

диаметры окружностей впадин (ножек) зубьев:

; ; (3.7)

ширина колеса , шестерни – мм; (3.8)

межцентровое расстояние:

Пример 1.3.

Определить размеры колес прямозубой передачи по следующим данным: крутящий момент на колесе: Нм = Нмм, передаточное число (см. пример 1.1). Допускаемое контактное напряжение МПа.

Для расчета прямозубой передачи следует принять . Коэффициент ширины колеса по межцентровому расстоянию пусть будет , а коэффициент нагрузки . Подставляем эти данные в формулу (3.1):

мм.

Окружной делительный модуль должен быть выбран в пределах

мм.

Принимаем мм.

Определяем далее число зубьев малого колеса – шестерни: в соответствии с формулой (3.5б) имеем

.

Число зубьев колеса . Далее определяем параметры зубчатых колес в соответствии с выражениями (3.6)-(3.8):

диаметр делительной окружности шестерни мм;

диаметр окружности выступов: мм;

диаметр окружности впадин: мм;

диаметр делительной окружности колеса: мм;

диаметр окружности выступов: мм;

диаметр окружности впадин: мм.

Межцентровое расстояние: мм.

Длина зуба шестерни (мм), колеса – мм.