
- •Министерство общего и профессионального образования российской федерации санкт-петербургский государственный университет информационных технологий, механики и оптики
- •Введение. Постановка задачи
- •1 Построение и исследование мтч непрерывного оу
- •2 Построение мтч доу и результаты ее исследования
- •3 Синтез закона управления
- •4 Построение матрицы функций модальной чувствительности
- •5 Получение вмо ноу с интервальными параметрами
- •6 Синтез закона медианного модального управления
- •7 Синтез неадаптивного и адаптивного законов управления
- •7.1 Синтез неадаптивного закона управления
- •7.2 Синтез адаптивного закона управления
1 Построение и исследование мтч непрерывного оу
Передаточная функция вход-выход НОУ:
![]()
Перейдем к канонической наблюдаемой форме:
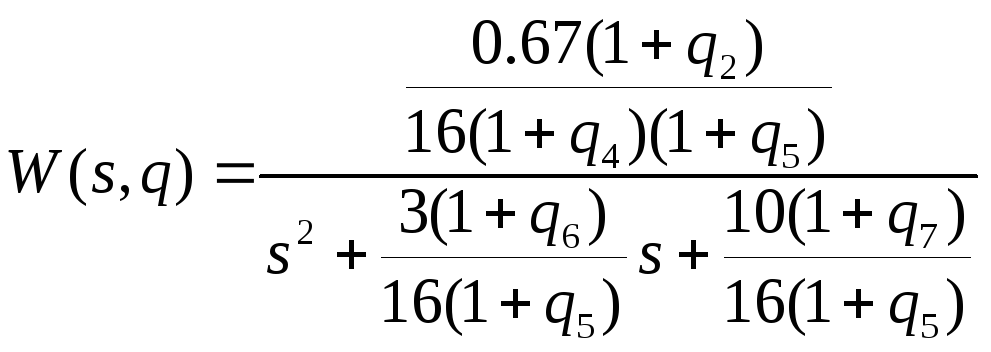
Для перехода к канонической наблюдаемой форме воспользуемся формулами:
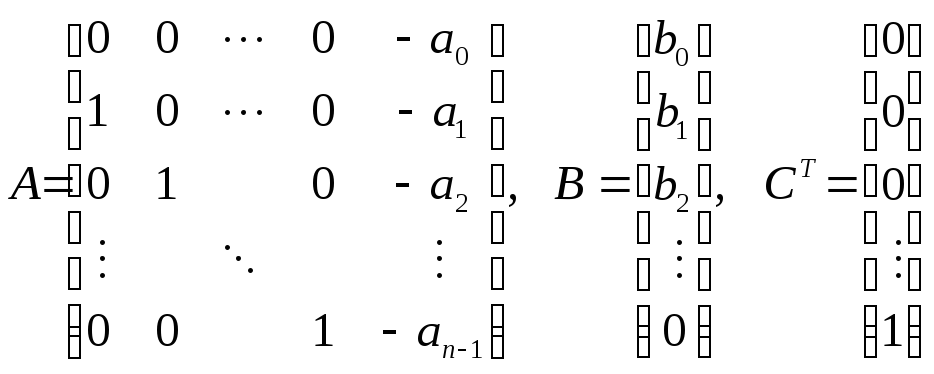
![]() -
представление НОУ:
-
представление НОУ:
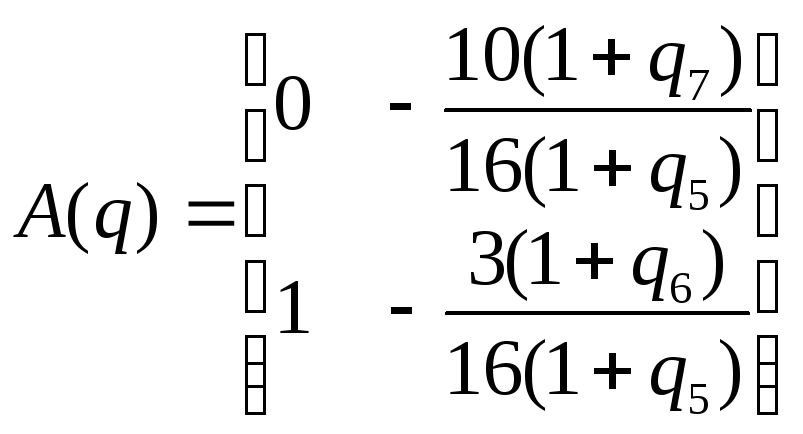 ,
,
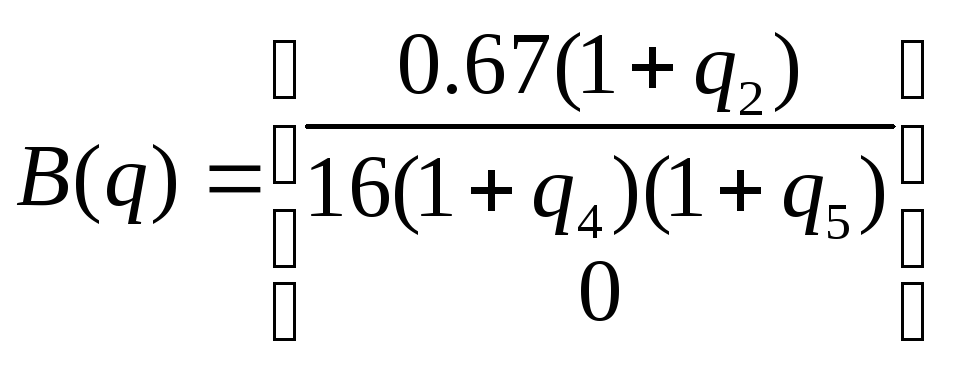 ,
,
![]() .
.
Матрицы номинального ОУ:
![]() ,
,
![]() ,
,
![]() .
.
Построение семейства моделей траекторной чувствительности:
![]()
Где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
и формирование семейства агрегированных систем:
![]()
где
![]() ,
,
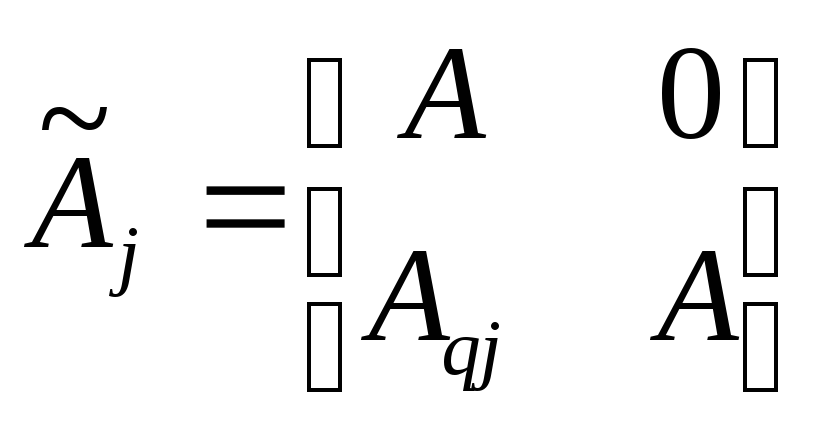 ,
,
![]() ,
,
![]() .
.
Получим:
![]() ,
,
![]() ,
,
 ,
,
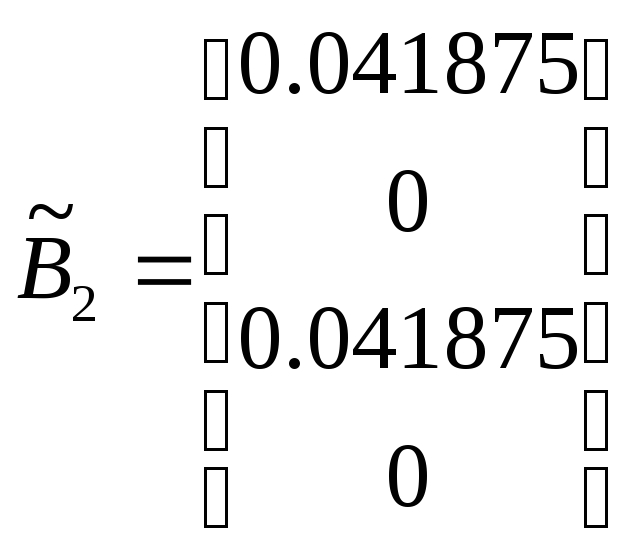 ;
;
![]() ,
,
![]() ,
,
 ,
,
 ;
;
![]() ,
,
![]() ,
,
 ,
,
 ;
;
![]() ,
,
![]() ,
,
 ,
,
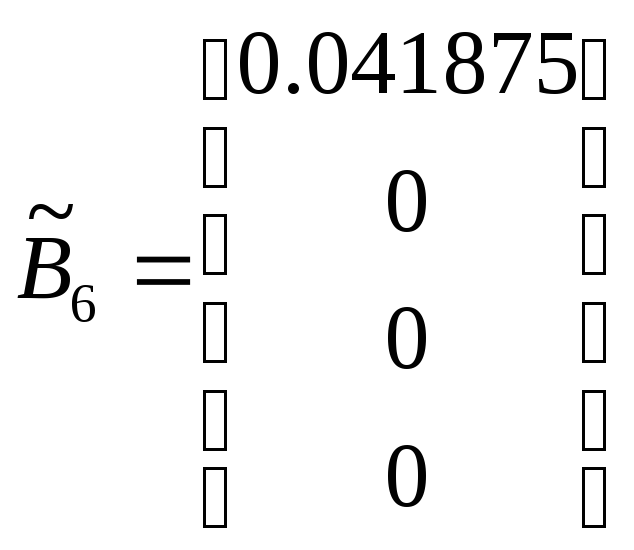 ;
;
![]() ,
,
![]() ,
,
 ,
,
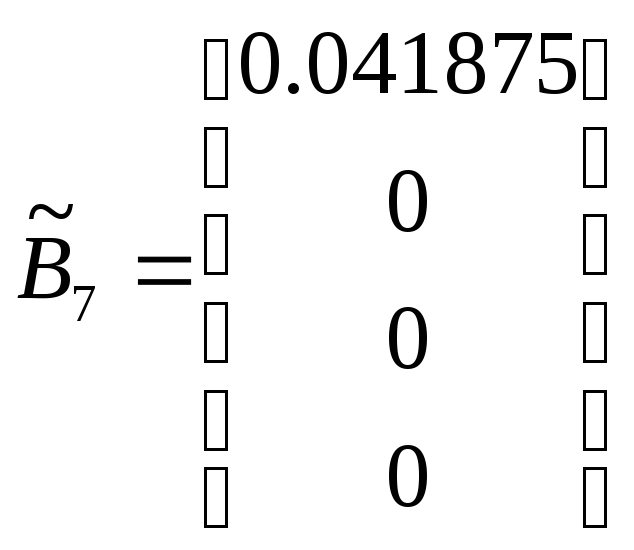 ;
;
Вычислим матрицы управляемости по функции траекторной чувствительности и их абсолютные нормы:
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В силу неравенства:
![]()
проранжируем параметры по потенциальной чувствительности:
![]() .
.
Таким
образом, чем меньше норма соответствующей
матрицы, тем менее чувствительным
является выход по отношению к
соответствующему параметру, и тем
большее управляющее воздействие
потребуется для асимптотической
сходимости к нулю дополнительного
движения, вызванного вариацией
соответствующего параметра. В данном
случае выход ОУ обладает наибольшей
потенциальной чувствительностью по
отношению к параметру
![]() ,
а наименьшей – к параметру
,
а наименьшей – к параметру
![]() .
.
2 Построение мтч доу и результаты ее исследования
Дан
интервал дискретности
![]() и
передаточная функция ОУ:
и
передаточная функция ОУ:
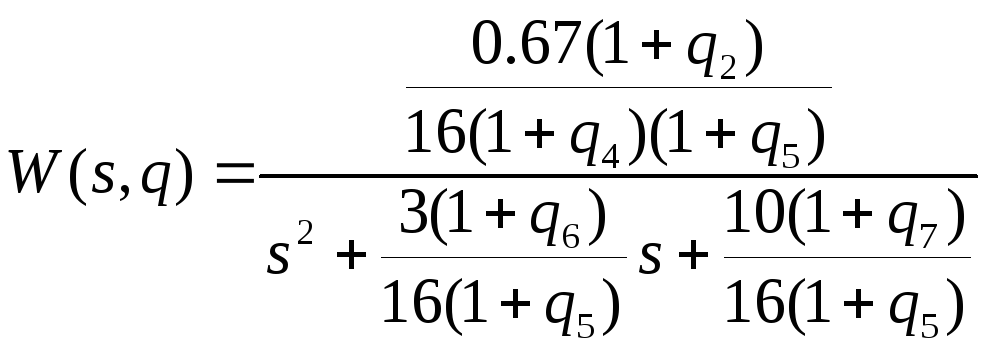
Переход
к дискретному описанию ОУ осуществляется
методом замены переменной разностью
конечных малых. Так
как строится МТЧ к вариации интервала
дискретности, то будем использовать
формулы, представляя
![]() как
как
![]() ,
где
,
где
![]() .
.
Заменим производную вектора состояния разностью конечных малых:
![]()
тогда
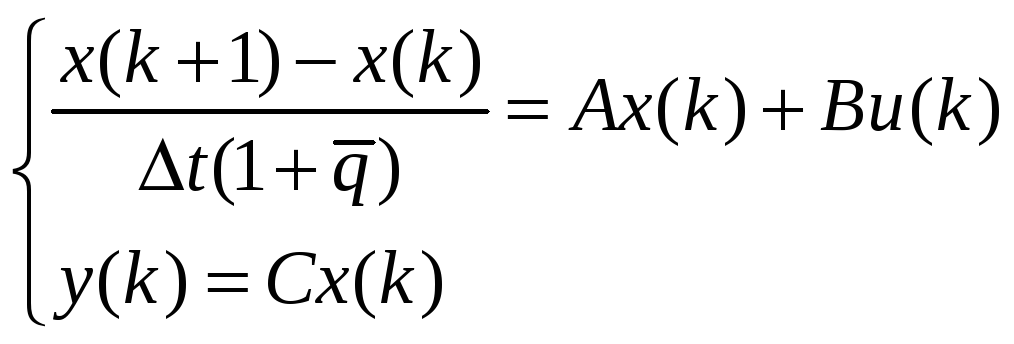
![]()
![]()
![]()
Таким образом, переход к дискретному описанию осуществляется по формулам:
![]()
Матрицы ДОУ модели «Вход-Состояние-Выход» примут вид:
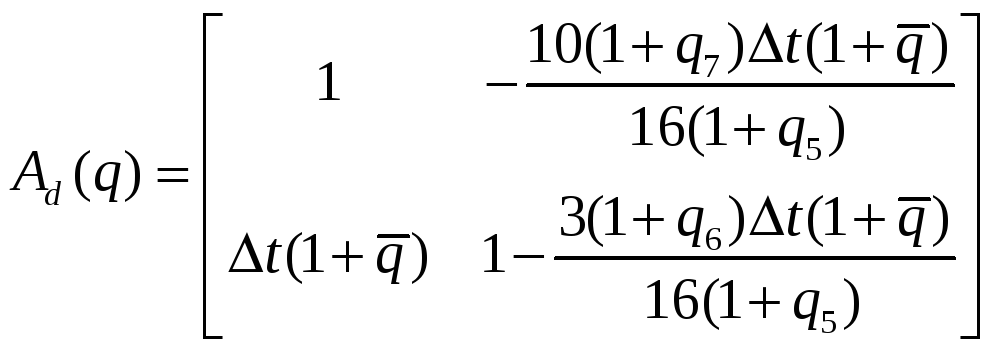 ,
,
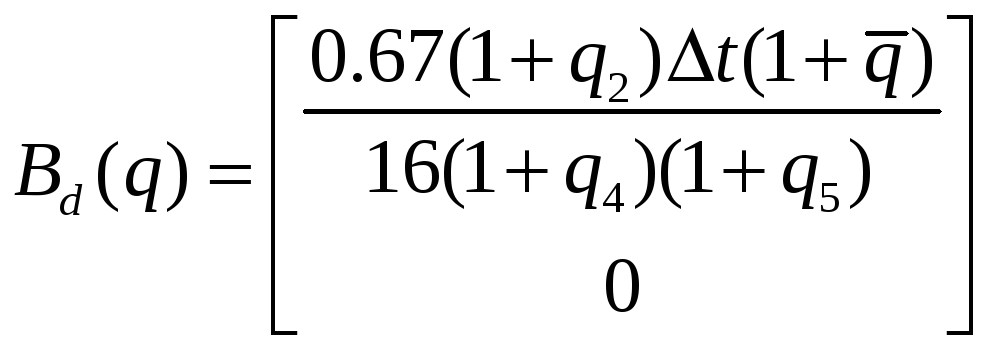 ,
,
![]() .
.
Таким образом матрицы номинального дискретного ОУ примут вид:
![]() .
.
Построим модель траекторной чувствительности к вариации интервала дискретности:
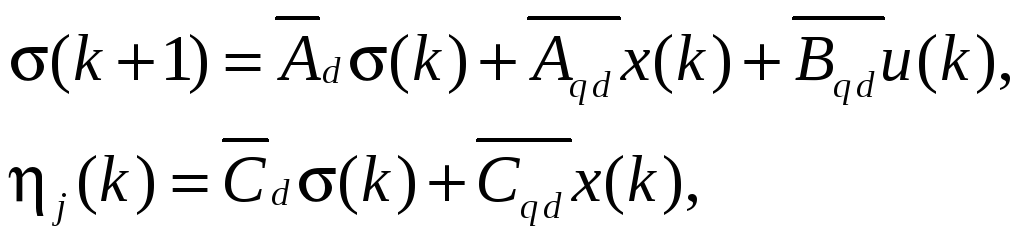
где 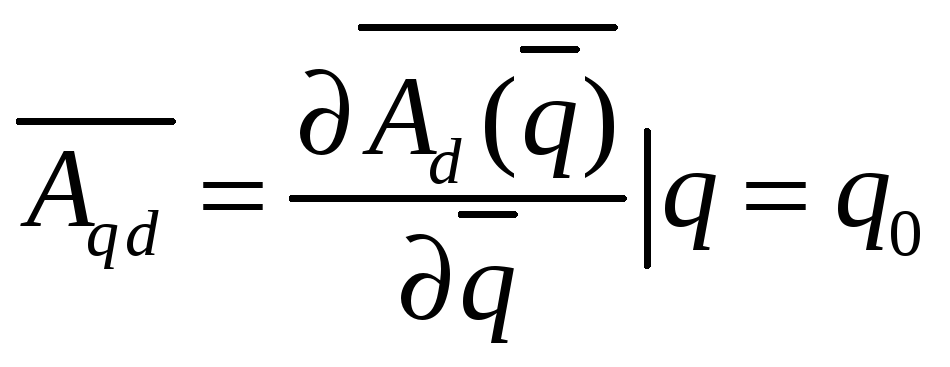 ,
,
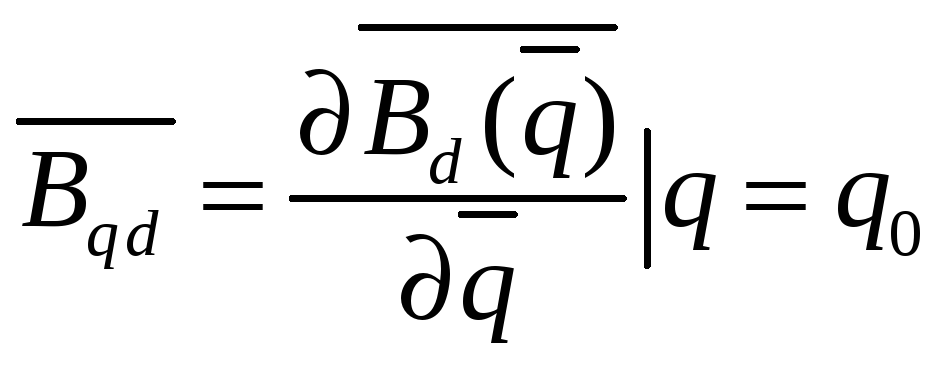 ,
,
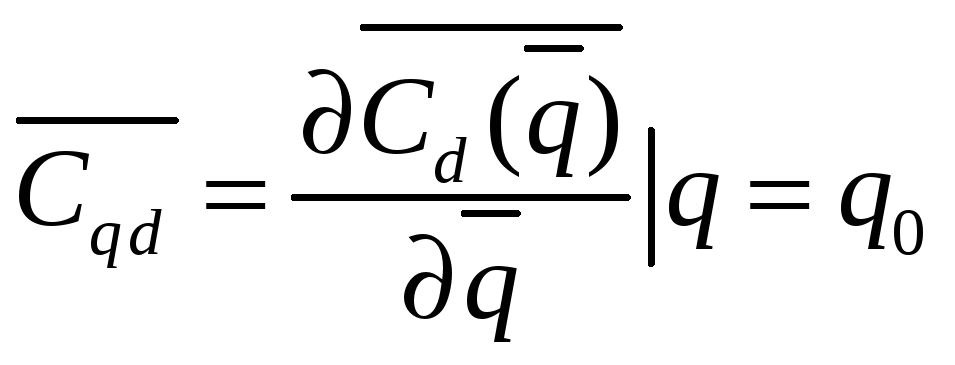 ,
,
![]() ,
,
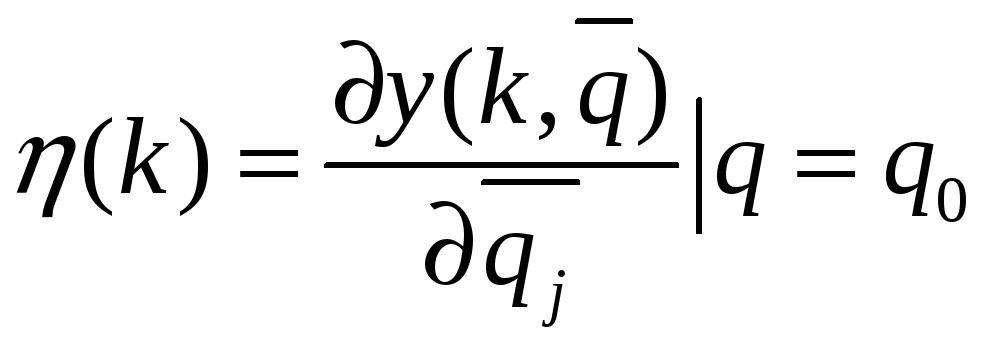 ,
,
При
условии, что qj=0,
j=(1,p),
![]() – вариация интервала дискретности:
– вариация интервала дискретности:
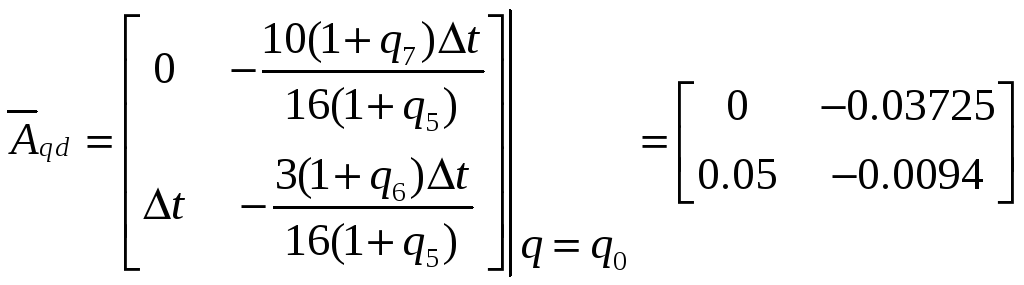

![]() .
.
Построим агрегированный ОУ:
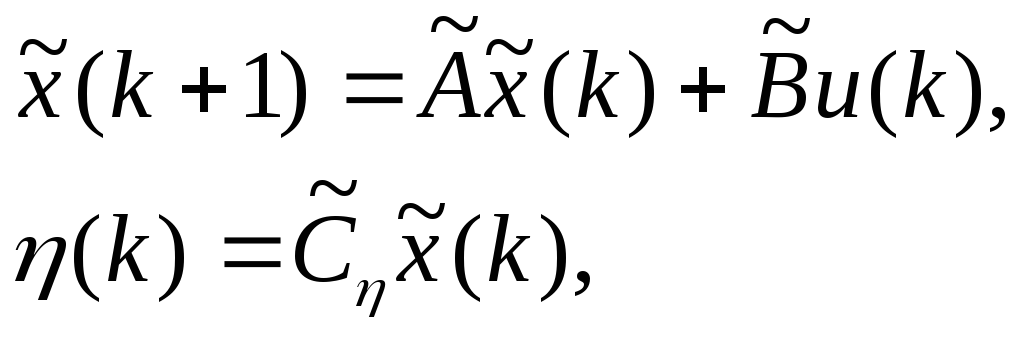
где
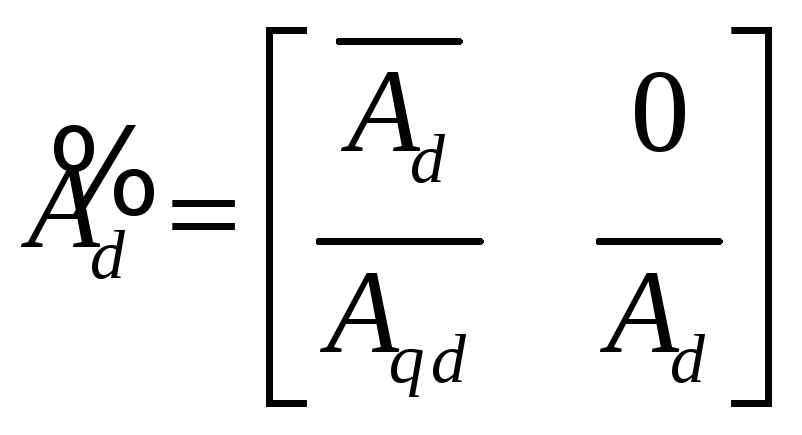 ,
,
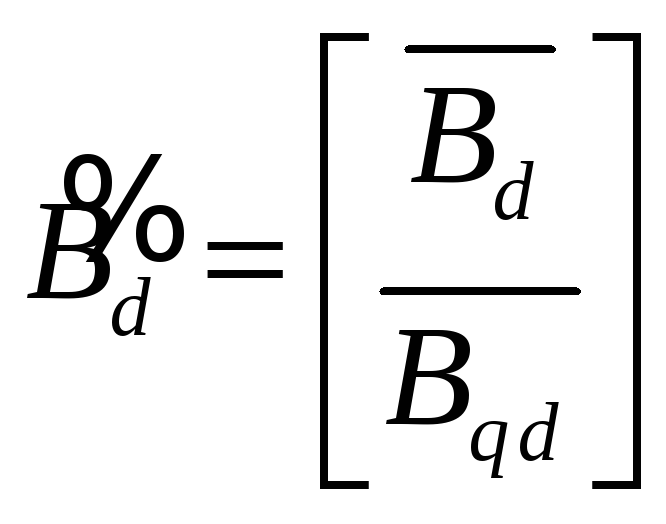 ,
,
![]() .
.
Получим:
 ,
,
 ,
,
![]()
3 Синтез закона управления
Как было показано в пункте 1, ОУ имеет вид:
![]() ,
,
где
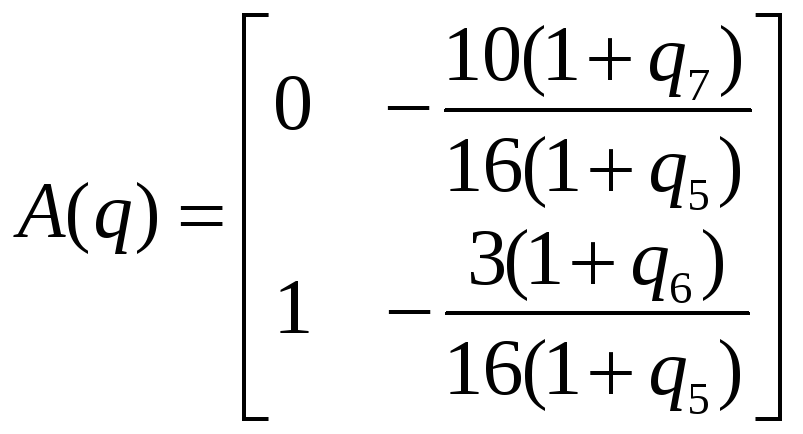 ,
,
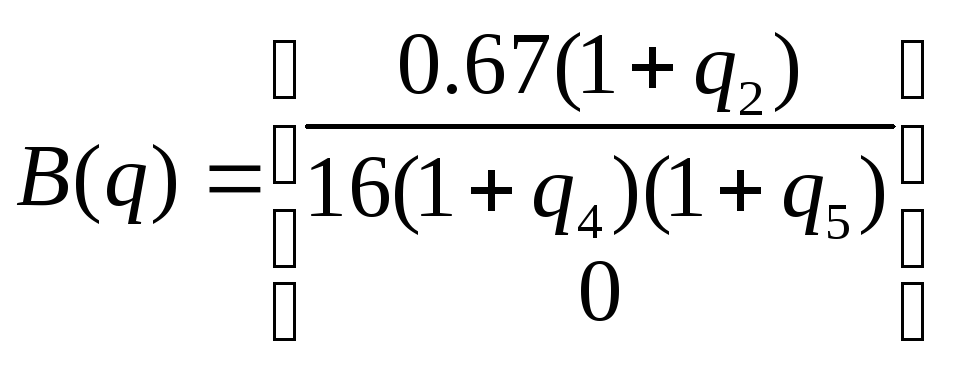 ,
,
![]() .
.
Закон
управления (ЗУ):
![]() должен доставлять замкнутой системе
должен доставлять замкнутой системе
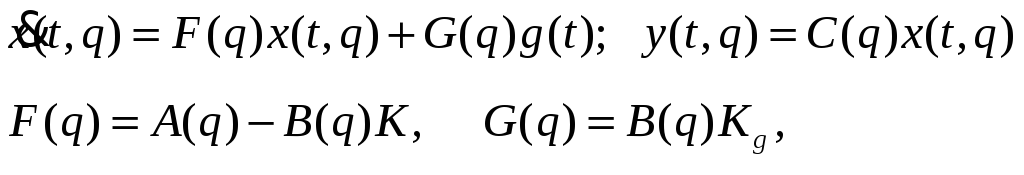
образованной объединением НОУ и ЗУ, равенство входа g(t) и выхода y(t) в неподвижном состоянии при номинальных значениях параметров с помощью:
- матрицы kg прямой связи по входу g(t);
- матрицы k обратной связи по состоянию x(t)
распределение
мод Баттерворта с характеристической
частотой
![]() .
.
Выберем желаемый полином Баттерворта следующим образом:
![]()
Желаемые
корни:
![]()
Выберем эталонную модель:
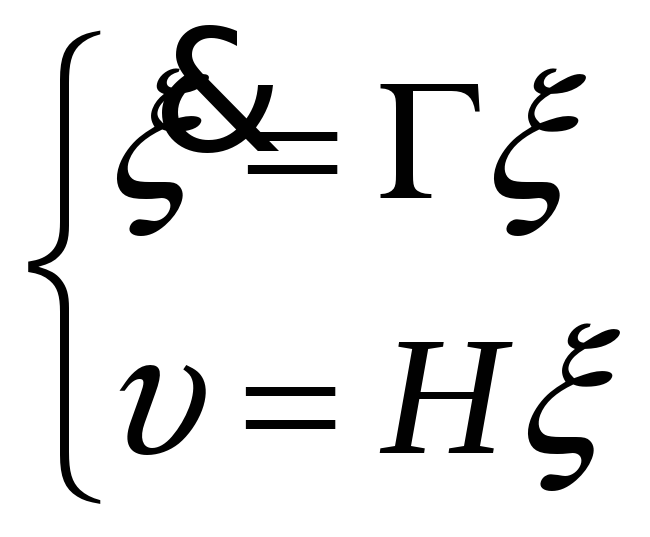 ,
,
где матрицы Г и Н выбираются из условия полной наблюдаемости пары Н,Г, например, следующим образом:
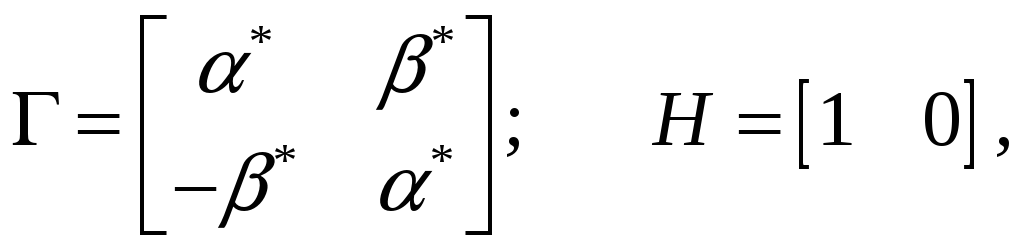
где
![]() - комплексно-сопряженные корни желаемого
характеристического полинома.
- комплексно-сопряженные корни желаемого
характеристического полинома.
![]()
Пусть
вектора
![]() и
и
![]() связаны матрицей преобразования М:
связаны матрицей преобразования М:
![]()
Матрицы М и K находятся из следующих соотношений:
![]()
Решая уравнение Сильвестра для номинальных значений, получаем матрицу М и затем матрицу ЛСОС К:
![]()
Найдем
![]() :
:
![]()
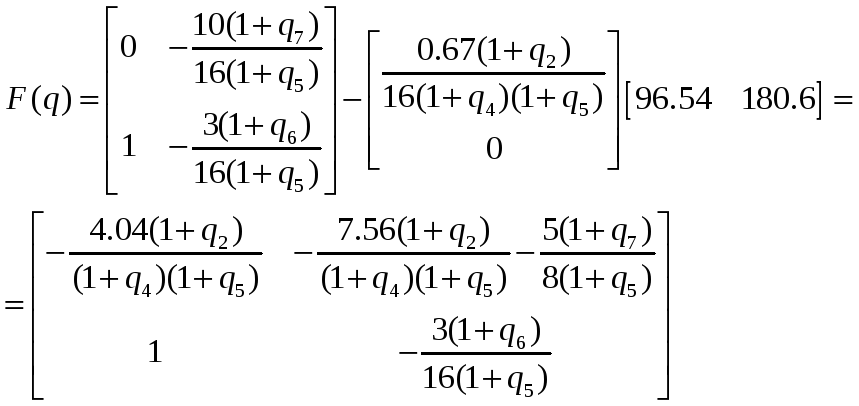
Найдем
![]() :
:
![]() ,
, 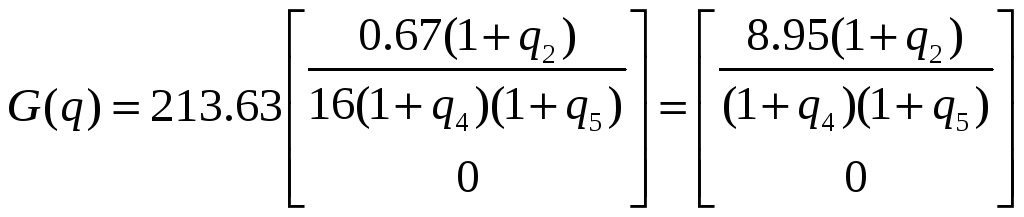
Значение матриц F и G при номинальных параметрах:
![]() ;
;
![]()
![]() находится
из условия равенства входа g(t)
и выхода
y(t)
в неподвижном
состоянии.
находится
из условия равенства входа g(t)
и выхода
y(t)
в неподвижном
состоянии.
![]()
Математическая версия закона управления:
![]() ,
,
Реализационная версия имеет вид:
![]()
![]()
Передаточная функция замкнутой системы:
![]()
Схема моделирования замкнутой системы представлена на рисунке 1, переходная функция – на рисунке 2.
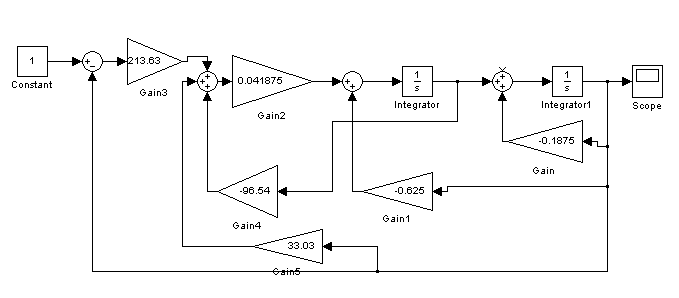
Рисунок 1 – Схема моделирования замкнутой системы

Рисунок 2 – Переходная функция замкнутой системы
Построим семейство моделей траекторной чувствительности:
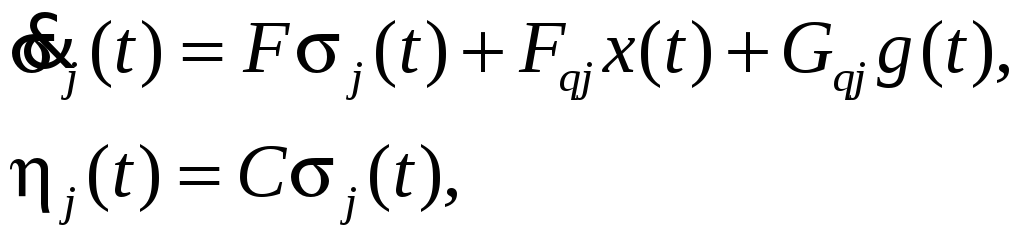
где
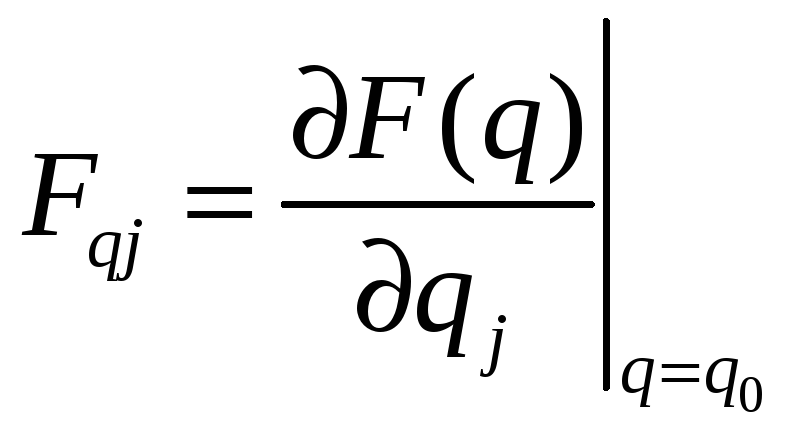 ,
,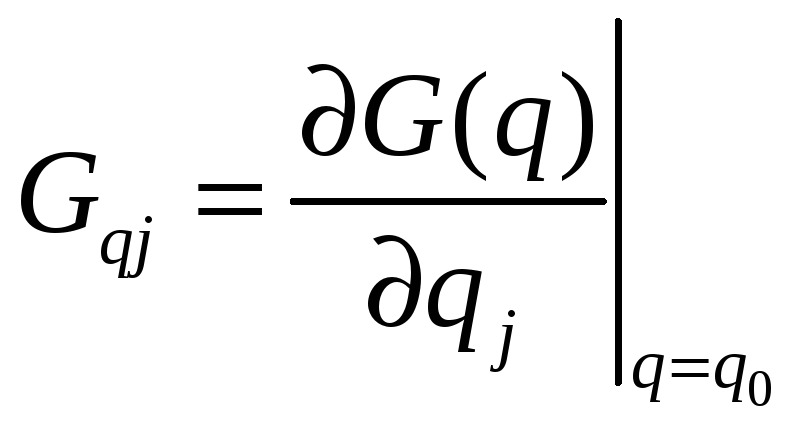 ,
,
 ,
,
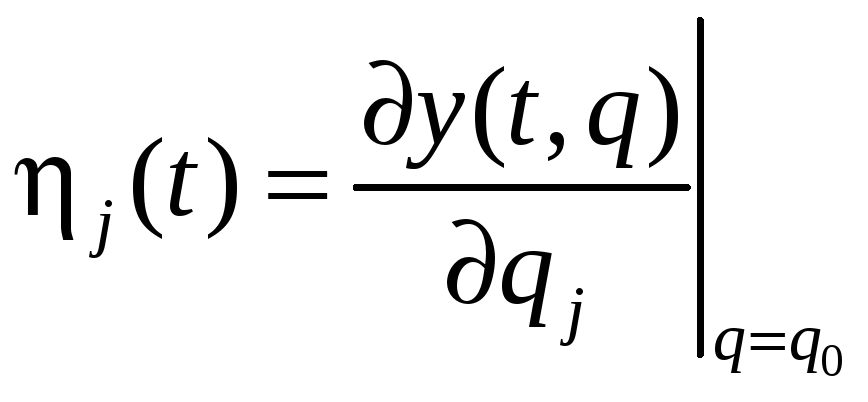 .
.
И сформируем семейство агрегированных систем:

где
![]() ,
,
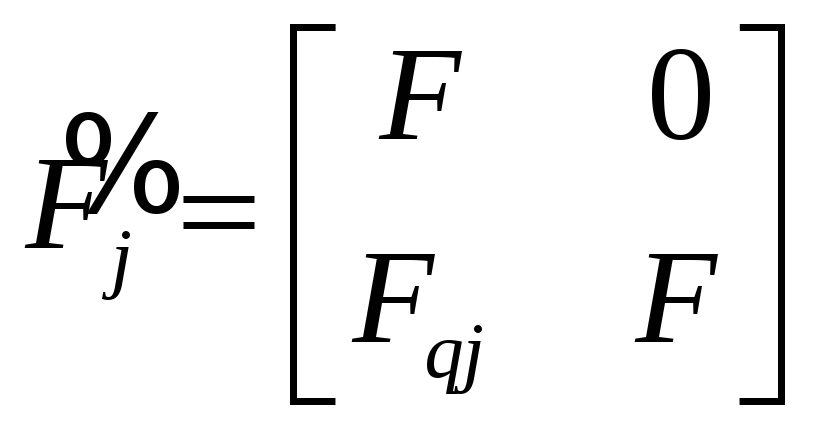 ,
,
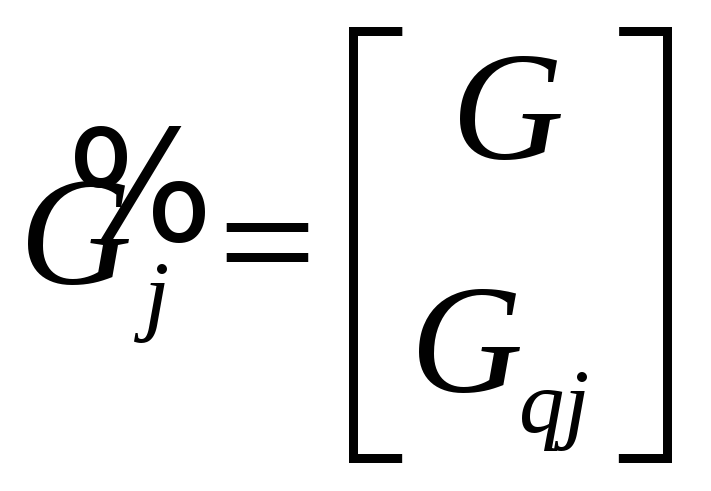 ,
,
![]() .
.
Получим:
![]() ,
,
![]() ,
,
 ,
,
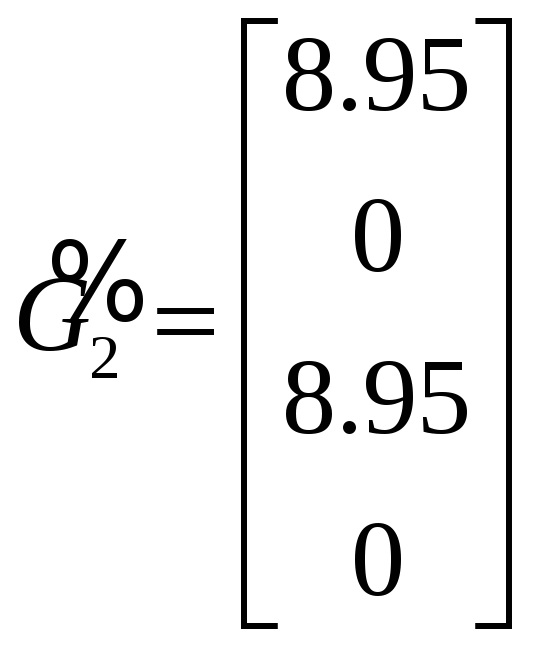 .
.
![]() ,
,
![]() ,
,
 ,
,
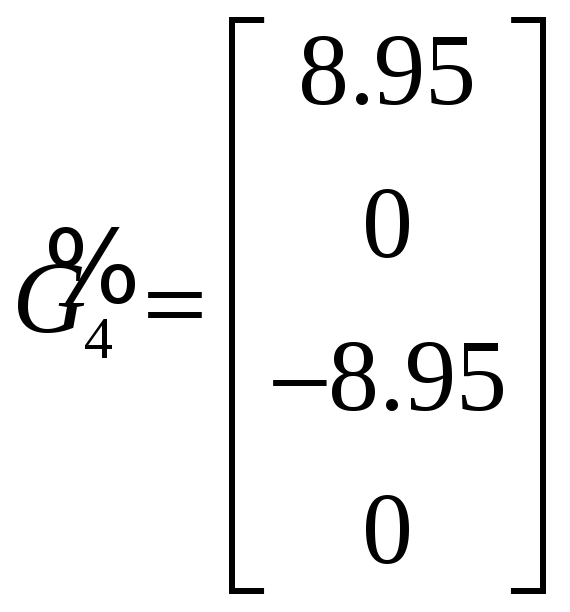 .
.
![]() ,
,
![]() ,
,
 ,
,
 .
.
![]() ,
,
![]() ,
,
 ,
,
 .
.
![]() ,
,
![]() ,
,
 ,
,
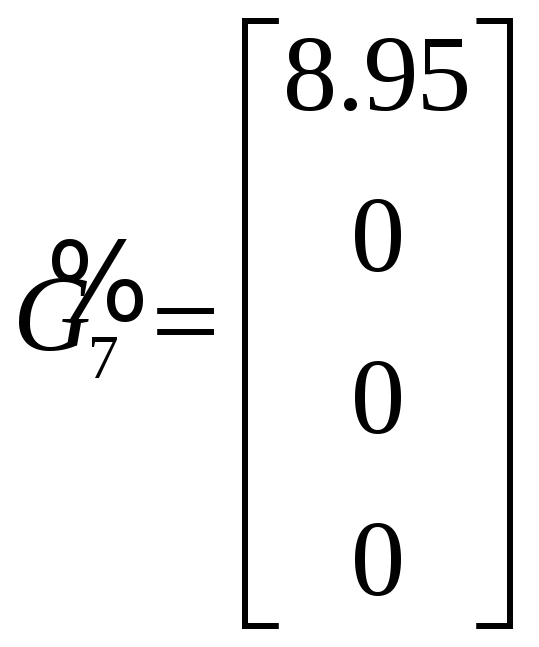 .
.
Схема моделирования агрегированной системы (номинального объекта управления и модели траекторной чувствительности к вариации одного из параметров) приведена на рисунке 3.
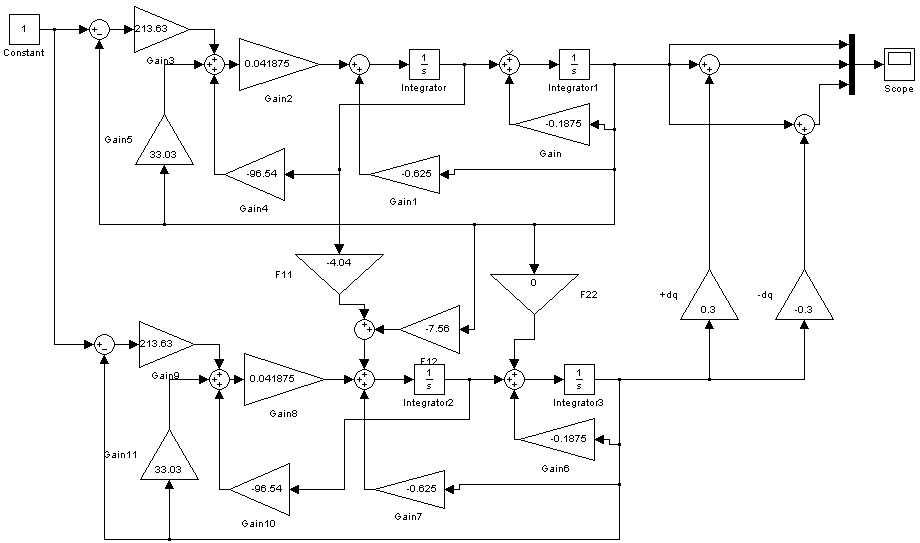
Рисунок 3 – Схема моделирования агрегированной системы
Результаты моделирования номинальной системы и параметрически возмущенной по каждому из параметров представлены на рисунках 4-8.


Рисунок
4 – Переходные функции агрегированной
системы при
Рисунок
5 – Переходные функции агрегированной
системы при
![]()
![]()
Рисунок
6 – Переходные функции агрегированной
системы при
Рисунок
7 – Переходные функции агрегированной
системы при
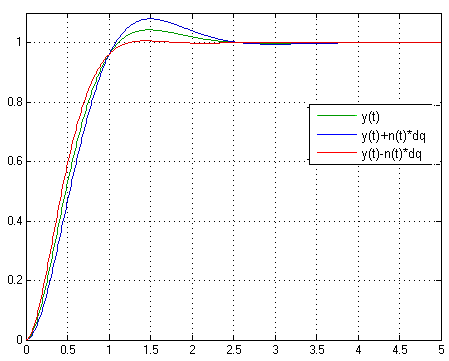
![]()
![]()

Рисунок
8 – Переходные функции агрегированной
системы при
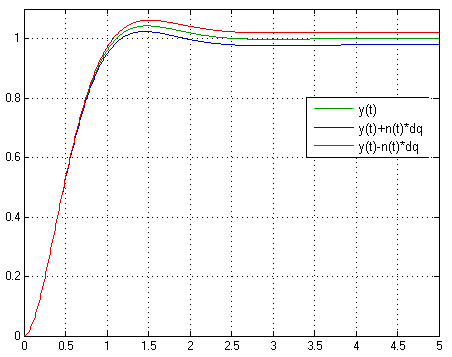
![]()
Влияние вариаций параметров на показатели качества системы отражено в таблице 1.
Таблица 1 - Влияние вариаций параметров на показатели качества системы
|
Варьируемый параметр |
|
|
|
|
|
- |
0,98 |
4,3 |
0 |
0 |
|
|
1,928 |
8,4 |
96,7 |
95,3 |
|
|
1,928 |
8,4 |
96,7 |
95,3 |
|
|
1,904 |
8 |
94,3 |
86 |
|
|
0,988 |
4,4 |
0,82 |
2,3 |
|
|
1 |
4,6 |
2,04 |
7 |
Таким образом, параметры по степени влияния на качество процессов следует проранжировать следующим образом:
![]() .
.
