Обработка результатов косвенных измерений

1. Косвенными являются измерения, при которых искомую физическую величину Z определяют путем вычислений по результатам прямых измерений других величин. Поэтому после проведения прямых измерений и оценки их неопределенностей (погрешностей) необходимо вычислить среднее значение искомой величины (Z_ср) по рабочей формуле, в которую подставляют средние значения величин, полученных из прямых измерений.

2. Для оценки неопределенностей (погрешностей) косвенных измерений ве­­личины Z необходимо вывести формулу для ее относительной погрешности . Пусть искомая величина Z является функцией нескольких переменных: .

Тогда

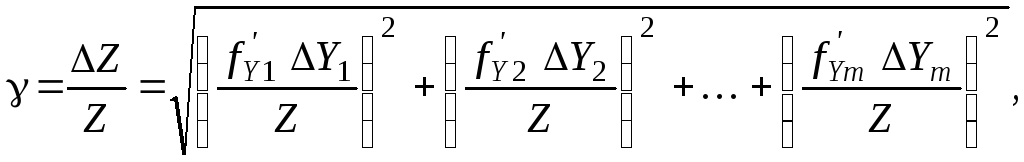(7)

где – частные производные, которые вычисляются при средних значениях результатов прямых измерений Y_m; Y_m – граница доверительного интервала для прямого измерения Y_m.

Формула для расчета относительной неопределенности косвенных измерений в некоторых простейших случаях представлена в таблице 2, где символы Y обозначают границы доверительного интервала для измеряемых величин Y.

Таблица 2

Вид функциональной зависимости	Относительная стандартная неопределенность
Z = Y1  Y2
Z = Y1 Y2
Z = Y1 / Y2

3. После вывода формулы относительной погрешности необходимо по ней вычислить значение , а затем определить доверительный интервал Z искомой величины:

Z = Z_ср ^. 

Окончательный результат следует представить в стандартной форме:

(Z_ср – Z) … (Z_ср + Z).

Работа 60: резонанс в электрическом колебательном контуре

1. Цель работы

Ознакомление с электрическим колебательным контуром (на примере последовательного контура) и явлением резонанса в контуре. Экспериментальное определение индуктивности контура.

2. Основные теоретические положения

Наряду с механическими колебаниями и колебательными системами существуют электрические, точнее электромагнитные, колебания и колебательные системы. Такие колебательные системы являются непременной частью многих радиоприемных и передающих устройств.

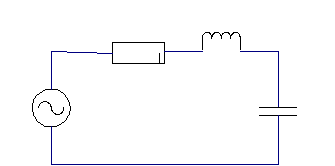
Рис. 1

Простейшей электрической колебательной системой является так называемый последовательный колебательный контур, состоящий из последовательно подключенного резистора R, катушки индуктивности L и конденсатора С (рис.1).

Если такой контур присоединить к источнику переменной ЭДС (), то в таком контуре устанавливаются вынужденные гармонические колебания, совершающиеся с частотой ω источника.

Согласно второму правилу Кирхгофа, действующая в контуре ЭДС равна сумме падений напряжений на его элементах:

(1)

где – соответственно падения напряжения на резисторе, катушке индуктивности и конденсаторе.

Падения напряжения соответственно равны

(2)

где q – заряд на обкладках конденсатора, – ток в контуре.

Подставив в (1) выражения для , и из (2), получим

(3)

Продифференцируем это выражение по времени

.

Подставив в это выражение, найдем дифференциальное уравнение вынужденных колебаний, которому должна удовлетворять сила тока в контуре: (1)

(4)

Частное решение этого уравнения будем искать в виде периодической функции от времени:

(5)

где I₀ – амплитуда тока, а φ – разность фаз между током и ЭДС. Составляя первую и вторую производные от тока I по времени, получим:

Из полученных соотношений видно, что напряжения на конденсаторе и катушке индуктивности сдвинуты по фазе на 180⁰, т.е. противофазны.

Подставляя значения и I в уравнение (4) и разделив правую и левую части на ω, найдем:

Представляя и через синусы и косинусы от ωt и φ, получим:

Так как это равенство должно выполняться для любого момента времени, то множители при и должны равняться нулю, откуда получаем два уравнения:

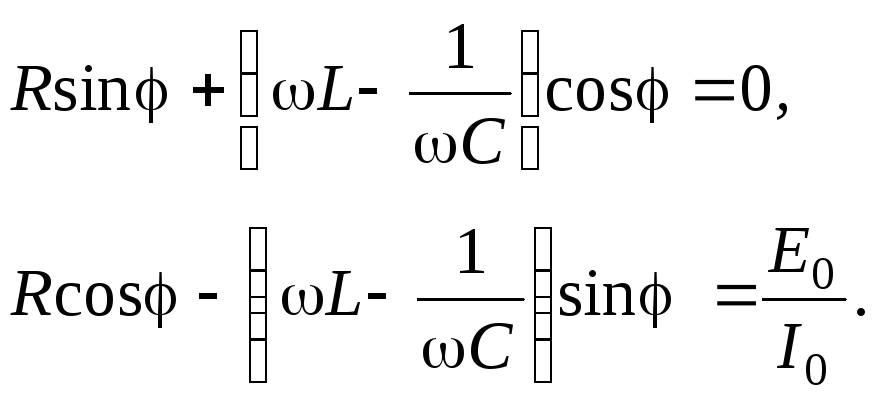(6)

Из первого уравнения (6) имеем:

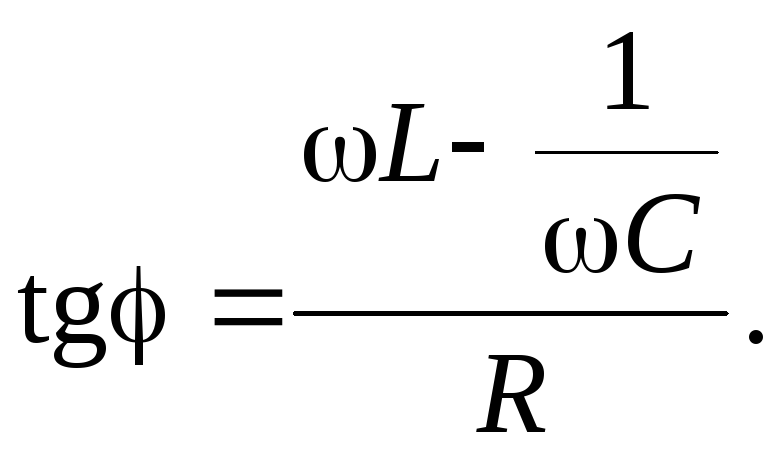(7)

Возводя равенства (6) в квадрат и складывая их, найдем:

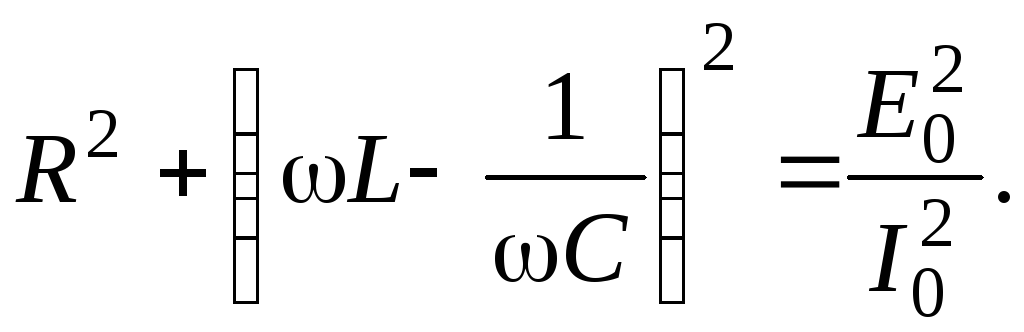
Таким образом, амплитуда тока в контуре равна

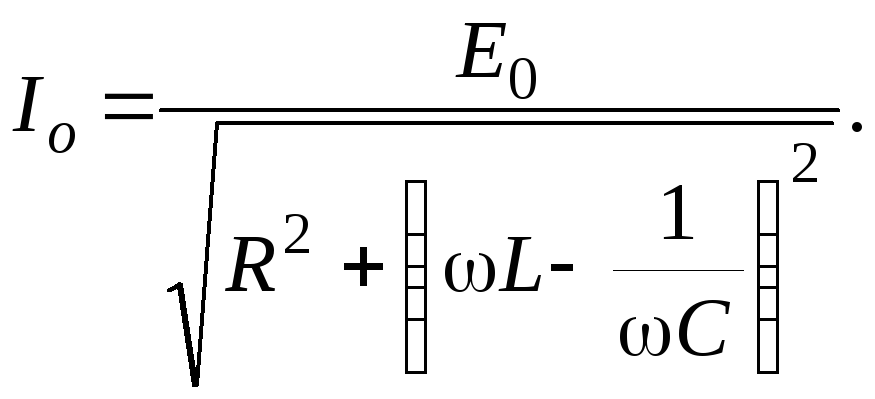(8)

Равенства (5), (7) и (8) дают искомое решение: в цепи течет ток I того же периода, что и приложенная ЭДС; амплитуда этого тока I₀ определяется равенством (8). Ток сдвинут по фазе относительно ЭДС на угол φ, определяемый равенством (7).

Величина называется полным сопротивлением цепи, которое зависит как от значений R, L, C, так и от частоты тока ω, и состоит из активного (омического) R и полного реактивного сопротивлений . Таким образом, , где , – индуктивное, – емкостное реактивные сопротивления. При некоторой частоте ω = ω_рез, называемой резонансной частотой, полное реактивное сопротивление обращается в нуль:

(9)

а полное сопротивление достигает минимума и равно омическому сопротивлению Z = R; на этой частоте амплитуды падений напряжений на катушке индуктивности и на конденсаторе равны, а амплитуда силы тока достигает максимального значения:

Это явление носит название резонанса: амплитуда силы тока достигает максимума при некотором определенном значении частоты , которое совпадает с собственной частотой ω₀ контура для незатухающих колебаний и значение которой в соответствии с формулой (9), равно:

. (10)

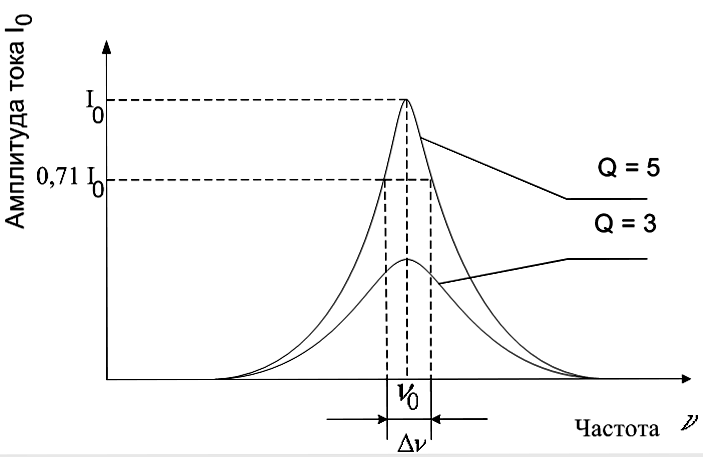
Зависимость от частоты амплитуды тока I₀ , а также напряжений U_0L и U_0C называют резонансными кривыми и имеют тем более острый максимум, чем меньше омическое сопротивлений R (рис.2 а,б):

а)

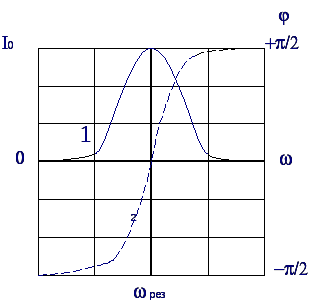
б)

Рис. 2

Так как ток в цепи максимален, то на резонансной частоте падения напряжений на конденсаторе и катушке индуктивности достигают больших и одинаковых по амплитуде значений:

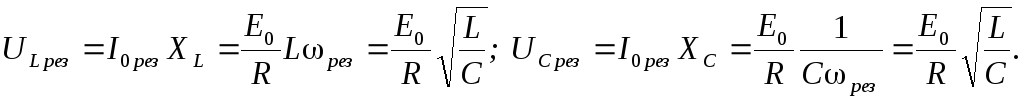(11)

Величина называется волновым сопротивлением контура.

По формуле (7) при резонансе разность фаз φ = 0. При разность фаз , т.е. ток опережает значение ЭДС; при разность фаз ; в этом случае ток отстает от ЭДС. На рис. 2а кривая 1 дает изменение силы тока с частотой при заданной ЭДС и постоянных L и C; кривая 2б дает зависимость сдвига фазы φ от частоты.

Соотношения между переменным током I и напряжениями делаются особенно наглядными, если изображать их (как и гармонические колебания) с помощью векторов. Выберем произвольное, предпочтительнее горизонтальное, направление, которое назовем осью токов (рис.3).

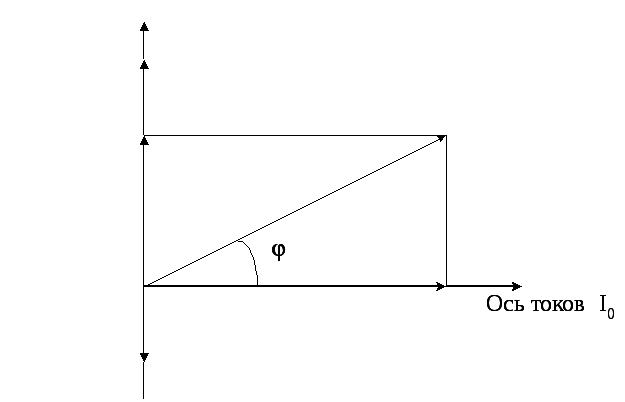
Рис. 3

Отложим вдоль этого направления вектор тока длиной I₀. Посмотрим, как соотносятся вектора по отношению друг к другу и вектору тока I₀:

а) вектор U_R = R I = совпадает по направлению с вектором тока I. Отложим U_0R вдоль вектора тока.

b) вектор ; т.е. напряжение U_L опережает ток I на π/2. Отложим U_0L вертикально вверх.

c) вектор ; т.е. напряжение U_C отстает от тока I на π/2. Отложим U_0C вертикально вниз.

Из рис.3 видно, что, как ранее было отмечено, вектора U_L и U_C направлены противоположно по отношению друг к другу. На резонансной частоте падение напряжения на катушке индуктивности и конденсаторе, согласно (9), равны. На резонансной частоте напряжения на катушке индуктивности и на конденсаторе компенсируют друг друга и ЭДС становится равной U_R. Поэтому явление резонанса в последовательном контуре называется резонансом напряжений.

Вне резонанса реактивное сопротивление контура уже не равно нулю, полное сопротивление Z возрастает, а амплитуда тока уменьшается по сравнению со значениями на резонансе.

Качество колебательного контура характеризуется добротностью, которая обычно значительно больше единицы и равна отношению запасенной в контуре энергии за один период к теряемой контуром энергии (выделение тепла на омическом сопротивлении) за тот же период, и может быть определена как

(12)

Из выражений (11) видно, что на резонансе , следовательно,

добротность показывает, во сколько раз на резонансе амплитуда напряжения на конденсаторе (или на катушке индуктивности) больше амплитуды ЭДС.

Добротность характеризует остроту резонансных кривых и может быть непосредственно определена экспериментально. В случае малых значений затуханий (потерь) добротность определяется соотношением:

(13)

где , где и – частоты, на которых амплитуда тока в раз меньше резонансного значения. Добротность Q и логарифмический декремент колебаний λ контура связаны соотношением: