4. Определение оптимальной стратегии производства в условиях неопределенности цен на ресурсы и готовую продукцию

При каждом i-м уровне цен решая задачу линейного программирования

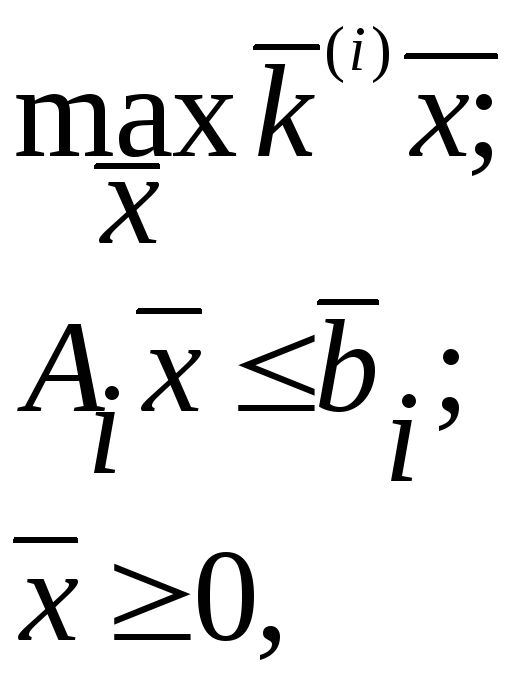
мы получили соответствующие оптимальные программы выпуска изделий , обеспечивающие максимальные прибыли при каждом i-м состоянии «внешней среды»:

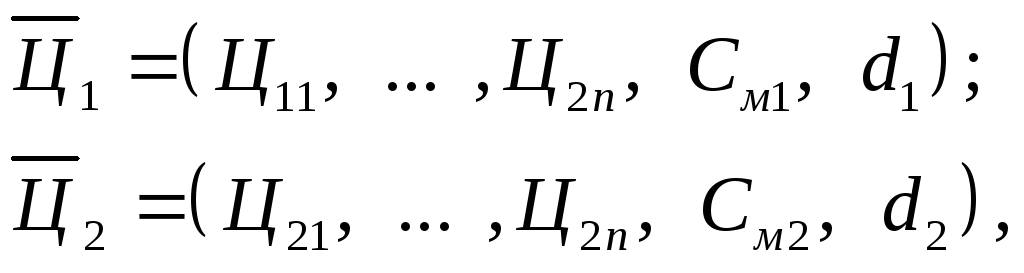
которым соответствуют две оптимальные стратегии выпуска продукции:

обеспечивающие в каждом отдельном случае максимальную прибыль:

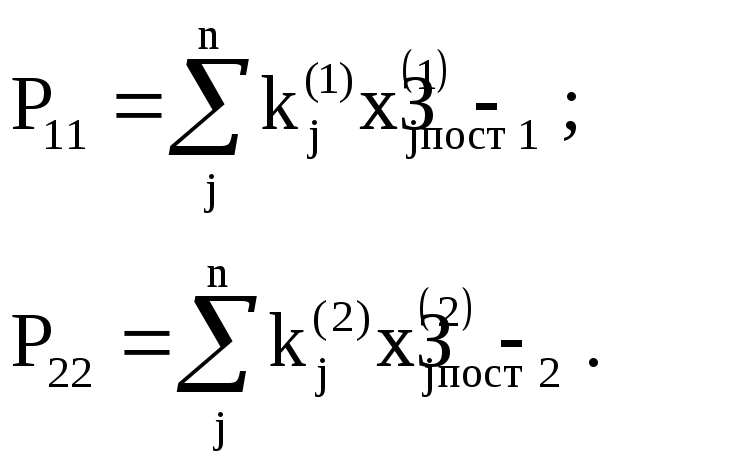
Ставится задача: определить оптимальную стратегию выпуска продукции, обеспечивающую максимальную гарантированную прибыль в условиях неопределенности состояния «внешней среды».

4.1. Построение матричной игры с «внешней средой»

Сформулированная задача может быть разрешена с помощью теории матричных (стратегических) игр, для чего необходимо составить матрицу возможных прибылей

,

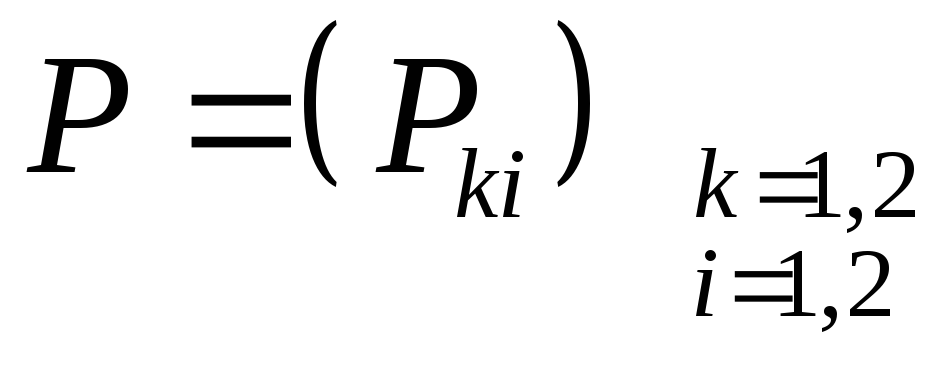которая представлена в виде табл. 4.

Таблица 1

Матрица возможных прибылей

Уровень цен i Программа выпуска k

Из матрицы возможных прибылей следует:

1. Если будет реализована чистая стратегия производства , то в зависимости от состояния «внешней среды» прибыль предприятия составит либо при уровне цен , либо при уровне цен .

Прибыль

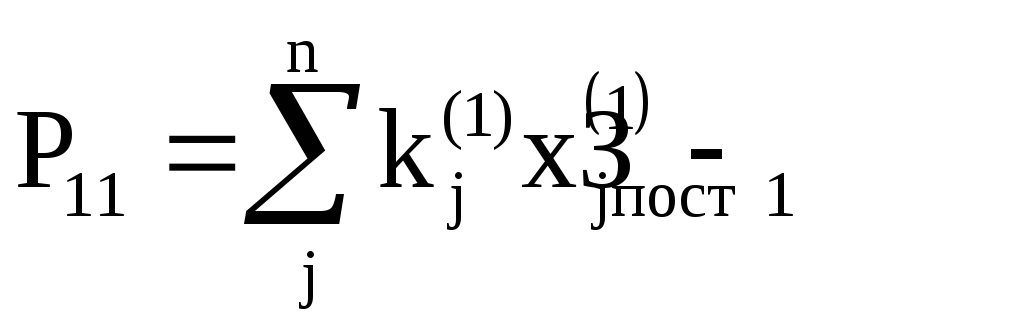
определяют решением задачи

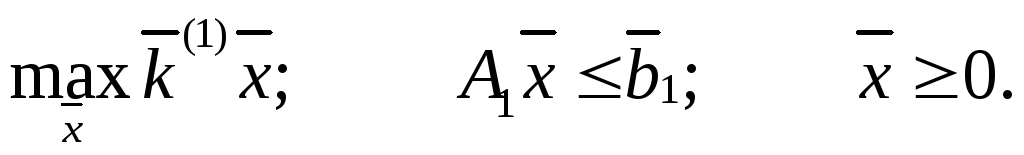
При этом трудоемкость годовой программы выпуска продукции равна

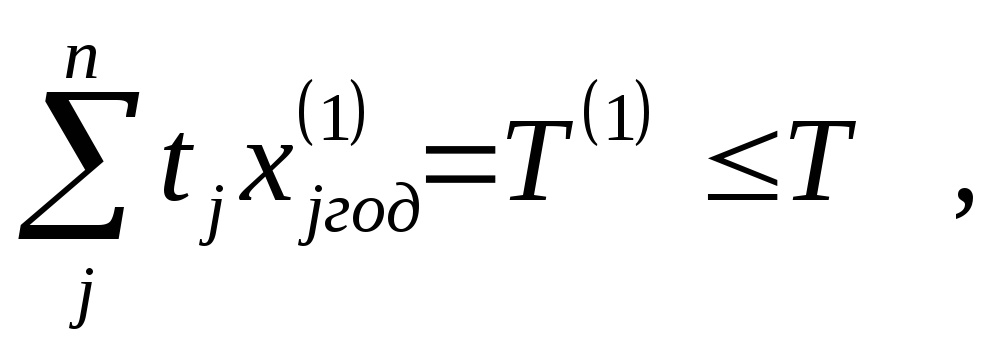
а производственные затраты составляют

Прибыль определяется как

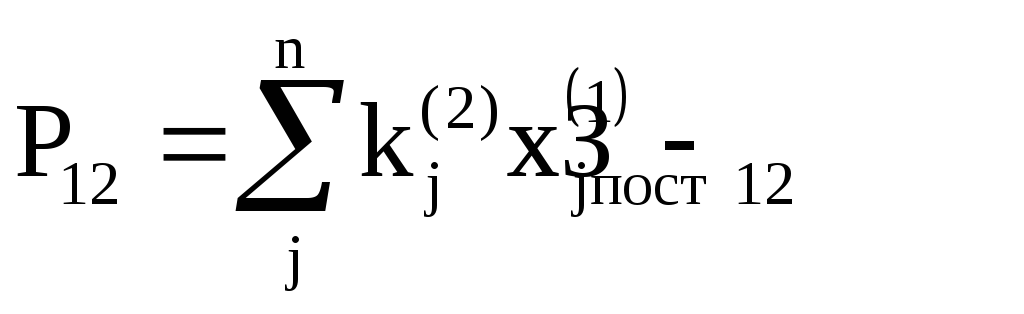
при условии, что производственные затраты не превышают расчетную величину :

Если же ограничения по производственным затратам не выполняются, то прибыль рассчитывают по формуле

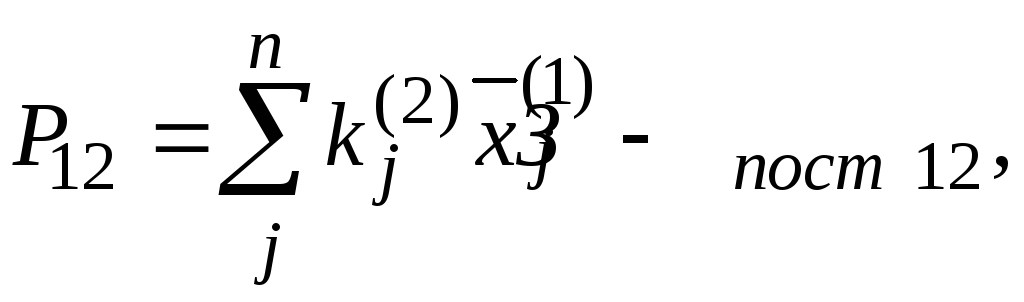
где

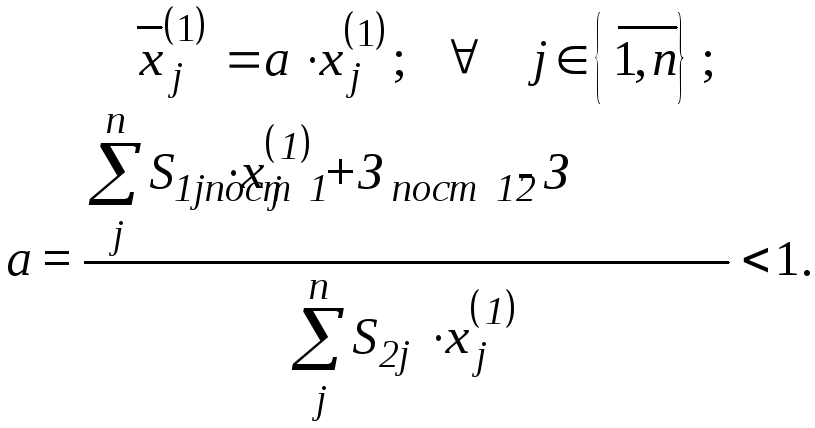
В этом случае трудоемкость годовой программы выпуска продукции равна

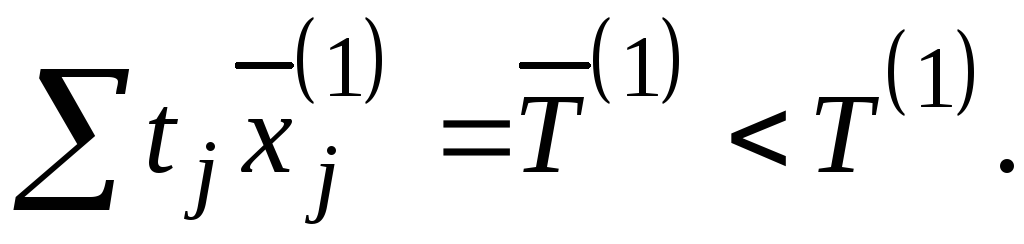
2. Если будет реализована чистая стратегия производства , то в зависимости от состояния «внешней среды» прибыль предприятия составит либо при уровне цен , либо при уровне цен .

Прибыль

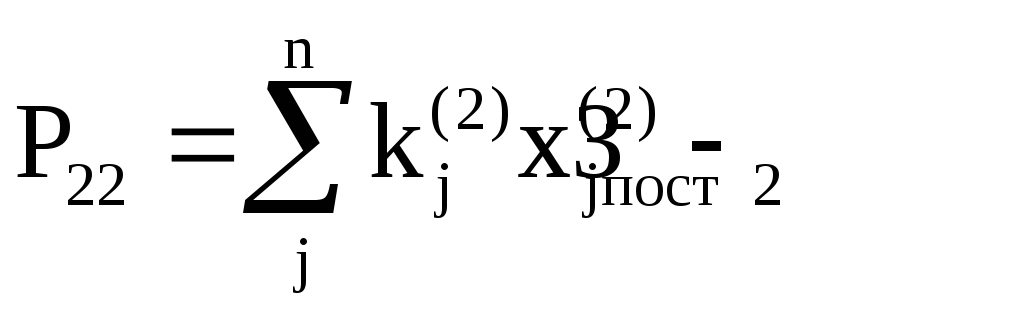
определяется решением задачи линейного программирования

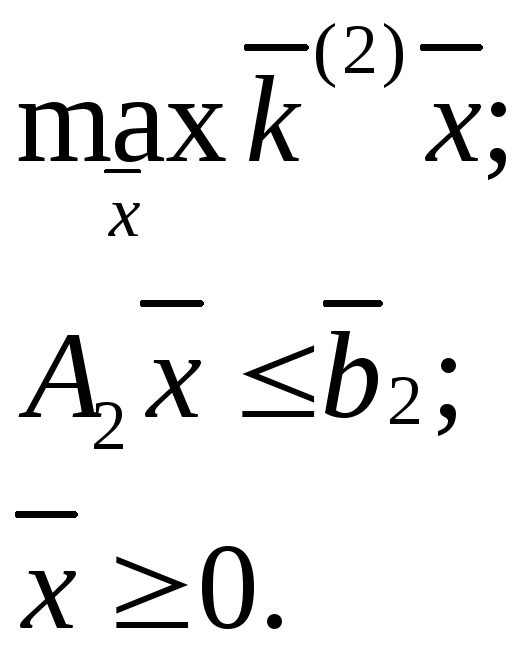
При этом трудоемкость годовой программы выпуска продукции равна

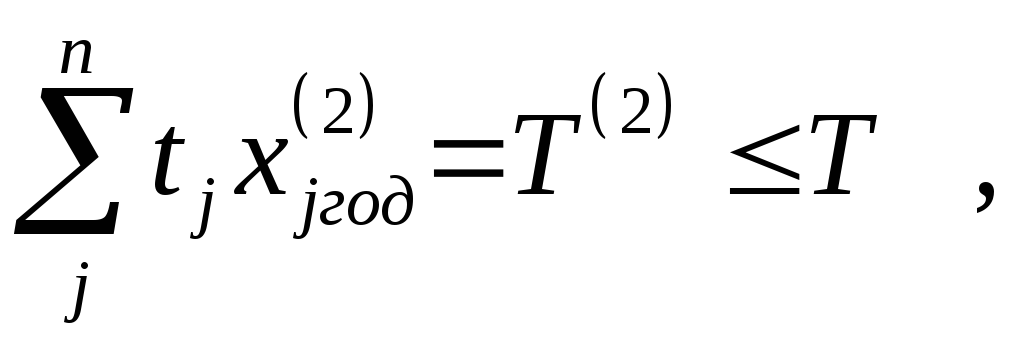
а производственные затраты составляют

Прибыль определяется как

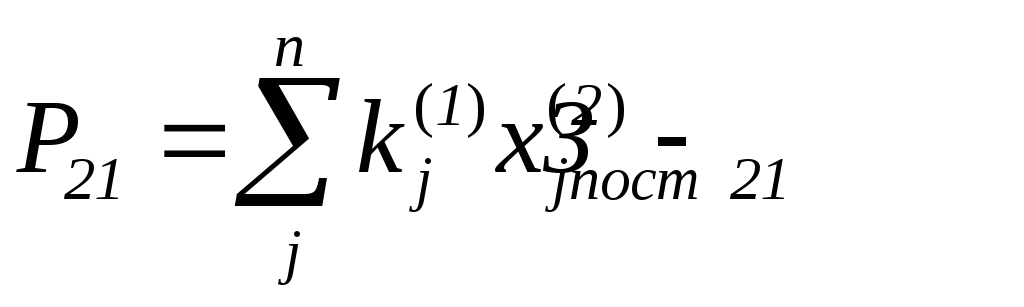
при условии, что производственные затраты не превышают расчетную величину :

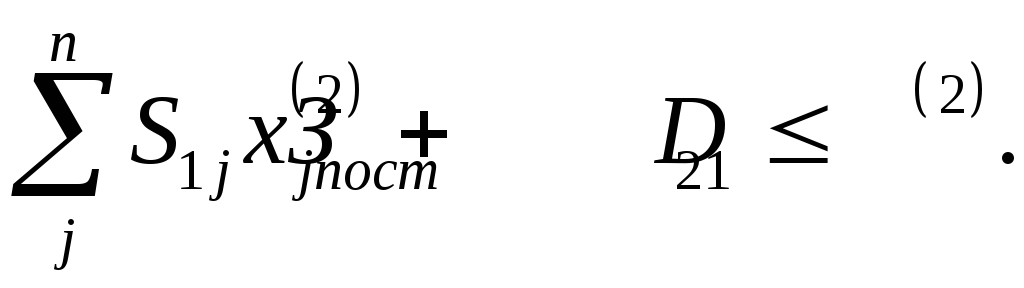
Если же ограничение по производственным затратам не выполняется, то прибыль рассчитывается как

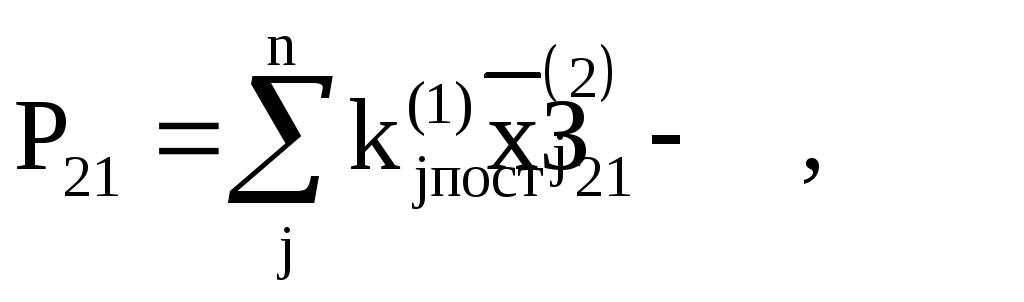
где

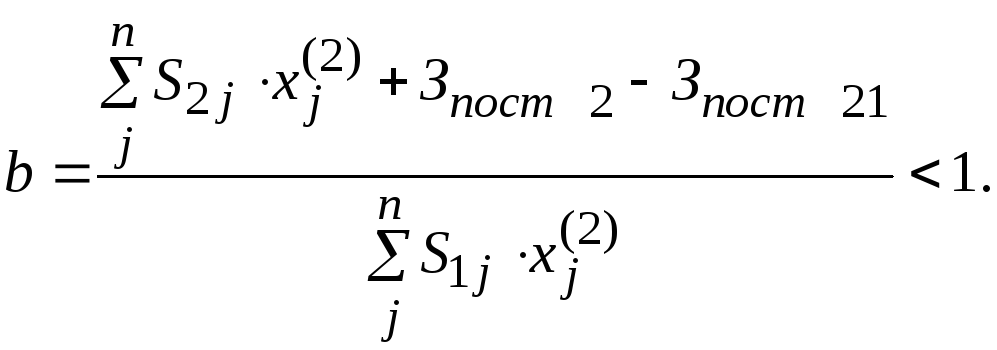
В этом случае трудоемкость годовой программы выпуска продукции будет составлять

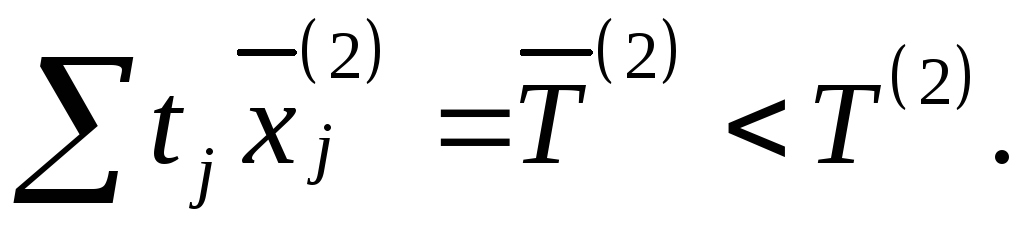
4.2. Расчет безрисковой стратегии производства на основе диверсификации ресурсов

Ставится задача: найти такое долевое распределение ресурсов между чистыми стратегиями производства при котором независимо от возможного уровня цен гарантированная прибыль была бы максимальной. Если принять допущение, что прибыли предприятия пропорциональны объемам производства, а те, в свою очередь, пропорциональны выделенным ресурсам, то для решения поставленной задачи необходимо решить сформулированную матричную игру, т.е. определить цену игры и обеспечивающую ее оптимальную стратегию

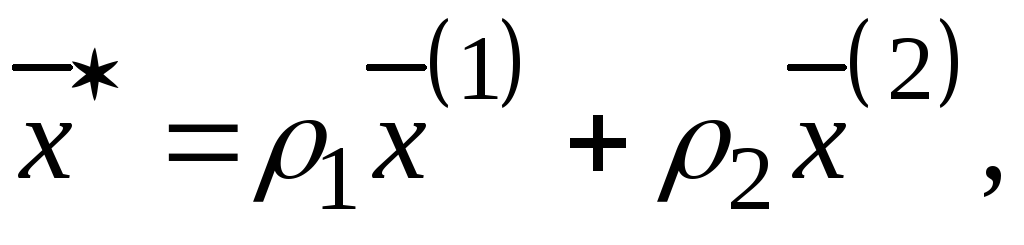
где .

Для решения этой задачи необходимо определить нижнюю и верхнюю цены игры:

В случае равенства нижней и верхней цен игры, что соответствует наличию седловой точки в рассматриваемой матричной игре, цена игры () - гарантированный максимальный результат - определяется одной из чистых стратегий , дающей максимальный результат из наихудших возможных исходов:

.

При этом

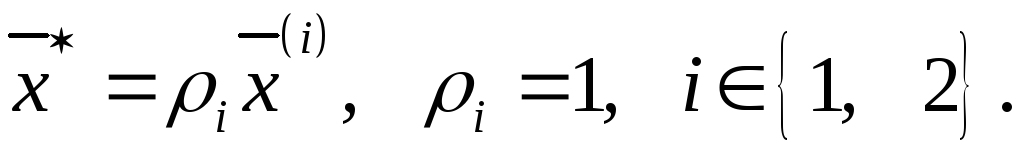
Итак, сформулируем заполненную матрицу возможных прибылей на основе проведенных расчетов и внесем данные в таблицу 5.

Таблица 5

Матрица возможных прибылей

Уровень цен Программа выпуска	Ц1	Ц2
	9021308	4087556
	3130752	4381347

α = max (4087556; 3130752) = 4087556

β = min (9021308; 4381347) = 4381347

Верхняя и нижняя цены игры равны, что свидетельствует о наличии седловой точки в данной матричной игре. Цена игра определяется одной из чистых стратегий, а именно:

Х₂ = 565,41