2. Разработать информационную технологию вычисления предела последовательности с точностью до . Начальное значение n принять равным 1. Вариант № 12

1. Разработать информационную технологию, позволяющую исследовать изменение значений поверхности и объема шарового сегмента при изменении высоты шарового сегмента от начального значения h₀ до конечного значения h_k с шагом h и радиуса шара от начального значения R₀ до конечного значения R_k с шагом R.

Внешний и внутренний циклы – с предусловием.

Для отладки принять: h₀ = 50, h_k = 100, h = 10; R₀ = 60, R_k = 70, R = 5.

2. Разработать информационную технологию вычисления приближенного значения корня уравнения с точностью до . Начальное приближение к корню принять равным 0,6.

.

Вариант № 13

1. Разработать информационную технологию, позволяющую исследовать изменение значений поверхности и объема шарового сегмента при изменении высоты шарового сегмента от начального значения h₀ до конечного значения h_k с шагом h и радиуса основания от начального значения r₀ до конечного значения r_k с шагом r.

Внешний и внутренний цикл – с постусловием.

Для отладки принять: h₀ = 10, h_k = 18, h = 4; r₀ = 12, r_k =16, r = 2.

2. Разработать информационную технологию вычисления предела последовательности 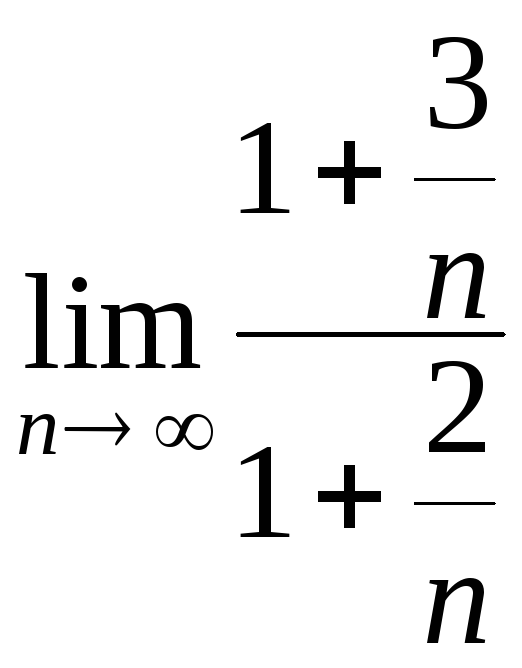точностью до . Начальное значение n принять равным 1.

Вариант № 14

1. Разработать информационную технологию, позволяющую исследовать изменение значений объема шарового пояса при изменении радиуса верхнего основания от начального значения r₁₀ до конечного значения r_1k с шагом r₁ и радиуса нижнего основания от начального значения r₂₀ до конечного значения r_2k с шагом r₂. Значение высоты шарового пояса не изменяется.

Внешний цикл – с предусловием, внутренний цикл – с постусловием.

Для отладки принять: r₁₀ = 5, r_1k = 10, r₁ = 2,5; r₂₀ = 20, r_2k = 32, r₂ = 4.

2. Разработать информационную технологию вычисления приближенного значения корня уравнения с точностью до . Начальное приближение к корню принять равным 1,2.

.

Вариант № 15

1. Разработать информационную технологию, позволяющую исследовать изменение значений поверхности и объема шарового сегмента при изменении высоты от начального значения h₀ до конечного значения h_k с шагом h и радиуса шара от начального значения R₀ до конечного значения R_k с шагом R. Значение радиуса основания шарового сегмента не изменяется.

Внешний цикл – с постусловием, внутренний цикл – с предусловием.

Для отладки принять: h₀ = 15, h_k =30, h = 5; R₀ = 15, R_k = 20, R = 1.

2. Разработать информационную технологию вычисления предела последовательности с точностью до . Начальное значение n принять равным 1. Вариант № 16

1. Разработать информационную технологию, позволяющую исследовать изменение расстояния между двумя точками на плоскости при изменении координаты x₁ от начального значения x₁₀ до конечного значения x_1k с шагом x₁ и координаты x₂ от начального значения x₂₀ до конечного значения x_2k с шагом x₂. Значение координат y₁ и y₂ не изменяется.

Внешний и внутренний циклы – с предусловием.

Для отладки принять: x₁₀ = 0,5, x_1k = 1,0, x₁ = 0,25; x₂₀ = 5,5, x_2k = 10,5, x₂ = 2,5.

2. Разработать информационную технологию вычисления приближенного значения корня уравнения с точностью до . Начальное приближение к корню принять равным 1.

Вариант № 17

1. Разработать информационную технологию, позволяющую исследовать изменение значений координат середины отрезка, который задан координатами начала и конца отрезка при изменении координаты y₁ от начального значения y₁₀ до конечного значения y_1k с шагом y₁ и координаты y₂ от начального значения y₂₀ до конечного значения y_2k с шагом y₂. Значение координат x₁ и x₂ не изменяется.

Внешний и внутренний цикл – с постусловием.

Для отладки принять: y₁₀ = 4,2, y_1k = 7,8, y₁ = 1,2; y₂₀ = 5, y_2k = 8, y₂ = 1.

2. Разработать информационную технологию вычисления предела последовательности функции с точностью до . Начальное значение n принять равным 1.

Вариант № 18

1. Разработать информационную технологию, позволяющую исследовать изменение значений координат точки, которая делит отрезок в отношении m:n, заданный координатами начала и конца отрезка при изменении координаты x₁ от начального значения x₁₀ до конечного значения x_1k с шагом x₁ и координаты y₂ от начального значения y₂₀ до конечного значения y_2k с шагом y₂. Значения координат y₁, x₂ и величин m, n не изменяются. Внешний цикл – с предусловием, внутренний цикл – с постусловием.

Для отладки принять: x₁₀ = 0,75, x_1k = 2,2, x₁ = 0,15; y₂₀ = 6, y_2k = 10, y₂ = 1.