4. Основные теоремы и формулы
Как правило, для определения вероятностей событий применяются не только непосредственные прямые методы, а и косвенные, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных. Вся теория вероятностей, в основном, и представляет собой систему таких косвенных методов, применение которых позволяет свести необходимый эксперимент к минимуму.
Суммой
двух событий
и
называют событие
,
состоящее в появлении хотя бы одного
из событий
и
(или
,
или
,
или
и
).
Теоремы сложения вероятностей
а) Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий
.
б) Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
.
Замечание. Следует иметь в виду, что когда события образуют сумму, то они объединяются союзом “или” и наоборот.
в)
Если события
образуют полную группу, то сумма их
вероятностей равна единице
.
г) Принцип целесообразности применения противоположных событий: если противоположное событие распадается на меньшее число вариантов, чем прямое событие, то имеет смысл при вычислении вероятности перейти к противоположному событию
.
Д) Исходя из того, что сумма событий состоит в появлении хотя бы одного из событий – слагаемых, в случае большого числа событий имеет смысл пользоваться другой формулой:
где
– вероятность непоявления
,
т.е.
,
– вероятность
непоявления
,
т.е.
,
– вероятность
непоявления
,
т.е.
,
– вероятность
непоявления
,
т.е.
.
Теоремы умножения вероятностей
Два события называют независимыми, если вероятность одного из них не зависит от того, произошло или нет другое событие.
В противоположном случае события называются зависимыми.
Вероятность события
,
найденная при условии, что событие
уже произошло, называется
условной
вероятностью
события
при условии выполнения
:
Условие независимости событий
и
:
.
Произведением
двух событий
и
называют событие
,
состоящее в одновременном появлении
событий
и
.
а) Вероятность произведения независимых событий равна произведению их вероятностей
б) Вероятность произведения зависимых событий равна произведению вероятности одного из них на условную вероятность другого
Замечание. Если события образуют произведение, то они объединяются союзом “и” и наоборот.
Формула полной вероятности
Следствием теоремы сложения и умножения вероятностей являются формула полной вероятности и формулы Бейеса.
Вероятность события
,
которое может наступить лишь при условии
появления одного из несовместных событий
,
образующих полную группу, равна сумме
произведений вероятностей каждого из
этих событий на соответствующую условную
вероятность события
.
Формула Бейеса
Если событие
уже произошло, то переоценить вероятность
каждой гипотезы при условии наступления
события
можно по формуле Бейеса.
Имеется полная группа
несовместных гипотез
.
Вероятности этих гипотез до опыта
известны и равны
.
Произведен опыт, в результате которого
появилось событие
.
Вероятность гипотезы
при условии наступления события
определяется формулой
,
,
где
– полная вероятность события
.
|
Пример 6. |
Вероятность попасть в мишень для первого стрелка равна 0,9, для второго – 0,8. Оба стрелка выполнили по одному выстрелу. Определить вероятность того, что мишень поражена. |
Решение.
Событие
– попадание первого стрелка, событие
– попадание второго стрелка.
,
.
Событие
– промах первого стрелка, событие
– промах второго стрелка.
,
.
Событие
– мишень поражена, хотя бы один стрелок
попал.
Событие
– оба стрелка промахнулись.
.
|
Пример 7. |
В одной урне 2 белых, 4 красных и 3 черных шара, в другой соответственно 3, 2 и 5 шаров. Вынимают по одному шару из каждой урны. Определить вероятность того, что они разные. |
Решение.
В урнах содержатся шары трех цветов. Варианты разных по цвету шаров могут быть такими:
-
1 урна
б
б
к
к
ч
ч
2 урна
к
ч
б
ч
б
к
Вероятность каждого из вариантов определяется по теореме умножения вероятностей независимых событий, а общая вероятность – их суммированием.
|
Пример 8. |
Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,44. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,6. |
Решение.
Обозначим вероятности
попадания 1-го и 2-го орудия через
и
,
тогда вероятности противоположных
событий будут
и
,
а вероятность только одного попадания
выразится соотношением:
;
,
,
,
|
Пример 9. |
На склад поступают утюги с двух заводов, первый из которых поставляет 70%, второй – 30% всего количества. Известно, что первый завод выпускает 90% продукции, способной прослужить гарантийный срок, а второй – 95%. Какова вероятность, что наугад взятый утюг прослужит гарантийный срок? |
Решение.
Событие
– утюг прослужит гарантийный срок.
-
Определение гипотез:
гипотеза
– утюг изготовлен первым заводом,
гипотеза
–
утюг изготовлен вторым заводом.
Гипотезы несовместны и образуют полную группу.
-
Определение доопытных вероятностей гипотез
;
.
.
-
Определение условных вероятностей
;
.
-
Определение полной вероятности
|
Пример 10. |
Есть 10 урн. В 3-х из них – по 4 белых, 6 черных шаров, в 5-ти – по 7 белых, 3 черных шаров, в 2-х – по 2 белых, 8 черных шаров. Наугад взятый шар оказался белым. Какова вероятность того, что он взят из 3-й группы урн? |
Решение.
Здесь, очевидно, нужно использовать формулу Бейеса, т.к. результат известен (шар оказался белым).
Событие
– шар оказался
белым.
-
Гипотеза
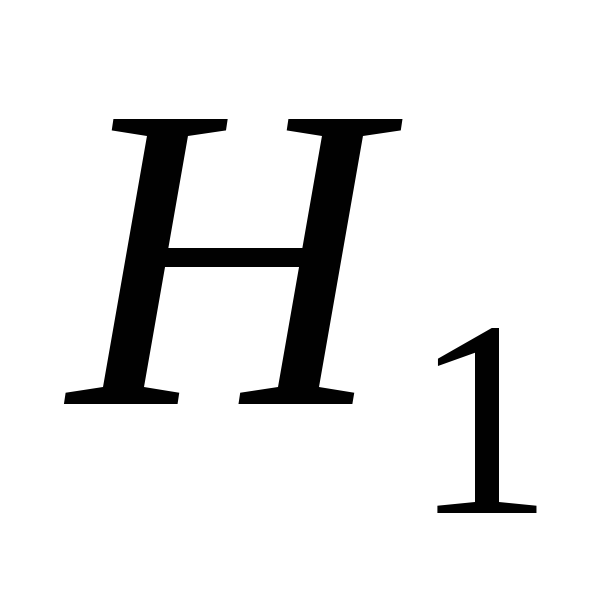– шар взят из первой группы урн.
Гипотеза
– шар взят из второй группы урн.
Гипотеза
– шар взят из третьей группы урн.
Гипотезы несовместны и образуют полную группу.
-
;
;
;
. -
;
;
. -
. -
.
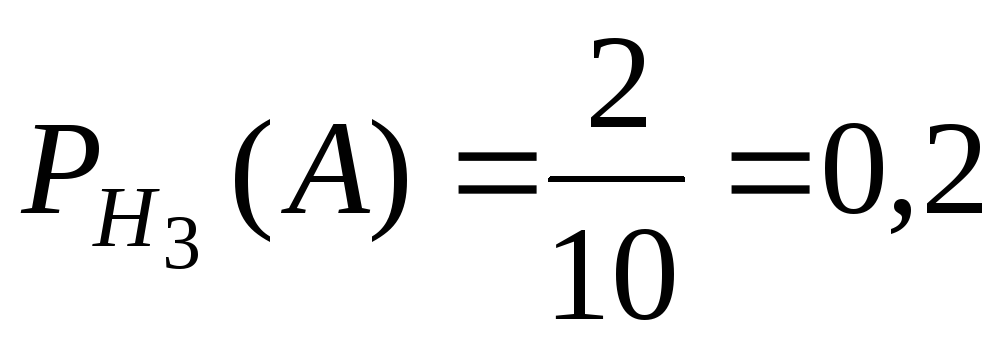