26. Композиция законов распределения

В приложениях часто рассматривается вопрос о распределении суммы нескольких случайных величин. Например, пусть Z=X+Y, тогда G(z) -интегральную функцию СВ Z можно определить по формуле

где: f(х,у)-дифференциальная функция системы слу­чайных величин (X,Y);

область D - полуплоскость, ограниченная сверху прямой y= z-x.

Отсюда g(z) = G'(z) = ∫f(x, z - x)dx.

Если Х и Y независимы, то говорят о композиции законов распределения случайных величин и дифференциальная фун­кция СВ Z определяется как g(z)=f₁ (x) f₂(z-x)dx, где f ,(х) и f₂(y) дифференциальные функции СВ X и Y соответственно.

Если возможные значения аргументов неотрицатель­ны, то дифференциальную функцию СВ Z определяют по формуле

или

19. Равномерный закон распределения.

СВ X распределена по равномерному (прямоугольному) закону, если все значения СВ лежат внутри некоторого интервала и все они равновероятны (точнее обладают одной плотностью вероятности).Например, если весы имеют точность 1г и полученное значение округляется до ближайшего целого числа k, то точный вес можно считать равномерно распределенной СВ на интервале (k-0,5; k+0,5).

Дифференциальная функция равномерного закона на интервале (α,β) (рис. 11):

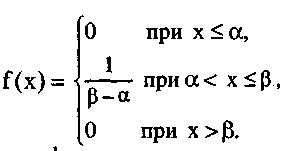
Интегральная функция равномерного закона на интервале (α,β) (рис. 11):

Рис. 11. 1). Дифференциальная функция. 2). Интегральная функция.

Основные числовые характеристики равномерного закона:

1. Математическое ожидание

М(Х) совпадает, в силу симметрии распределения, с медианой.

2. Моды равномерное распределение не имеет.

3.Дисперсия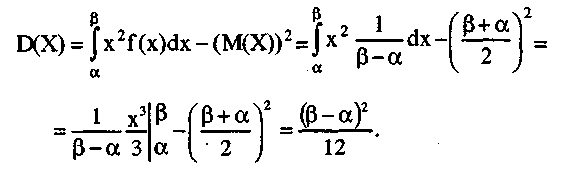

Отсюда, среднее квадратическое отклонение

4. Третий центральный момент

поэтому распределение симметрично относительно М(Х).

5.

Четвёртый центральный момент

6. Вероятность попадания СВ в заданный интервал (а;b). Пусть СВ X распределена по равномерному закону,

тогда (рис.12)

Рис.12. Вероятность попадания равномерно распределенной СВХ в (а;b).

21. Нормальный закон распределения

Нормальный закон распределения (рис. 14) играет исклю­чительную роль в теории вероятностей. Это наиболее часто встречающийся закон распределения, главной особенностью которого является то, что он является предельным законом, к которому, при определённых условиях, приближаются другие законы распределения.

Дифференциальная функция нормального закона имеет вид (рис. 14)

Числовые характеристики нормального закона:

1. Математическое ожидание характеризует центр распределения

, где e^x=exp(x);

2. Дисперсия характеризует форму распределения

Свойства дифференциальной функции нормального закона:

1. Область определения: D_f = R;

2. Ось ОХ - горизонтальная асимптота;

3. х = а±σ - две точки перегиба;

4. Максимум в точке с координатами (а; 1/(σ√2π);

5. График симметричен относительно прямой х=а;

6. Моменты:

μ₁=μ₃=…=μ_2k+1=…=0,

μ₂=σ², μ₄=3σ⁴,

Sk=μ³/σ³=0, Ex=μ⁴/σ⁴-3=0

7. Вероятность попадания нормально распределенной случайной величины в заданный интервал определяется, по свойству интегральной функции

где

интегральная функция нормального закона (рис.14); Ф(х)- функция Лапласа.

Свойства интегральной функции нормального закона:

1. Ф* (-∞)=0;

2. Ф*(+)=1;

3. Ф*(x)=1/2+Ф(x);

4. Ф*(-x)=1-Ф*(x).