лабораторная работа / Л1

Министерство Образования Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Кафедра ТК

Отчет по лабораторной работе №1

по предмету «Основы теории управления»

на тему: Динамические звенья и их характеристики во временной области

Вариант №2

Выполнили:

.

Уфа 2008

1. Цель работы

Целью работы является изучение временных характеристик типовых динамических звеньев с использованием автоматизированных средств моделирования на ПК – MATLAB, SIMULINK.

Задание на выполнение работы:

№	Апериод звено		Апериодич. звено 2 пор. (колеб. звено)			Интегр звено	Изодр. звено		Реальное диф. звено		Инерц.-форс Звено
	K	T [с]	K	T [с]	ξ	K	K1	K2	K	τ [с]	K	T0 [с]	T [с]
2	3	0,3	2	0,3	1,5 (0,15)	3	3	1	3	0,3	3	3	1,2

2. Теоретическая часть

Рассматривается система автоматического управления (САУ), описываемая линейным дифференциальным уравнением вида:

(1)

где u(t) – входной процесс; y(t) – выходной процесс a_i , b_i , – постоянные коэффициенты; п, т (п >= т) – постоянные числа.

Если ввести обозначение р для оператора дифференцирования , то можно записать (1) в операторной форме:

(2)

откуда получается:

где А(р) и В(р) – полиномы из формулы (2).

Выражение (2) по виду совпадает с определением передаточной функции (ПФ) как отношения преобразования по Лапласу выходной переменной к преобразованию по Лапласу входной переменной при нулевых начальных условиях:

(3)

где s – комплексная переменная.

Комплексные числа, являющиеся корнями многочлена B(s), называются нулями передаточной функции, а корни многочлена А(s) –полюсами.

Временные характеристики динамического звена представляют собой зависимость выходного сигнала системы от времени при подаче на ее вход некоторого типового воздействия. Обычно выполняется анализ выхода системы на единичный скачок (функция Хевисайда) и импульсную функцию (функция Дирака или δ-функция).

Единичный скачок 1(t) определяется условиями:

Реакция САУ на единичный скачок называется переходной функцией системы и обозначается h(t). При неединичном ступенчатом воздействии g(t)=N·1(t), где N = const, в соответствии с принципом суперпозиции выходная реакция системы будет

Импульсная функция δ(t) определяется условиями:

Очевидно:

Реакция САУ на импульсную функцию называется импульсной переходной функцией системы (функцией веса) и обозначается w(t).

Импульсная и переходная функции системы связаны соотношением

2.1. Позиционные звенья

2.1.1. Апериодическое (инерционное) звено первого порядка

Передаточная функция данного звена имеет вид .

Временные характеристики:

1) Переходная.

Переходная – получаемая с помощью функции step в MATLAB:

Переходная функция имеет вид .

Постоянная времени T переходной функции h(t) определяет наклон касательной в начале кривой, т.е. величина T характеризует степень инерционности динамического звена.

2) Весовая.

Весовая (импульсная переходная) - получаемая с помощью функции impulse в MATLAB:

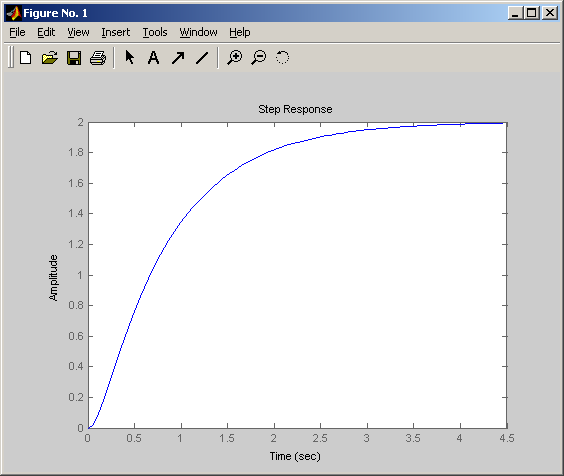
2.1.2. Апериодическое звено второго порядка

Передаточная функция звена имеет вид

где - коэффициент затухания.

Эта передаточная функция может быть записана также в виде

где T₁ и T₂ соответствующие постоянные времени, определяемые корнями характеристического уравнения

Определение корней характеристического уравнения

Временные характеристики:

1) Переходная.

2) Весовая (импульсная переходная)

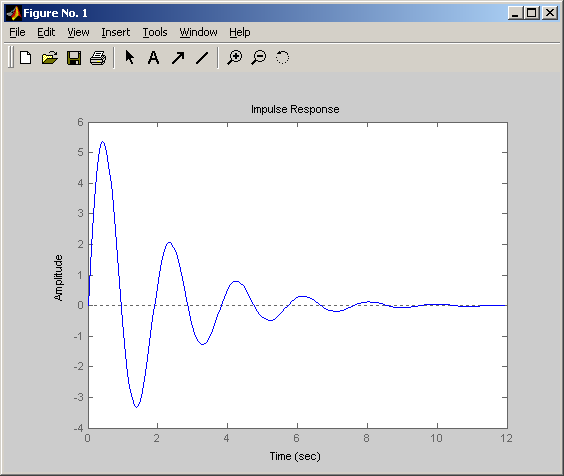
2.1.3. Колебательное звено второго порядка

Передаточная функция имеет вид

(1)

Величина в (1) представляет частоту собственных колебаний.

Временные характеристики:

1) Переходная.

Снижение параметра затухания ξ

приводит к повышению колебательности

переходного процесса.

2) Весовая (импульсная переходная).

2.2. Интегрирующие звенья

2.2.1. Идеальное интегрирующее звено

Данное звено имеет передаточную функцию

Временные характеристики:

1) Переходная.

Переходная функция идеального интегрирующего звена

2) Весовая (импульсная переходная)

2.2.2. Изодромное звено (пропорционально-интегрирующее звено)

Это звено имеет передаточную функцию

т.е. его можно представить как параллельное соединение интегрирующего и пропорционального (безынерционного) звеньев. После простых преобразований это звено можно также записать в виде:

(2)

где (1+τs) - форсирующее звено, τ =K₂/K_1.

Таким образом, в соответствии с (2) изодромное звено может быть также представлено как последовательное соединение интегрирующего и форсиру-ющего звеньев.

Временные характеристики:

1) Переходная.

Переходная функция пропорционально-интегрирующего звена

2) Весовая (импульсная переходная).

2.3. Дифференцирующие звенья

2.3.1. Реальное дифференцирующее звено

Передаточная функция звена

,

Временные характеристики:

1) Переходная.

Переходная функция звена имеет вид

2) Весовая (импульсная переходная).

2.3.2. Инерционно-форсирующее (реальное форсирующее) звено

Передаточная функция звена

(3)

В установившемся режиме выходная величина данного звена пропорциональна входной, т.е. оно может быть отнесено к звеньям позиционного типа.

При η >> 1 оно по своим свойствам приближается к форсирующему звену.

Таким образом, в соответствии с (3) инерционно-форсирующее звено может быть также представлено как последовательное соединение инерционного и форсиру-ющего звеньев.

Временные характеристики:

1) Переходная. 2) Весовая (импульсная переходная).

3. Выводы

В проделанной лабораторной работе были изучены временные характеристики 3-х типов динамических звеньев: позиционных, интегрирующих и дифференцирую-щих (с использованием автоматизированных средств моделирования на ПК – MATLAB).

12