
- •Введение
- •Требования к выполнению и оформлению контрольной работы по информатике для студентов заочной формы обучения
- •Требования к содержанию работы
- •Требования к оформлению работы
- •Оценивание контрольной работы
- •Варианты контрольных работ
- •Вопросы к контрольной работе по информатике
- •Тема 1. Основы информационной культуры
- •Тема 2. Техническая база информационных технологий
- •Тема 3. Алгоритмизация и программирование
- •Тема 4. Технология программирования в среде turbobasic (qbasic или turbopascal)
- •Тема 5. Системное программное обеспечение компьютера
- •Тема 6. Текстовый процессор ms word
- •Тема 7. Табличный процессор ms еxcel
- •Тема 8. Система управления базами данных
- •Тема 9. Графические редакторы
- •Тема 10. Компьютерные сети
- •Тема 11. Защита информации
- •Варианты задач
- •1. Даны два числа X и y. Вычислить
- •Термины
- •Примеры по алгоритмизации и программированию Алгоритмы линейной структуры
- •Алгоритмы разветвляющейся структуры
- •Алгоритмы циклической структуры
- •Пример оформления контрольной работы
- •Инструкция по безопасной эксплуатации персональных компьютеров (пк)
- •Общие требования безопасности
- •Требования безопасности перед началом работы
- •Требования безопасности во время работы
- •Используемая литература и источники:
- •Список литературы а) основная литература:
- •Б) дополнительная литература:
- •В) справочная литература:
- •Г) учебно-методическая литература:
- •Д) основные периодические издания:
- •Алгоритмы линейной структуры……………………………..24 Алгоритмы разветвляющейся структуры…………………...25 Алгоритмы циклической структуры…………………………30
Примеры по алгоритмизации и программированию Алгоритмы линейной структуры
Вычислительный процесс, в котором все действия выполняются последовательно в порядке их записи строго по одному разу, называется линейным. К такому процессу сводится вычисление значения величин, задаваемых формулами. Рассмотрим алгоритм линейной структуры.
З адача
1. Определить площадь треугольника
по формуле Герона S=р(р-а)(р-в)(р-с),
где a,b,c
– длины сторон, р – полупериметр
треугольника.
адача
1. Определить площадь треугольника
по формуле Герона S=р(р-а)(р-в)(р-с),
где a,b,c
– длины сторон, р – полупериметр
треугольника.
Схема алгоритма представлена ниже.
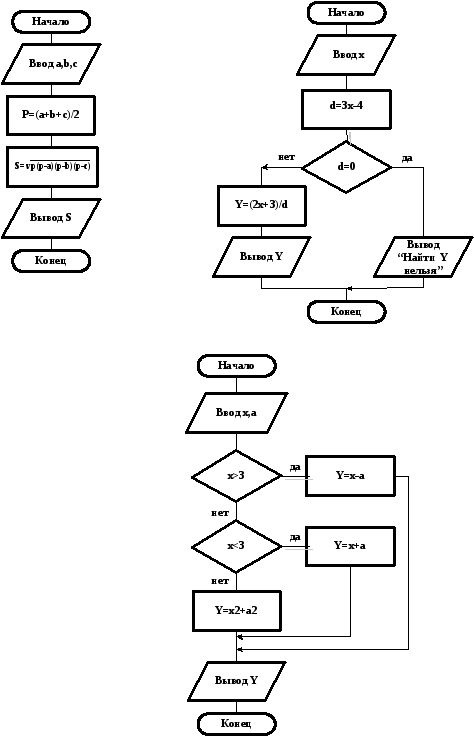
Рис.1. Схема алгоритма решения задачи 1.
Программа на Паскале решения этой задачи выглядит так:
Program Prim_1; {заголовок программы}
Var A, B, C, S, P: Real; {блок описания данных}
Begin {начало операторов программы}
Read(A,B,C); {ввод трех чисел с клавиатуры }
WriteLn(A,B,C); {вывод этих чисел на экран для контроля}
P:=(A+B+C)/2; {нахождение полупериметра}
S:=Sqrt(P*(P-A)*(P-B)*(P-C)); {нахождение площади }
WriteLn('S=',S:8:3) {вывод результата}
End. {конец программы}
Все операторы заканчиваются знаком “;”. Перед оператором END точку с запятой не ставят.
В этой программе, конечно же, для полной строгости нужно сделать проверку на корректность исходных данных (нет ли среди чисел отрицательных, могут ли три заданных положительных числа быть сторонами треугольника). Для того чтобы продемонстрировать линейный алгоритм, сделаем в этот раз исключение и не станем проверять исходные данные.
Этот же алгоритм решения задачи записывается на Бейсике следующим образом:
10 Input A,B,C
20 Print A,B,C
20 P=(A+B+C)/2
30 S=Sqr(P*(P-A)*(P-B)*(P-C))
40 Print “S=”;S
50 End
Алгоритмы разветвляющейся структуры
Разветвляющимся называется вычислительный процесс, реализация которого происходит по одной из нескольких заранее предусмотренных последовательностей действий (ветвей). Выбор ветви зависит от выполнения или невыполнения заданного условия. По одной из ветвей может не быть никаких действий. Это называется обходом.
Задача 2. Составить схему алгоритма вычисления значения y=(2x+3)/(3x-4).
На первый взгляд, алгоритм нахождения значения y кажется линейным, но это не так. В алгоритме необходимо проверить условие: равен ли нулю знаменатель при данном значении x. Если это условие выполняется, то идем по стрелке "да" и выводим сообщение о невозможности вычисления y. Если условие не выполняется, то переходим по стрелке "нет" к блоку, в котором вычисляется значение y.
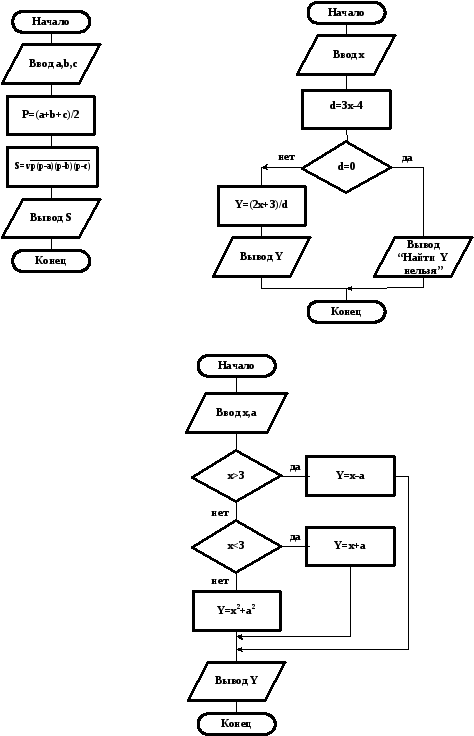
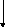

Рис.2. Схема алгоритма решения задачи 2.
Приведем программы на Паскале и Бейсике для задачи 2.
Program Prim_2; {заголовок программы}
Var X, D: Integer; {блок описания данных}
Y : Real;
Begin {начало операторов программы}
Read(X); {ввод значения Х с клавиатуры }
WriteLn('X=',Х); {вывод Х на экран для контроля}
D:=(3*X-4); {нахождение знаменателя}
WriteLn('D=',D); {вывод D на экран для контроля}
If D=0 Then {если знаменатель=0, то делать}
Writeln('Найти Y нельзя') {вывод сообщения}
Else {иначе выполнить}
Begin {открытие блока}
Y:=(2*X+3)/D; {нахождение Y }
Writeln('Y=',Y:8:2) {вывод результата}
End {закрытие блока}
End. {конец программы}
Эта же задача может быть записана на Бейсике следующим образом:
10 Input X%
20 Print "X=";X%
30 D%=(3*X%-4)
40 If D%=0 Then Print "Нельзя найти Y" Else Y=(2*X%+3)/D% : Print Y
50 End
Целый тип в Бейсике может задаваться через имена переменных. Для этого используется знак %, который ставится в конце имени. Например, переменная X имеет вещественный тип, а переменная X% - целый тип.
Задача 3. Вычислить
 x
+ a
, если x
< 3
x
+ a
, если x
< 3
y = x - a , если x > 3
x2 + a2 , если x = 3
Имеются три формулы для вычисления y. Исходными данными в задаче являются переменные x и a. Выбор той или иной формулы зависит от заданных условий. Можно начать алгоритм с проверки любого условия из заданных. В разветвляющемся алгоритме должны получиться три ветви (каждая ветвь для соответствующей формулы). Это обеспечивается проверкой двух условий. Выполнение третьего условия следует автоматически из невыполнения двух других.
Предлагается следующая блок-схема решения этой задачи.
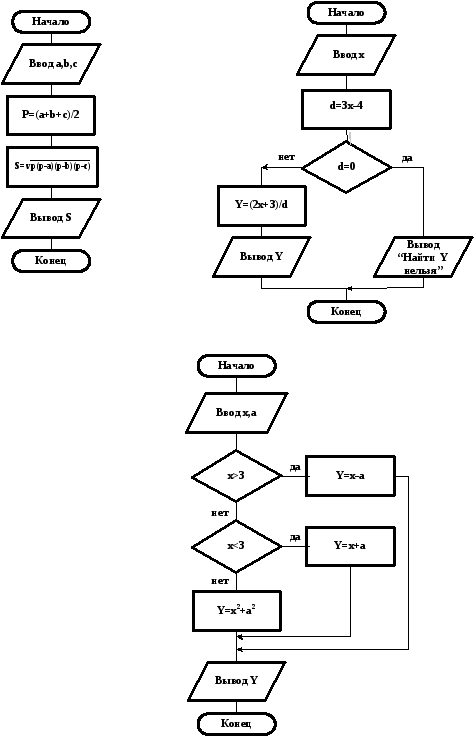
Рис.3. Схема алгоритма решения задачи 3.
Программа на Паскале представлена ниже.
Program Prim_3; {заголовок программы}
Var X : Integer; {блок описания данных}
Y, A: Real;
Begin {начало операторов программы}
Read(X); {ввод целого числа Х с клавиатуры}
WriteLn('X=',Х); {вывод Х на экран для контроля}
Read(A); {ввод вещественного числа A с клавиатуры}
WriteLn('A=',A:6:2); {вывод A на экран для контроля}
If X>3 Then {если X>3, то делать}
Y:=X-A
Else {иначе выполнить}
If X<3 Then Y:=X+A
Else Y:=X*X+Y*Y; {иначе выполнить}
Writeln('Y=',Y:8:2) {вывод результата}
End. {конец программы}
Решение этой задачи может быть записано на Бейсике следующим образом:
10 Input X%,A
20 Print ("X=";X%)
30 Print ("A=";A)
40 If X%>3 Then Y=X%-A : GOTO 60
50 If X%<3 Then Y=X%+A Else Y=X%*X%+A*A
60 Print ("Y=";Y)
70 End
Задача 4. Даны целые числа x, y, z. Вычислить u=min(x, max( y, z)).
В этой задаче сначала нужно найти наибольшее число из y и z. Найденное наибольшее число запоминается в переменной r. Затем находится наименьшее число из x и r.
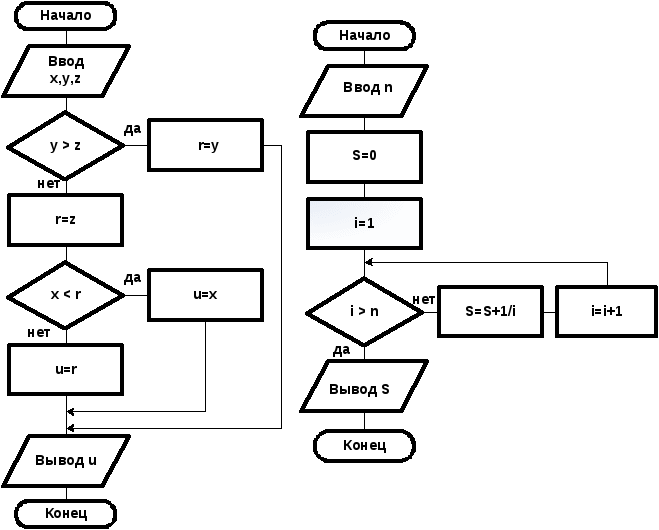
Рис.4. Схема алгоритма решения задачи 4.
Приведем соответствующие программы.
Program Prim_4; {заголовок программы}
Var X, Y, Z,R,U: Integer; {блок описания данных}
{Все переменные в программе целого типа}
Begin {начало операторов программы}
WriteLn('Введите три целых числа X, Y, Z ’ );
Read(X,Y,Z); {ввод значения Х с клавиатуры}
WriteLn('X=',Х,’Y=’,Y,’Z=’,Z); {вывод Х на экран для контроля}
If Y>Z Then {если Y>Z, то делать}
R:=Y
Else {иначе выполнить}
R:=Z;
If X<R Then
U:=X
Else
U:=R;
Writeln('U=',U:6) {вывод результата}
End. {конец программы}
Алгоритм на Бейсике выглядит так:
10 Input X%,Y%,Z%
20 Print ("X=";X%)
30 Print ("Y=";Y%)
40 Print ("Y=";Y%)
50 If Y%>Z% Then R%=Y% Else R%=Z%
60 If X%<R% Then U%=X% Else U%=R%
60 Print ("U=";U%)
70 End
