лабораторная работа / Методичка 5 (1)

Министерство образования и науки Российской Федерации

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Метод гармонической линеаризации

Методические указания к лабораторной работе по курсу «Теория автоматического управления» для студентов специальности 210100

Одобрено

редакционно –издательским советом

Балаковского интститута техники,

технологии и управления

Балаково 2004

Цель работы: изучение нелинейных систем с помощью метода гармонической линеаризации (гармонического баланса), определение коэффициентов гармонической линеаризации для различных нелинейных характеристик. Получение навыков по нахождению параметров симметричных колебаний постоянной амплитуды и частоты (автоколебаний), используя алгебраический, частотный способы, а также с помощью критерия Михайлова.

ОСНОВНЫЕ СВЕДЕНИЯ

Метод гармонической линеаризации относится к приближенным методам исследования нелинейных систем. Он позволяет достаточно просто и с приемлемой точностью оценивать устойчивость нелинейных систем, определять частоту и амплитуду установившихся в системе колебаний.

Предполагается, что исследуемая нелинейная САУ может быть представлена в следующем виде

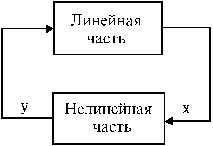
Рис.1.

причем нелинейная часть должна иметь одну нелинейность

(1)

Эта нелинейность может быть как непрерывной, так и релейной, однозначной или гистерезисной.

Любую функцию или сигнал можно разложить в ряд по системе линейно-независимых, в частном случае ортонормированных функций. В качестве такого ортогонального ряда может быть использован ряд Фурье.

Разложим в ряд Фурье выходной сигнал нелинейной части системы

, (2)

здесь - коэффициенты Фурье,

,

,

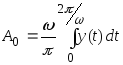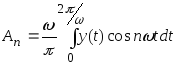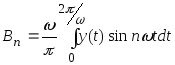(3)

Таким образом, сигнал согласно (2) может быть представлен в виде бесконечной суммы гармоник с возрастающими частотами и т. д. Этот сигнал поступает на вход линейной части нелинейной системы.

Обозначим передаточную функцию линейной части

, (4)

причем степень полинома числителя должна быть меньше степени полинома знаменателя. В этом случае АЧХ линейной части имеет вид

Рис.2.

где 1 - не имеет полюсов, 2 - имеет полюс или полюса.

Для АЧХ справедливо записать

(5)

Таким образом, линейная часть нелинейной системы является фильтром высоких частот. В этом случае линейная часть будет пропускать без ослабления только низкие частоты, высокие же по мере роста частоты будут существенно ослабляться.

В методе гармонической линеаризации делается предположение о том, что линейная часть системы будет пропускать только постоянную составляющую сигнала и первую гармонику. Тогда сигнал на выходе линейной части будет иметь вид

(6)

Этот сигнал проходит по всему замкнутому контуру системы рисунку 1 и на выходе нелинейного элемента без учета более высоких гармоник, согласно (2) имеем

(7)

При исследовании нелинейных систем с помощью метода гармонической линеаризации возможны случаи симметричных и несимметричных колебаний. Рассмотрим случай симметричных колебаний. Здесь и.

Введем следующие обозначения

,

.

Подставив их в (7), получим . (8)

С учетом того, что

,

, где ,

получим

. (9)

Согласно (3) и (8) при

,

. (10)

Выражение (9) является гармонической линеаризацией нелинейности устанавливает линейную связь входной переменной и выходной при . Величины и называются коэффициентами гармонической линеаризации.

Необходимо отметить, что уравнение (9) является линейным для конкретных величин и (амплитуды и частоты гармонических колебаний в системе). Но в целом оно сохраняет нелинейные свойства, так как коэффициенты различны для различных и . Эта особенность и позволяет исследовать с помощью метода гармонической линеаризации свойства нелинейных систем [ Попов Е.П.].

В случае несимметричных колебаний гармоническая линеаризация нелинейности приводит к линейному уравнению

, (11)

где

,

,

. (12)

Так же как и уравнение (9), линеаризованное уравнение (11) сохраняет свойства нелинейного элемента, так как коэффициенты гармонической линеаризации , , а так же постоянная составляющая зависят и от смещения и от амплитуды гармонических колебаний .

Уравнения (9) и (11) позволяют получить передаточные функции гармонически линеаризованных нелинейных элементов. Так для симметричных колебаний

, (13)

при этом частотная передаточная функция

(14)

зависит только от амплитуды и не зависит от частоты колебаний в системе.

Необходимо отметить, что если нечетно-симметричная нелинейность однозначна, то в случае симметричных колебаний в соответствии с (9) и (10) получим, что , (15)

так как

(16)

и линеаризованная нелинейность имеет вид

. (17)

Для неоднозначных нелинейностей (с гистерезисом) интеграл в выражении (16) не равен нулю, вследствие различия в поведении кривой при возрастании и убывании , поэтому справедливо полное выражение (9).

Найдем коэффициенты гармонической линеаризации для некоторых нелинейных характеристик. Пусть нелинейная характеристика имеет вид релейной характеристики с гистерезисом и зоной нечувствительности. Рассмотрим, как гармонические колебания проходят через нелинейный элемент с такой характеристикой.

При выполнении условия , то есть если амплитуда входного сигнала меньше зоны нечувствительности , то сигнал на выходе нелинейного элемента отсутствует. Если же амплитуда , то реле переключается в точках A, B, C и D. Обозначим и .

Тогда

,

. (18)

При вычислении коэффициентов гармонической линеаризации следует иметь ввиду, что при симметричных нелинейных характеристиках интегралы в выражениях (10) находятся на полупериоде (0, ) с последующим увеличением результата в два раза. Таким образом

,



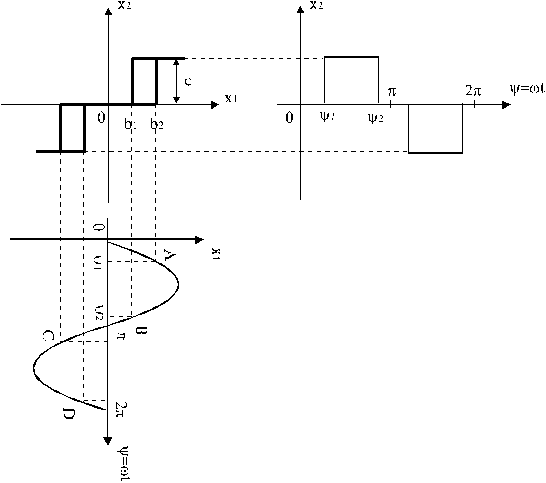
Рис.3.

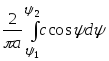. (19)

Тогда

,

. (20)

Для нелинейного элемента с релейной характеристикой и зоной нечувствительности

,

. (21)

Для нелинейного элемента, имеющего релейную характеристику с гистерезисом

,

. (21)

Аналогично могут быть получены коэффициенты гармонической линеаризации для других нелинейных характеристик.

Рассмотрим два способа определения симметричных колебаний постоянной амплитуды и частоты (автоколебаний) и устойчивости линеаризованных систем: алгебраический и частотный. Сначала рассмотрим алгебраический способ. Для замкнутой системы Рис.1 передаточная функция линейной части равна

.

Запишем гармонически линеаризованную передаточную функцию нелинейной части

.

Характеристической уравнение замкнутой системы имеет вид

. (22)

Если в исследуемой системе возникают автоколебания, то это говорит о наличии двух чисто мнимых корней в ее характеристическом уравнении. Поэтому подставим в характеристическое уравнение (22) значение корня .

. (23)

Представим

.

Получим два уравнения, определяющих искомую амплитуду и частоту

,

. (24)

Если в решении возможны вещественные положительные значения амплитуды и частоты , то в системе могут возникнуть автоколебания. Если же амплитуда и частота не имеет положительных значений, то автоколебания в системе невозможны.

Рассмотрим пример 1. Пусть исследуемая нелинейная система имеет вид

Рис.4.

В этом примере нелинейный элемент представляет собой чувствительный элемент с релейной характеристикой, для которого коэффициенты гармонической линеаризации

,

. (25)

Исполнительное устройство имеет передаточную функцию вида

. (26)

Передаточная функция объекта регулирования равна

. (27)

Передаточная функция линейной части системы

, (28)

где .

На основании (22), (25) и (28) запишем характеристическое уравнение замкнутой системы

, (29)

откуда

,

. (30)

Пусть 1/сек, сек, сек, в.

В этом случае параметры периодического движения равны

7,071 ,

в.

Рассмотрим способ определения параметров автоколебаний в линеаризованной САУ с помощью критерия Михайлова. Способ основан на том, что при возникновении автоколебаний система будет находиться на границе устойчивости и годограф Михайлова в этом случае будет проходить через начало координат.

В примере 2 найдем параметры автоколебаний при том условии, что нелинейный элемент в системе Рис.4 представляет собой чувствительный элемент, имеющий релейную характеристику с гистерезисом, для которого коэффициенты гармонической линеаризации

,

.

Линейная часть осталась неизменной.

Запишем характеристическое уравнение замкнутой системы

.

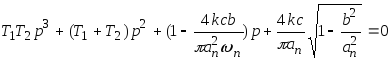Годограф Михайлова получается заменой .

.

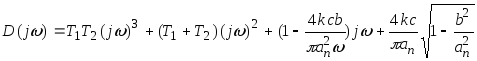Задача заключается в том, чтобы подобрать такую амплитуду колебаний , при которой годограф пройдет через начало координат. Необходимо отметить, что при этом текущая частота , так как именно в этом случае кривая пройдет через начало координат.

Расчеты, проведенные в MATHCAD 7 при 1/сек, сек, сек, в и в, дали следующие результаты. На Рис.5 годограф Михайлова проходит через начало координат. Для повышения точности расчетов увеличим нужный фрагмент графика. На Рис.6 приведен фрагмент годографа, увеличенный в окрестности начала координат. Кривая проходит через начало координат при в.

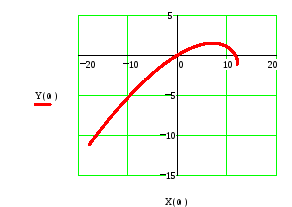
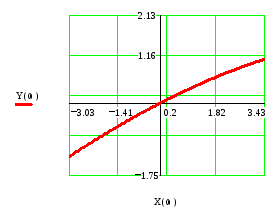
_{Рис.5. Рис.6.}

_{Частоту колебаний при этом можно найти из условия равенства нулю модуля . Для частот}

_{значения модуля сведены в таблицу}

Таким образом, частота колебаний 6,38 . Необходимо отметить, что точность расчетов легко может быть увеличена.

Полученное периодическое решение, определяемое значением амплитуды и частоты , необходимо исследовать на устойчивость. Если решение устойчиво, то в системе имеет место автоколебательный процесс (устойчивый предельный цикл). В противном случае предельный цикл будет неустойчивым.

Проще всего для исследования устойчивости периодического решения использовать критерий устойчивости Михайлова в графическом виде. Было установлено, что при кривая Михайлова проходит через начало координат. Если дать малое приращение , то кривая займет положение либо выше нуля, либо ниже. Так в последнем примере дадим приращение в, то есть и . Положение кривых Михайлова показано на Рис.7.

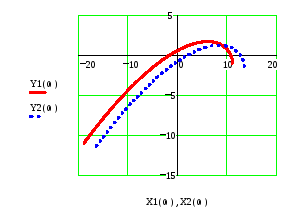
Рис.7.

При кривая проходит выше нуля, что говорит об устойчивости системы и затухающем переходном процессе. При кривая Михайлова проходит ниже нуля, система является неустойчивой и переходный процесс является расходящимся. Таким образом, периодическое решение с амплитудой в и частотой колебаний 6,38 устойчиво.

Для исследования устойчивости периодического решения может быть использован и аналитический критерий, получаемый из графического критерия Михайлова. Действительно, чтобы узнать пойдет ли кривая Михайлова при выше нуля достаточно посмотреть, куда будет перемещаться точка кривой Михайлова, которая при находится в начале координат.

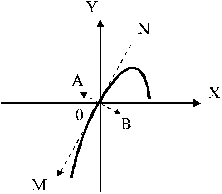
Рис.8.

Если разложить перемещение этой точки по координатным осям X и Y, то для устойчивости периодического решения вектор, определяемый проекциями на координатные оси

и ,

должен быть расположен справа от касательной MN к кривой Михайлова, если смотреть вдоль кривой в сторону возрастания , направление которой определяется проекциями

и .

Аналитическое условие устойчивости запишем в следующем виде

. (31)

В этом выражении частные производные берутся по текущему параметру кривой Михайлова

,

в точке .

Необходимо отметить, что аналитическое выражение критерия устойчивости (31) справедливо только для систем не выше четвертого порядка, так как например для системы пятого порядка в начале координат условие (31) может выполняться, а система будет неустойчивой

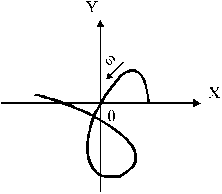
Рис.9.

Применим критерий (31) для исследования устойчивости периодического решения, полученного в примере 1.

Так как

,

,

то

, ,