лабораторная работа / Методичка 5 (1)

, .

Следовательно

.

Таким образом, периодическое решение, полученное в примере 1 устойчиво.

Интересно провести сравнение исследования систем с помощью приближенного метода гармонической линеаризации и точных методов исследования - фазовой плоскости и припасовывания. Приведем результаты моделирования в MATHCAD 7 нелинейной системы, рассмотренной в примере 1.

Как видно из Рис.10 фазовые траектории образуют устойчивый предельный цикл

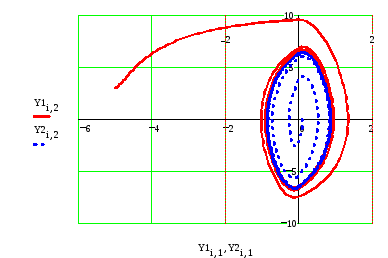
Рис.10.

Амплитуду и частоту автоколебаний можно найти из переходного процесса

Рис.11.

Амплитуда колебаний в и частота , что говорит о практическом совпадении результатов, так как в и .

Рассмотрим пример 3 исследования нелинейной САУ с помощью метода гармонической линеаризации. Будем исследовать нелинейную систему Рис.4, если нелинейный элемент представляет собой чувствительный элемент, имеющий релейную характеристику с зоной нечувствительности. Линейная часть осталась без изменения.

Коэффициенты гармонической линеаризации при этом равны

,

.

Для нахождения периодического решения построим кривую Михайлова

,

при 1/сек, сек, сек, в и в.

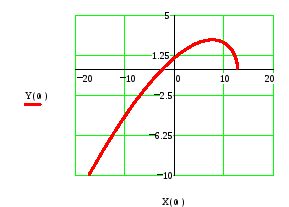
Рис.12.

Кривая Михайлова построена при значении амплитуды в, при которой она наиболее близко подходит к началу координат. Вместе с тем, не удается подобрать значение , при котором кривая Михайлова проходила бы через начало координат. Этот факт говорит о том, что при таких параметрах в системе не возможны автоколебания.

Рассматриваемая система имеет следующий вид фазовых траекторий и переходных процессов

Как видим, в исследуемой системе отсутствуют автоколебания.

Теперь рассмотрим частотный способ определения параметров автоколебаний. Для этого запишем частотную передаточную функцию разомкнутой системы

. (32)

Согласно критерию Найквиста в замкнутой системе возникнут колебания, если амплитудно-фазовая частотная характеристика разомкнутой системы пройдет через точку (-1, j0). Эти колебания будут устойчивыми, если при возрастании амплитуды на АФЧХ не будет охватывать точку (-1, j0), при этом колебания затухают и при АФЧХ будет охватывать точку (-1, j0), при этом колебания расходятся.

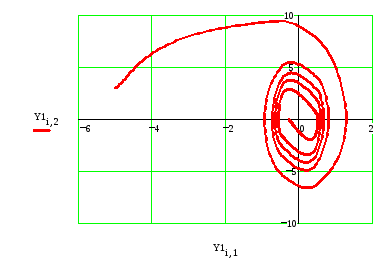
Рис.13.

Рис.14.

Решим задачу примера 1, определив параметры автоколебаний частотным способом. Запишем частотную передаточную функцию разомкнутой системы

.

АФЧХ разомкнутой системы проходит через точку с координатами

(-1, j0) при амплитуде в. Увеличенный фрагмент АФЧХ показан на Рис.15.

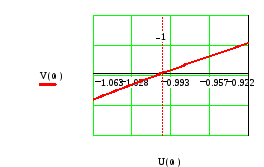
_Рис.15.

_{Частота колебаний определялась из условий}

_{, .}

_{Для значений частот}

_,

_{были получены следующие значения}

Откуда . Таким образом, результаты расчетов, выполненные двумя разными способами, практически совпадают. Давая различные по знаку приращения нетрудно показать, что полученные колебания устойчивые.

Возможен несколько иной подход к определению периодического решения. Запишем условие возникновения колебаний

, (33)

или

. (34)

Уравнение (34), позволяющее определить параметры колебаний в исследуемой системе решается графически. На комплексной плоскости строятся АФЧХ линейной части и обратная АФЧХ линеаризованной нелинейности с отрицательным знаком. Точка пересечения этих характеристик и определяет искомые частоту и амплитуду колебаний.

Полученное периодическое решение необходимо исследовать на устойчивость. В замкнутой системе возникнут колебания, если амплитудно-фазовая частотная характеристика разомкнутой системы пройдет через точку (-1, j0). Эти колебания будут устойчивыми, если при АФЧХ не будет охватывать точку (-1, j0) - колебания затухают, а при АФЧХ будет охватывать точку (-1, j0) - колебания расходятся.

Таким образом, в точке (-1, j0) при должно выполняться условие

,

или

. (35)

Из этого условия следует, что для устойчивости колебаний при увеличении кривая должно пересекать кривую изнутри вовне.

Определим параметры автоколебаний в системе Рис.4, если нелинейный элемент представляет собой чувствительный элемент, имеющий релейную характеристику с зоной нечувствительности и гистерезисом. Линейная часть осталась такой же, как и в примере 1.

Запишем коэффициенты гармонической линеаризации

,

.

В рассматриваемом случае уравнение (34) примет вид

.

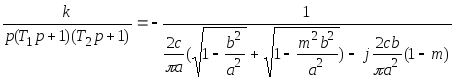Расчеты проводились при 1/сек, сек, сек, в, в и . На Рис.15 и Рис. 16 показаны фрагменты АФЧХ линейной части и отрицательной обратной АФЧХ нелинейной части в разном масштабе. Необходимо отметить, что характеристика нелинейной части образует петлю и дважды пересекается с характеристикой линейной части исследуемой системы. Таким образом, на возможность возникновения колебаний нужно исследовать две точки пересечения.

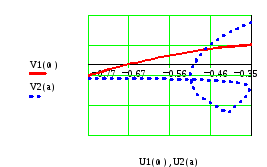
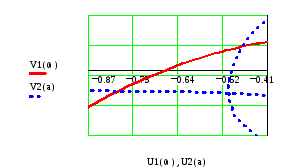
Рис.16. Рис.17.

_{Левая точка пересечения имеет координаты U1=-0,784 и V1=-0,0623. Найдем амплитуду колебаний, при которой кривая} наиболее близко проходит через точку с указанными координатами. Амплитуда принимает ряд значений _{, при этом координаты точек кривой} равны

_{Таким образом .}

_{Аналогично может быть определена амплитуда колебаний в правой точке пересечения U2=-0,473 и V2=0,072. Амплитуда принимает значения , при которых}

_{Следовательно .}

_{Частота колебаний для находится из условия прохождения кривой через точку U1=-0,784 и V1=-0,0623. Частота принимает ряд значений}

_{Наиболее близко кривая проходит через указанную точку при . Частота колебаний в правой точке .}

_{Проверка устойчивости полученных решений с помощью условия (35) показывает, что колебания в левой точке с амплитудой и частотой устойчивы, а в правой точке не устойчивы.}

_{Рассмотренную задачу проще решить с помощью построения АФЧХ разомкнутой системы (32) и применения критерия Найквиста. Увеличенный фрагмент АФЧХ при приведен на Рис.18.}

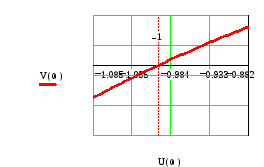
Рис.18.

Частота колебаний находится из условия выполнения равенства . Частота принимает значения _{. Для этих значений модуль равен}

_{Следовательно, искомая частота колебаний . Нетрудно убедиться, что возникшие колебания устойчивы.}

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Для нелинейной характеристики, вид которой соответствует номеру варианта, согласно таблице 1, рассчитать коэффициенты гармонической линеаризации.

2. Определить параметры автоколебаний для системы, представленной на рис. 4., при этом релейная характеристика нелинейного элемента, выбирается из таблицы 1, параметры системы – из таблицы 2, согласно номеру варианта.

2.1 Амплитуда и частота автоколебаний для исследуемой системы определяется алгебраическим способом.

2.2 Нахождение параметров автоколебаний с помощью критерия Михайлова.

2.3 Применение частотного способа.

3. Исследовать систему на устойчивость. В MATHCAD построить фазовый портрет, характеризующий поведение нелинейной системы. Построить переходные процессы для выходной координаты y(t). Исследовать влияние параметров САУ k и T на автоколебания.

Таблица 1.

Номер варианта	Вид нелинейной характеристики	Параметры звена
1 9 17 25	С зоной нечувствительности	b 0,1 0,3 0,2 0,4		c 1 2 1,5 3
2 10 18 26	С гистерезисной петлей	b 0,1 0,3 0,2 0,4		c 1 2 1,5 3
3 11 19 27	Идеальное звено	c 1 2 1,5 3
4 12 20 28	С зоной нечувствительности и насыщением	b 0,1 0,3 0,2 0,4	c 1 2 1,5 3		k 0,5 0,3 0,6 0,5
5 13 21	С зоной нечувствительности без насыщения	b 0,1 0,3 0,2	k 0,5 0,3 0,6
6 14 22	Без зоны нечувствительности, с насыщением	b 0,1 0,3 0,2	c 1 2 1,5
7 15 23	С переменным коэффициентом усиления	b 0,1 0,3 0,2	k1 0,5 0,3 0,6		k2 0,4 0,2 0,3
8 16 24	С насыщением и гистерезисной петлей	b 0,1 0,3 0,2	c 1 2 1,5		k 0,5 0,3 0,6

Таблица 2.

Номер варианта	k (1/сек)	T1 (сек)	T2 (сек)	Номер варианта	k (1/сек)	T1 (сек)	T2 (сек)
1	10	0,3	0,2	15	11	0,08	0,2
2	11	0,1	0,08	16	7	0,05	0,1
3	9	0,2	0,3	17	8	0,1	0,3
4	8	0,05	0,2	18	12	0,3	0,5
5	10	0,08	0,4	19	13	0,1	0,4
6	12	0,25	0,3	20	10	0,2	0,7
7	7	0,1	0,25	21	8	0,05	0,2
8	9	0,5	0,6	22	11	0,2	0,5
9	10	0,7	0,8	23	10	0,08	0,1
10	12	0,4	0,1	24	9	0,1	0,25
11	11	0,1	0,3	25	12	0,7	0,4
12	10	0,05	0,25	26	10	0,5	0,2
13	13	0,1	0,5	27	13	0,1	0,5
14	9	0,15	0,3	28	8	0,05	0,7

СОДРЕЖАНИЕ ОТЧЕТА

Отчет должен содержать:

- задание на лабораторную работу, ее цель и задачи;

- структурную схему системы, передаточные функции ее элементов, характеристику нелинейного элемента;

- программу в MATHCAD для нахождения параметров автоколебаний;

- фазовые портреты исследуемой нелинейной системы, переходные процессы;

- выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем особенности метода гармонической линеаризации, каковы его основные достоинства и недостатки.

2. Каким образом представляется выходной сигнал нелинейной части системы, при использовании метода гармонической линеаризации.

3. Какие частоты линейная часть нелинейной системы отфильтровывает, а какие пропускает без ослабления. Почему.

4. Назовите допущение, которое делается в методе гармонической линеаризации при описании сигнала на выходе линейной части.

5. Как рассчитать коэффициенты гармонической линеаризации.

6. Чем отличается линеаризация нелинейности в случае симметричных и несимметричных колебаний.

7. Какие существуют способы для определения параметров амплитуды и частоты автоколебаний линеаризованных систем.

8. В чем суть алгебраического способа.

9. Как с помощью критерия Михайлова исследовать линеаризованную систему на устойчивость.

10. В каком случае, согласно критерию Найквиста в замкнутой системе возникнут колебания.

Литература

1. Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления с примерами в системе MatLab. СПб.: Наука, 1999.

2. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. - М.: Наука, 1975.

3. Дьяконов В. MATLAB 6: Учебный курс. Питер. 2001.

4. Дьяконов В., Абраменкова И., Круглов В. MATLAB с пакетами расширений. Нолидж. 2001.

5. Сборник задач по теории автоматического регулирования и управления/ Под редакцией В. А. Бесекерского. - M.: Наука, 1978.

ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ РАБОТЫ

Подготовка к работе – 2,0 акад.часа

Выполнение работы – 1,0 акад.часа

Оформление работы – 1,0 акад.часа

21