лабораторная работа / Лаба№8 Метод частотных характеристик. Пример синтеза с продолжением

Международный университет природы, общества и человека «Дубна»

Кафедра «Персональная электроника»

Лабораторная работа №8

по дисциплине «Основы автоматических систем управления»

Метод частотных характеристик. Пример синтеза с продолжением: система чтения информации с диска.

Выполнил	Зернин Н.Д.
Принял	проф. Трофимов А.Т.

Дубна, 2010 г.

Цель работы:

• Рассмотреть метод частотных характеристик.

• Оценить показатели качества системы во временной области по ее частотным характеристикам.

• Применить метод частотных характеристик к синтезу системы чтения информации с диска.

Используемые средства: ИКС MATLAB.

Теоретическое введение.

Частотная характеристика определяется как реакция системы в установившемся режиме на синусоидальный входной сигнал при изменении его частоты во всем возможном диапазоне. При этом в линейной системе как входной сигнал, так и сигнал в любой другой точке в установившемся режиме являются синусоидальными; они отличаются от входного сигнала только по амплитуде и по фазе.

Рассмотрим выражение для выходного сигнала системы Y(s) = T(s)R(s) в случае, когда r(t)=Asinωt. Запишем

и

где все полюсы предполагаются различными. Тогда, раскладывая Y(s) на простые дроби, получим:

Обратное преобразование Лапласа от этого выражения даёт:

где и — константы. Если система устойчива, т. е. все p_i имеют отрицательные ненулевые действительные части, то

поскольку все экспоненциальные составляющие вида стремятся к нулю при .

В пределе при , т. е. в установившемся режиме, мы получим:

где .

Таким образом, выходной сигнал в установившемся режиме при определенном значении частоты зависит только от модуля и аргумента . Подчеркнём, что выражение справедливо только в случае, когда система является устойчивой.

Важным преимуществом метода частотных характеристик является то, что он может применяться при тестовых синусоидальных сигналах всех возможных частот и амплитуд. Так, например, легко могут быть экспериментально получены частотные характеристики системы, и это наиболее простой и надёжный способ анализа её свойств. По экспериментально полученным частотным характеристикам можно определить передаточную функцию системы. Кроме того, при синтезе системы в частотной области инженер получает ценную информацию о полосе пропускания системы и может оценить её реакцию на нежелательные шумы и возмущения.

Ещё одно преимущество метода частотных характеристик заключается в том, что поведение системы в установившемся режиме при синусоидальном входном сигнале можно описать путём замены в передаточной функции T(s). В результате мы получаем комплексную функцию , модуль и аргумент которой, будучи представлены графически, дают полезную информацию, необходимую для анализа и синтеза систем управления.

Недостаток метода частотных характеристик заключается в том, что отсутствует прямая связь между свойствами системы во временной и частотной областях. Такая связь прослеживается лишь частично, и на практике вид частотных характеристик обычно подбирается так, чтобы они в какой-то степени удовлетворяли требуемому поведению системы во временной области.

Введем прямое и обратное преобразование Фурье:

Преобразование Фурье существует для функций, удовлетворяющих условию:

С помощью преобразования Лапласа мы можем определить положение на s-плоскости полюсов и нулей передаточной функции Т(s), однако с помощью частотных характеристик, и конкретно с помощью функции , мы можем определить амплитудные и фазовые характеристики системы и тем самым получить сведения, полезные при анализе системы управления.

Если речь идет о частотных характеристиках замкнутой системы, то мы можем использовать преобразование Фурье входного сигнала r(t) в виде:

Тогда для одноконтурной системы управления выходной сигнал можно получить простой заменой в выражении Y(s)=T(s)R(s), т.е.

Применяя обратное преобразование Фурье, получим выражение для выходного сигнала:

Решение задачи существенно упрощается при использовании логарифмических частотных характеристик, часто называемых диаграммами Боде. Передаточные функции, нули которых расположены в правой полуплоскости, классифицируются как создающие неминимальный фазовый сдвиг. Передаточная функция, все нули которой расположены в левой полуплоскости, называется минимально-фазовой. В свою очередь, передаточная функция , удовлетворяющая условию , но все нули которой расположены в правой полуплоскости симметрично нулям относительно мнимой оси, называется неминимально-фазовой. Есть определенные требования к качеству системы: максимальное значение амплитудно-частотной характеристики, , имеет место на резонансной частоте ; полоса пропускания определяется частотой , на которой амплитудно-частотная характеристика системы уменьшается на 3 дБ относительно ее значения на низких частотах.

Рассмотрим систему второго порядка, которая в замкнутом состоянии имеет передаточную функцию:

Связь между резонансной частотой , максимумом амплитудно-частотной характеристики , коэффициентом затухания и собственной частотой приведена на рисунке 2.

zeta=[0.15:0.01:0.7];

wr_over_wn=sqrt(1-2*zeta.^2);

Mp=(2*zeta.*sqrt(1-zeta.^2)).^(-1);

subplot(121),plot(zeta,Mp),grid

xlabel('\zeta'),ylabel('M_{p\omega}')

subplot(122),plot(zeta,wr_over_wn),grid

xlabel('\zeta'), ylabel('\omega r/\omega n')

Рис. 2. График зависимостей и от параметра для системы второго порядка.

Рассмотрим систему управления гравировальной машиной. Необходимо выбрать значение K, обеспечивающее приемлемое качество реакции системы на ступенчатый входной сигнал. В качестве первого приближения выберем значение K=2, а затем, если качество системы окажется неприемлемым, будем решать задачу итерационным методом с помощью программы.

num=[K]; den=[1 3 2 K];

sys=tf(num,den);

w=logspace(-1,1.400);

[mag,phase,w]=bode(sys,w);

[mp,l]=max(mag); wr=w(l);

mp, wr

( Скрипт engrave1 )

>> K=2; engrave1

mp = 1.8178

wr = 0.8523

ts=4/zeta/wn

po=100*exp(-zeta*pi/sqrt(1-zeta^2))

( Скрипт engrave2 )

>> zeta=0.29; wn=0.88; engrave2

ts = 15.6740

po = 38.5979

По этой диаграмме Боде определяются показатели и , а затем соответствующие значения и . По полученным значениям оценивается время установления и относительное перерегулирование:

, перерегулирование .

Если эти параметры оказываются неприемлемыми, то необходимо изменить значение K и повторить процедуру. При K=2 мы получим следующие оценки: и , что позволяет предсказать ожидаемое значение перерегулирования в 38% и времени установления 15.67 с. Построим переходную характеристику.

K=2; num=[K]; den=[1 3 2 K];

sys=tf(num,den);

t=[0:0.01:20];

step(sys,t),grid

xlabel('Время (с)'),ylabel('y(t)')

Рис. 4. График переходной характеристики системы управления гравировальной машиной при K=2.

Переходная характеристика показывает, что предсказанные показатели качества очень хорошо совпадают с действительными, т.е. замкнутая система адекватно реагирует на входное воздействие.

Выводы:

1. Частотные характеристики систем управления представляют собой реакцию системы в установившемся режиме на синусоидальный входной сигнал.

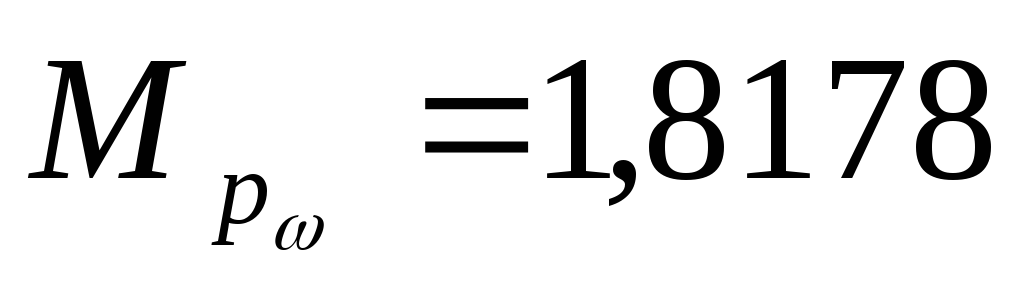2. Были рассмотрены некоторые параметры частотных характеристик, характеризующие качество системы; среди них важнейшими являются максимум амплитудной характеристики и резонансная частота . В рассмотренной нами системе управления гравировальной машиной мы нашли эти характеристики: и . По этим данным мы определили время установления (15,67 с.) и величину перерегулирования (38%).

3. Мы применили метод частотных характеристик к системе чтения информации с диска (рис. 5.). При известных значениях коэффициента затухания и собственной частоты мы нашли время установления (равное 0,7 мс.).

Система чтения информации с диска.

К модели двигателя и нагрузки добавим эффект гибкости пластины. Передаточная функция системы, состоящей из пружины и массы имеет вид:

.

Типичные параметры пластины и головки: и собственная резонансная частота Гц. Следовательно, . Построим амплитудные характеристики диаграммы Боде для замкнутой системы:

K=100; num=[K K];

den=[0.00000000000056 0.0000000064 0.000204 0.204 4 0];

sys=tf(num,den);

bode(sys)

Рис. 5. График диаграммы Боде, соответствующий G(s).

Оценим время установления с помощью выражения:

,

что составляет 0,7 мс. И пока выполняется условие , резонанс, свойственный упругой пластине с головкой, находится вне полосы пропускания системы.

Выводы:

4. Частотные характеристики систем управления представляют собой реакцию системы в установившемся режиме на синусоидальный входной сигнал.

5. Были рассмотрены некоторые параметры частотных характеристик, характеризующие качество системы; среди них важнейшими являются максимум амплитудной характеристики и резонансная частота . В рассмотренной нами системе управления гравировальной машиной мы нашли эти характеристики: и . По этим данным мы определили время установления (15,67 с.) и величину перерегулирования (38%).

6. Мы применили метод частотных характеристик к системе чтения информации с диска (рис. 5.). При известных значениях коэффициента затухания и собственной частоты мы нашли время установления (равное 0,7 мс.).

0