44. Производная обратной функции

Дифференцируемая монотонная функция f: ]a, b[ → R с необращающейся в нуль производной имеет обратную дифференцируемую функцию f -1, производная которой вычисляется по формуле Доказательство. Считаем f строго монотонно возрастающей, тогда f -1(y) непрерывна, монотонно возрастает на [f(a),f(b)]. Положим y0=f(x0), y=f(x), x - x0=Dx, y - y0=Dy. В силу непрерывности функции Dy®0 Þ Dx®0, имеем. Переходя к пределу, получим требуемое равенство. Производная четной функции нечетна, производная нечетной функции четна. Действительно, если x® - x0 , то -x® x0, поэтому. Для четной функции, для нечетной функции.

45. Производная сложной функции

Теорема. Если существуют f¢(x0), g¢(x0) и x0=g(t0), то в некоторой окрестности t0 определена сложная функция f(g(t)), она дифференцируема в точке t0 иДоказательство. f(x) - f(x0)=f¢(x0)(x-x0)+a(x)(x-x0), xÎU(x0). Можно считать a(x0)=0. f(g(t))- f(g(t0))= f¢(x0)( g(t)- g(t0))+a( g(t))( g(t)- g(t0)) Поделим обе части этого равенства на (t - t0) и перейдем к пределу при t®t0.

46. Производная неявной функции

При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение. Отсюда получим формулу для производной функции заданной неявно: Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением:

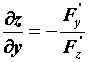
47. Понятие о производных и дифференциалах высшего порядка

Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом, f"(x) = (f'(x))'.Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак, f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x).Число n называется порядком производной.

Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом, dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N. Если x - независимая переменная, то dx = const и d2x = d3x = ... = dnx = 0. В этом случае справедлива формула dnf(x) = f(n)(x)(dx)n.

Если функции u = f(x) и v = g(x) дифференцируемы, то

1) (Сu)(n) = Cu(n);

2) (u ± v)(n) = u(n) ± v(n);

3) Это выражение называется формулой Лейбница. Также по формуле dny = f(n)(x)dxn может быть найден дифференциал n- го порядка.

48. Теоремы о среднем для дифференцируемых функций

Теорема 10.2. (Ролль). Пусть функция f:

1. непрерывна на отрезке [a,b];

2. имеет в каждой точке интервала (a,b) производную;

3. f(a) = f(b).

Тогда существует точка x такая, что f/(x) = 0, a < x < b.

Д о к а з а т е л ь с т в о:

П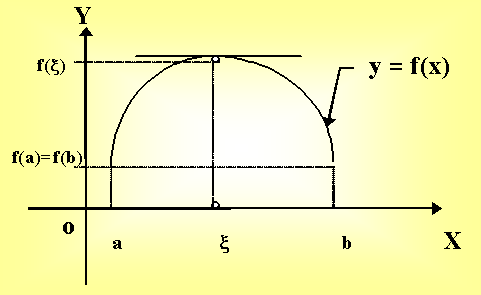усть f непрерывная на [a,b] принимает на этом отрезке наибольшее и наименьшее значения в некоторых точках этого отрезка. Обозначим М = max f(x), m = min f(x) тогда для всех x Î [a,b] справедливо m £ f(x) £ M. Если m = M Þ f - const и, следовательно, f/ º 0. Если m ¹ M Þ из условия f(a) = f(b) следует, что хоть одно из значений m или M не принимается на концах [a,b]. Пусть, например, это будет точка М, т.е. существует xÎ (a,b), что f(x) = М. Тогда из теоремы 10.1 следует, что f/ = 0. Геометрически теорема Ролля означает, что если выполнены условия теоремы, то существует точка, в которой касательная параллельна оси абсцисс.

Другая формулировка теоремы Ролля.

Между двумя последовательными корнями дифференцируемой функции всегда содержится по крайней мере один корень ее производной.

З а м е ч а н и е. Все три условия теоремы существенны.

Если не выполняется одно из условий, то не существует такой точки xÎ (a,b), что f/(x) = 0.

Теорема 10.3. (Лагранж). Пусть f непрерывна на [a,b] и имеет производную в каждой точке интервала (a,b). Тогда существует такая точка x ,что:

f(b) - f(a) = f/(x)(b-a) , a<x<b (10.3)

Д о к а з а т е л ь с т в о: Рассмотрим вспомогательную функцию

F(x) = f(x) - lx, (10.4)

где число l выберем таким образом, чтобы F(a) = F(b), т.е. чтобы f(a) - la = f(b) - lb. Для этого достаточно взять Тогда для F(x) выполнены условия теоремы Ролля: F(x) - непрерывна на [a,b], дифференцируема на (a,b) и принимает на концах одинаковые значения, поэтому существует такая точка x Î (a,b), что F/(x) = 0. Тогда из (10.4) получаем F/(х) = f/(х)-l, поэтому f/(x) - l=0 и из (10.5) получим. Геометрический смысл теоремы Лагранжа состоит в следующем. Пусть А(а,f(а)), В(b,f(b)) - точки графика функции f, АВ - хорда, соединяющая точки А и В. Тогда отношениеТ.е. в условиях теоремы можно сказать, что найдется точка, возможно не одна, в которой касательная к графику параллельна хорде .

З а м е ч а н и е. Теорема Лагранжа найдет ряд важнейших приложений в дальнейшем.Запишем другую форму (10.6)

f(a) - f(b) = f/(x) (a-b) (10.7)

т.е. она справедлива для a>b и b>a.

Следствие 1. Если f/(х) = 0 " х Î (a,b) Þ f(х) = С - const.

Д о к а з а т е л ь с т в о: Пусть f/(х) = 0 при х Î (a,b) тогда для любого х Î (a,b) f(х) - f(b) = 0×(х-b). Следовательно f(х) = f(b)= const.

Следствие 2. Если f(х), g(x) - дифференцируемые на (a,b) и (в этих точках)

f/(х) = g/(x) " х Î (a,b) , а на концах промежутка, если они входят в область определения, - непрерывны, то эти функции отличаются на С - Сonst: f(х) - g(x) = С.

Д о к а з а т е л ь с т в о: Пусть f/(х) = g/(x) при х Î <a,b>, тогда на этом промежутке êf(х) - g(x)ê/ = f/(х) - g/(x) = 0. В силу следствия 1 имеем F/(х) = 0 Þ F(x) = С, а здесь F(х) = f(х) - g(x) = С.

Д о к а з а т е л ь с т в о:

Пусть для определенности f в точке x принимает наибольшее значение, т.е. f(x)£f(x) для всех xÎ (a,b), тогда, если x<x если x<x . Если существует производная , то в пределе при х® x-0 из (10.1) получим, что f/(x)³0, а из (10.2) при х® x+0 Þ f/(x)£0, что возможно лишь в случае f/(x)=0.

Г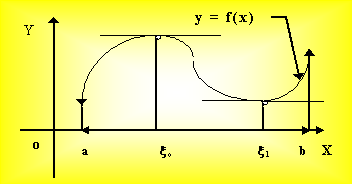еометрическая интерпретация теоремы Ферма состоит в том, что если в точке xÎ (a,b) функция f принимает наибольшее или наименьшее значение, то касательная в точке (x,f(x)) к графику функции параллельна оси Ох.