40. Достаточные условия дифференцируемости функции.

До к а з а т е л ь с т в о: (необходимость).Пусть f дифференцируема в точке x0 , т.е.

Dy = A Dх+ О(Dх) тогда=А+ =А Поэтому производная f/(x0) существует и равна А. Отсюда dy=f/(x0) dx.

(достаточность) Пусть существует производная, т.е. существует = f/(x0) + e(Dх) , где И тогда " Dx ¹ 0 Dy= f/(x0) + e(Dх)×Dх (6.5)

И так как e(Dх)×Dх=О(Dх), то наличие равенства (6.5) означает дифференцируемость.

Из доказанного следует, что А - коэффициент в определении дифференциала - определен однозначно. Из формулы (6.5) получаем новое обозначение для производной у/ =.

Примеры :

dС = 0, (С - Сonst);

dSin(x) = Cos(x)dx;

dCos(x) = -Sin(x)dx;

dax=ax lna dx, (dex=ex dx );

dxn=n xn-1 dx, ( n - положительное число ).

41. Геометрический смысл производной

Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Рассмотрим график функции y = f ( x ):

Из рис.1 видно, что для любых двух точек A и B графика функции: xf(x0+x)−f(x0)/=tgа, где а - угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

42.Геометрический смысл дифференциала

Выясним геометрический смысл дифференциала. Для этого проведем к графику функции у=ƒ(х) в точке М(х; у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке ½ АМ½ =∆х, |AM1|=∆у. Из прямоугольного треугольника МАВ имеем: Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х. Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

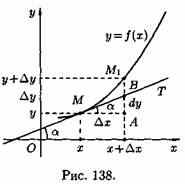
В этом и состоит геометрический смысл дифференциала.

43. Основные правила дифференцирования

Основные правила дифференцирования.

Если функции f и g дифференцируемы в точке то в этой же точке дифференцируемы сумма, произведение и частное (если ) этих функций, причем .

Доказательство: а) По свойству предела суммы получаемПостоянный множитель C можно выносить из-под знака производной: В частности,

Б) Функцию f · g можно записать в видеНо По свойству предела произведения получаемИспользуя доказанное равенство, получим, чтоРаскрывая скобки и приводя подобные члены, получим формулу

в) Для доказательства этой формулы заметим, что Воспользовавшись свойством предела частного, получимПосле этого представим как произведение функций f иоткуда и следует доказываемая формула. Если f дифференцируема, то где также дифференцируема, причем