32. Доказать свойства пределов функции
Теорема 1.
Предел алгебраической суммы двух, трех
и вообще определенного числа функций
равен алгебраической сумме пределов
этих функций, т.е.
.
Доказательство.
Проведем доказательство для двух
слагаемых, так как для любого числа
слагаемых оно проводится так же. Пусть
.
Тогда f(x)=b+α(x) и g(x)=c+β(x), где α и β –
бесконечно малые функции. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)). Так как b + c есть
постоянная величина, а α(x) + β(x) – функция
бесконечно малая, то
.
Пример:
.
Теорема 2.
Предел произведения двух, трех и вообще
конечного числа функций равен произведению
пределов этих функций:
.
Доказательство.
Пусть
.
Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и fg = (b +
α)(c + β) = bc + (bβ + cα + αβ). Произведение bc
есть величина постоянная. Функция bβ +
c α + αβ на основании свойств бесконечно
малых функций есть величина бесконечно
малая. Поэтому
.
Следствие 1.
Постоянный множитель можно выносить
за знак предела:
.
Следствие 2.
Предел степени равен степени предела:
.
Пример:
.
Теорема
3. Предел
частного двух функций равен частному
пределов этих функций, если предел
знаменателя отличен от нуля, т.е.
.
Доказательство.
Пусть
.
Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α,
β – бесконечно малые. Рассмотрим
частное
.
Дробь
является бесконечно малой функцией,
так как числитель есть бесконечно малая
функция, а знаменатель имеет предел
c2≠0.
Пример:
.
33. Первый замечательный предел и его следствия
Теорема.(Первый
замечательный предел).
Предел отношения синуса бесконечно
малой дуги к самой дуге, выраженной в
радианах, равен единице,
.
Д о к а з а т е л ь с т в о:
Пусть х > 0 и х
® 0, так что 0 < х <
.
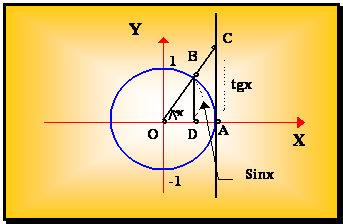В тригонометрическом
круге R = 1 рассмотрим S DОАВ,
S cек. ОАВ, SDОАВ
SDОАВ =
SDОАВ
=
Получаем
т.е. Sin x < x < tg x разделим на Sin x > 0, получим
1 <
или cos x <
.
Пусть теперь х ® 0 + 0, но
т.к.
1 - cos x = 2 sin2
бесконечно
малая по условию, то
.
Тогда функция
заключена
между двумя функциями, имеющими предел,
равный 1. На основании свойства 1, получаем
.
Если х < 0 ; имеем
.
где - х > 0. Поэтому
.
З а м е ч а н и е. " х çsin x ç £ çx ç,
причем равенство имеет место при х =
0.
34. Непрерывность функции в точке.
Пусть функция у=ƒ(х)
определена в точке хо и в некоторой
окрестности этой точки. Функция y=f(x)
называется непрерывной
в точке х0,
если существует предел функции в этой
точке и он равен значению функции в этой
точке, т. е.
Равенство (19.1) означает выполнение трех условий:
1) функция ƒ (х) определена в точке x0 и в ее окрестности;
2) функция ƒ(х) имеет предел при х→хо;
3) предел функции в точке хо равен значению функции в этой точке, т. е. выполняется равенство (19.1).
Так как
то равенство (19.1) можно записать в виде
.
Это означает, что при нахождении предела
непрерывной функции ƒ(х) можно перейти
к пределу под знаком функции, то есть β
функцию ƒ(х) вместо аргумента х подставить
его предельное значение хо. Например:
В
первом равенстве функция и предел
поменялись местами (см. (19.2)) в силу
непрерывности функции еx .
Если f(x0-0)=f(x0+0), то х
называется точкой
устранимого разрыва.
Если доопределить функцию таким образом,
что f(x0)=
=
, то получим непрерывную функцию. Точка
разрыва, не являющаяся точкой разрыва
первого рода, называется точкой
разрыва второго рода.
Таким образом, в точках второго рода по
крайней мере один из пределов не
существует
,
.