Пример 1

Пусть звено описывается дифференциальным уравнением

T₂+T₁+y(t)=kx(t).

В операторной форме уравнение имеет вид

Y(p)(T₂p²+T₁p+1)=kX(p).

Откуда передаточная функция звена

W(p)==.

Пример 2

Решим обратную задачу - найдем по передаточной функции дифференциальное уравнение.

Пусть передаточная функция имеет вид:

W(p)==,

откуда

Y(p)(Tp+1)=kX(p);

TpY(p)+Y(p)=kX(p).

Учитывая, что p (формальное операционное соответствие), получим:

T+y(t)=kх(t).

Характеристическое уравнение звена

Многочлен в знаменателе передаточной функции звена A_n(p) называют характеристическим полиномом.

Характеристическое уравнение звена имеет вид A_n(p)=0, или A_npⁿ+A_n-1p^n-1+...+A₁p+1=0,

так что корни p_i характеристического уравнения звена являются полюсами его передаточной функции.

Виды типовых воздействий в САУ

При анализе работы систем автоматического регулирования и их отдельных элементов в качестве типовых выбирают одно из следующих возмущений.

Ступенчатое возмущение — мгновенное изменение воздействия на постоянную величину, чаще всего равную единице (рисунок 3, а). Физическая система испытывает толчок. Аналитически ступенчатое возмущение записывается в виде

f(t)=.

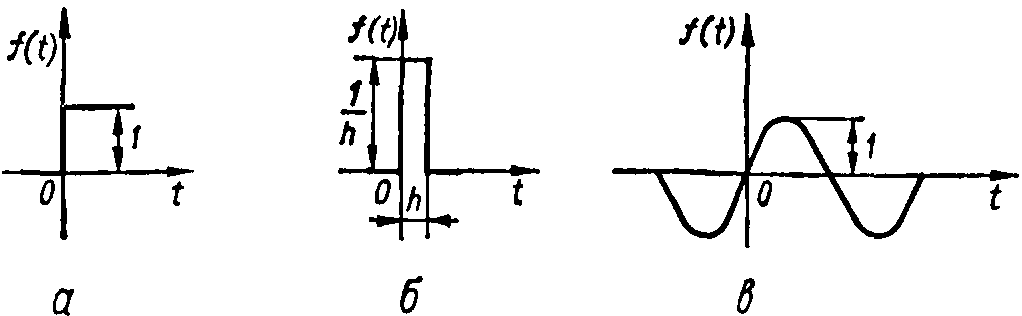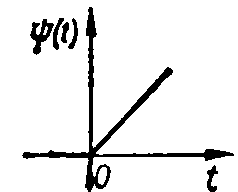г д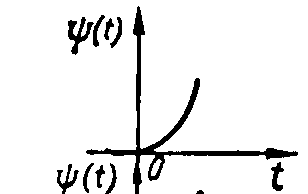

Рисунок 3 - Типовые возмущения систем: а — ступенчатое; б — импульсное; в — гармоническое; г — скачок скорости; д — скачок ускорения

Импульсное возмущение — возмущение, полученное как последовательность двух одинаковых по величине, но противоположных по знаку ступенчатых возмущений, сдвинутых во времени на величину, обратную величине их интенсивности (рисунок 3, б). Особое значение имеет единичная импульсная функция или дельта-функция, обозначаемая (t).

Дельта-функция обладает следующими свойствами:

(t)=,

.

Первое свойство означает, что дельта-функция существует лишь в момент времени t=0. Второе свойство означает, что, несмотря на пренебрежимо малую длительность функции, площадь, ограниченная ею, имеет конечное значение, равное единице. Единичная импульсная функция является производной от единичного скачка, т. е.:

(t)=.

Периодическое возмущение — возмущение, изменяющееся периодически во времени. Оно удобно для исследования автоматических систем, работающих в режиме незатухающих колебаний. Наиболее простым периодическим возмущением является гармоническое колебание единичной амплитуды (рисунок 3, в).

Скачок скорости или скачок ускорения — возмущения, являющиеся стандартными для следящих систем, которые работают в режиме постоянной скорости x(t)=at (рисунок 3, г) или постоянного ускорения x(t)=bt² (рисунок 3, д).

Переходная функция звена

Переходной функцией h(t) называется реакция звена на единичное ступенчатое воздействие (рисунок 4), т. е. переходный процесс на выходе y(t) при единичном скачке 1(t) на входе звена x(t)=1(t).

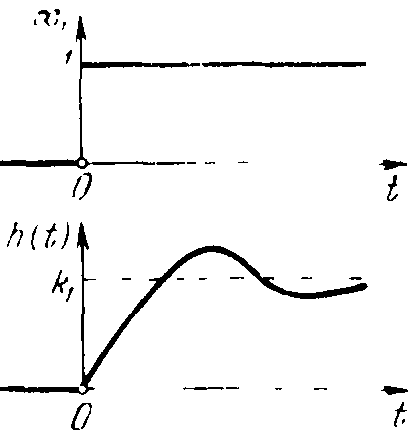
Рисунок 4 – Входное воздействие x(t)=1(t) и переходная функция звена h(t)

Переходная функция может быть определена экспериментально или вычислена теоретически.

Если на вход подается единичный скачок 1(t), то его изображение по Лапласу X(р)=L{1(t)}=. Зная передаточную функцию звена, W(p)=, находим изображение выходной величины как:

Y(p)=W(p)=.

Переходя к оригиналу, получим

h(t)==.

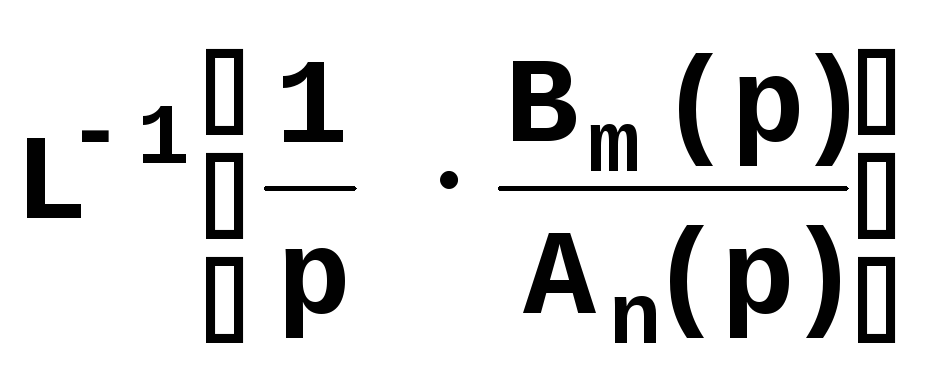Переход от изображения к оригиналу может быть осуществлен по таблице операционных соответствий или по теореме разложения

h(t)=+,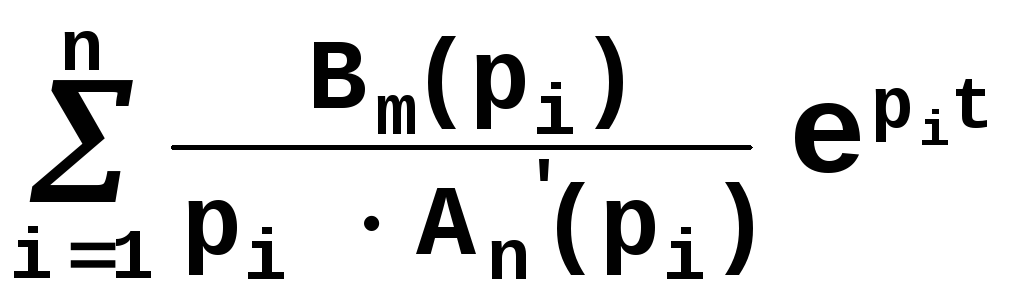

где p_i - корни характеристического уравнения A_npⁿ+A_n-1p^n-1+...+A₁p+1=0;

A^'(p_i) – производная A^'(p)= при p=p_i.

Для примера найдем переходную характеристику звена c передаточной функцией

W(p)=.

Характеристическое уравнение звена

Тp+1=0.

Корень p₁=-. Тогда по формуле обратного преобразования

h(t)=k.

Установившееся значение реакции на выходе элемента может быть легко определено из выражения

.

Для переходной характеристики h_уст=.

Частотные характеристики звена

Частотными характеристиками называются формулы и графики, характеризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме, то есть вынужденные синусоидальные колебания звена.

Если на вход звена подается единичный синусоидальный сигнал (как показано на рисунке 5)

x(t)=sint,

то на выходе будет (в установившемся режиме)

y(t)=Asin(t+),

где A — амплитуда (точнее, усиление амплитуды), а  — фаза (точнее, сдвиг по фазе).

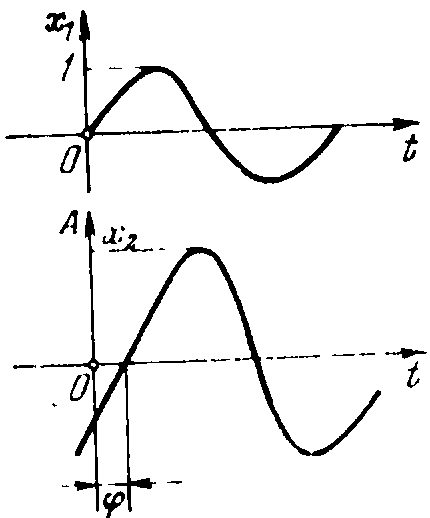
Рисунок 5 Реакция устойчивого звена на синусоидальное воздействие

Амплитудно-частотная характеристика (АЧХ) A() есть зависимость отношения амплитуды колебаний на выходе звена к амплитуде на входе от частоты входного сигнала:

A()=,

где A_вых(), A_вх - соответственно амплитуды выходного и входного сигналов;

 - частота входного сигнала.

Фазо-частотная характеристика (ФЧХ) () есть зависимость разности фаз выходного и входного сигналов от частоты входного сигнала

()=₂-₁,

где ₂, ₁ - начальные фазы соответственно выходного и входного сигналов.

Графики амплитудной и фазовой частотных характеристик изображаются графически (рисунок 6).

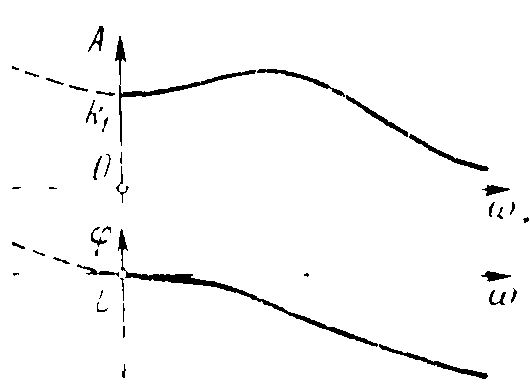
Рисунок 6 - Графики амплитудной и фазовой частотных характеристик

Амплитудно-фазовая характеристика (АФХ) есть отношение выходного и входного гармонического сигналов, записанных в комплексной форме, при изменении частоты входного сигнала от нуля до бесконечности.

АФХ изображается на комплексной плоскости и для каждой частоты представляет собой вектор длиной A(), идущий под углом () к вещественной положительной полуоси. Годограф, соединяющий концы векторов, построенных для всех частот от нуля и до бесконечности, и будет являться АФХ.

Амплитудно-фазовая частотная характеристика АФЧХ (ее еще называют комплексной передаточной функцией) звена получается из передаточной функции W(p) подстановкой p=j W(j)=W(р)_р=j.

W(j)=k.

Амплитудно-фазовая характеристика представляет собой комплексное число и может быть представлена в виде

W(j)=A()=U()+jV(),

где A()= – амплитудно-частотная характеристика;

U() - вещественная частотная характеристика;

V() - мнимая частотная характеристика.

Если передаточная функция представлена в виде отношения полиномов числителя и знаменателя, то модуль амплитудно-фазовой характеристики удобно находить как отношение модулей числителя и знаменателя:

A()=k,

а фазу - как разность аргументов числителя и знаменателя

()=arg[B_m(j)]-arg[А_n(j)].

Графически амплитудно-фазовая частотная характеристика изображается на комплексной плоскости (рисунок 7) в координатах (U, V), как годограф функции W(j). Можно строить амплитудно-фазовую частотную характеристику, выделив в выражении W(j) вещественную и мнимую части. При этом частоту  изменяют от 0 до  (сплошная кривая на рисунке 7) или же от — до +, когда добавляется еще симметричная к ней пунктирная кривая.

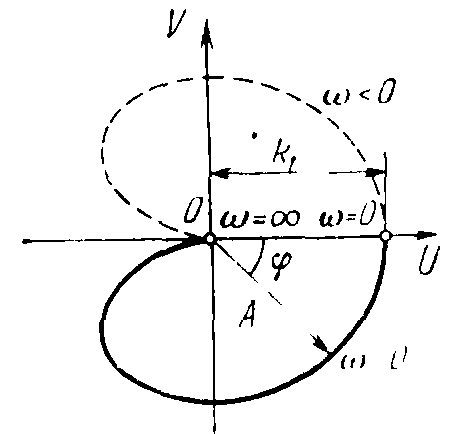
Рисунок 7 – АФЧХ звена

Логарифмические частотные характеристики

Чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе. Такие логарифмические частотные характеристики очень удобны для инженерных расчетов.

При построении логарифмической амплитудной частотной характеристики (ЛАЧХ) по оси ординат откладывают величину

L()=20lgA()=20lgW(j),

единицей измерения для которой является децибел (дБ). По оси абсцисс откладывается частота  в логарифмическом масштабе (рисунок 8).

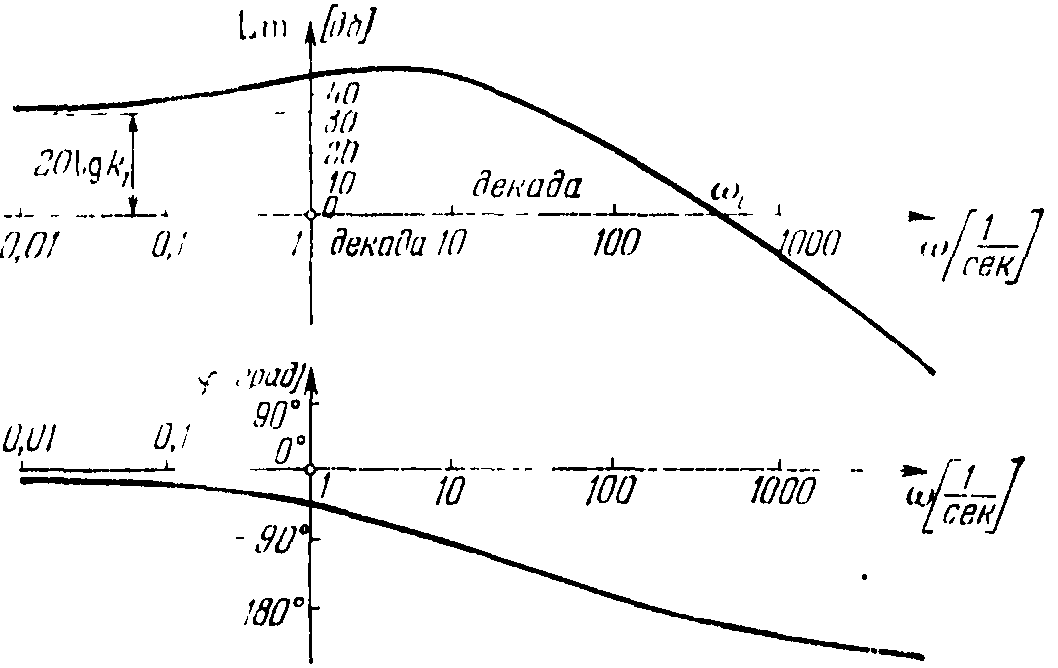
Рисунок 8 – Логарифмические частотные характеристики

Равномерной единицей на оси абсцисс является декада — любой отрезок, на котором значение частоты увеличивается в десять раз. Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза _ср.

Начало координат обычно помещают в точке =1, так как lg1=0. Точка же =0 лежит в —. Однако, в зависимости от интересующего нас диапазона частот можно начало координат брать и в другой точке (=0,1; =10 или др.)

При построении логарифмической фазовой частотной характеристики (ЛФХ) отсчет углов  идет по оси ординат в обычном масштабе в угловых градусах. По оси абсцисс частота  откладывается по-прежнему в логарифмическом масштабе.

Важно иметь в виду, что ось абсцисс (L=0) соответствует значению А=1, т. е. прохождению амплитуды сигнала через звено без изменения амплитуды. Верхняя полуплоскость ЛАЧХ соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость — значениям А<1 (ослабление амплитуды).

Основные типы звеньев

Типы звеньев систем автоматического управления и регулирования различаются в зависимости от вида их передаточных функций (или дифференциальных уравнений), определяющих их динамические свойства и характеристики.

Типовые динамические звенья характеризуются дифференциальными уравнениями, порядок которых не выше второго.

В зависимости от вида дифференциальных уравнений в теории автоматического управления различают следующие основные типовые звенья:

-безинерционное (пропорциональное или усилительное);

-инерционное первого порядка (или апериодическое);

-инерционное второго порядка;

-интегрирующее;

-дифференцирующее;

-реальное дифференцирующее;

-колебательное;

-звено запаздывания.

Основные типы звеньев делятся на три группы:

-позиционные;

-дифференцирующие;

-и интегрирующие.

Позиционными звеньями называются такие, в передаточной функции которых

W(р)=k=,

многочлены B_m(p) и A_n(p) имеют свободные члены равные 1, т. о. эти звенья обладают статической характеристикой y_уст=kx_уст (при р=0 W(р)=k=), определяющей их состояние равновесия - свойство позиционности.

У дифференцирующих звеньев в выражении передаточной функции отсутствует свободный член числителя, т. е. для однократно дифференцирующего звена будет b₀=0:

W(р)==

==kр,

где B_m-1(p) имеет свободный член, равный 1, а k= – коэффициент усиления.

Передаточные функции интегрирующих звеньев имеют соответственно вид:

W(р)==

==,

где A_n-1(p) имеет свободный член, равный 1.

Для двукратно интегрирующего звена a₀=a₁=0

W(р)==

==,

Знание характеристик типовых звеньев необходимо для расчетов систем управления.

Идеальное усилительное (безинерционное) звено

Уравнение и передаточная функция звена:

y(t)=kx(t), W(p)=k.

Примерами безинерционного звена являются редуктор, делитель напряжения, датчики угла, безинерционный усилитель и др. (рисунок 9).

Рисунок 9 - Примеры безинерционных звеньев

В действительности безинерционных звеньев нет. Обычно в САР идеальными считают звенья, инерционность которых значительно меньше инерционности других звеньев. Чаще всего это различные датчики и предварительные усилители. Инерционное запаздывание многих измерительных элементов автоматических систем (датчиков угла рассогласования, фотоэлектрических датчиков, магнитоэлектрических датчиков) мало, поэтому их считают безинерционными звеньями.

Амплитудно-фазовая частотная характеристика (рисунок 10):

W(j)=k; A()=k; ()=0.

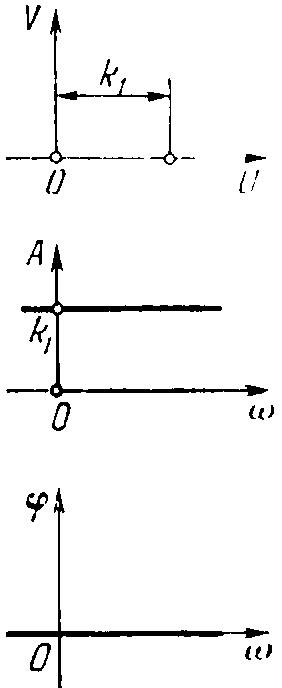
Рисунок 10 – Частотные характеристики безынерционного звена

Переходная функция звена:

h(t)=k, t>0.

Инерционное (апериодическое) звено

Уравнение и передаточная функция звена:

(Тр+1)Y(p)=kX(p); W(p)=,

где Т – постоянная времени;

k – коэффициент передачи звена.

Примерами инерционных (апериодических) звеньев являются двигатели постоянного тока, если х(t) — напряжение питания, а y(t) — угловая скорость вала (t); двухфазные асинхронные двигатели; усилители при учете инерционного запаздывания; массивное тело, если входной величиной считать количество поступающего в единицу времени тепла Q, а выходной — температуру в какой-либо точке внутри тела и др.); L-R цепочка (рисунок 11).

Рисунок 11 – Пример инерционного звена

Амплитудно-фазовая частотная характеристика:

W(j)= показана на рисунке 12.

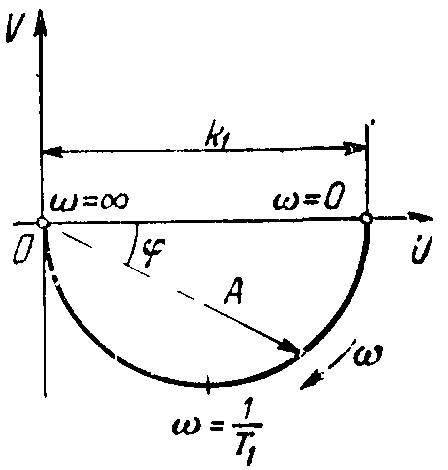
Рисунок 12 - Амплитудно-фазовая частотная характеристика инерционного звена

Из W(j) находим

A()=, ()=-arctgT.

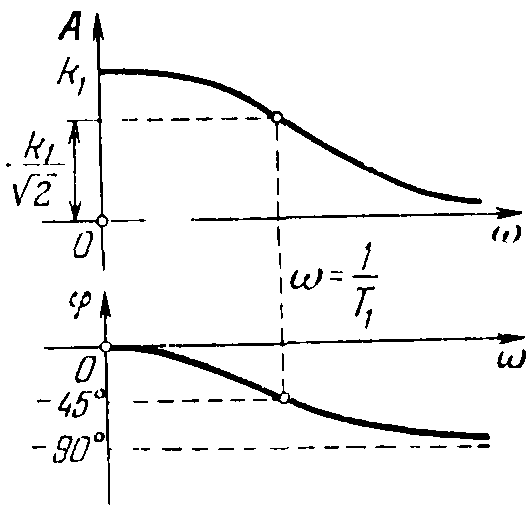
Рисунок 13 – Амплитудно-частотная и фазо-частотная характеристики инерционного звена

Логарифмическая амплитудно-частотная характеристика имеет вид:

L()=20lg=20lgk-20lg.

Эта характеристика имеет асимптоты:

а)при 0 L()20lgk;

б)при  L()20lgk-20lgT.

Последняя асимптота будет наклонной прямой с наклоном -20 дБ/дек, а первая – горизонтальная прямая. Пересекаются асимптоты в точке _с=. Сама ЛАЧХ близка к этим асимптотам.

На логарифмической сетке по оси частот откладывается сопрягающая частоте _с= (см. рисунок 14). Для частот меньших, чем сопрягающая, т. е. при <, можно пренебречь вторым слагаемым под корнем, тогда левее сопрягающей частоты можно заменить L() приближенным выражением

L()20lgk.

Этому выражению соответствует горизонтальная прямая. Для частот больших сопрягающей > в выражении для L() можно пренебречь 1 под корнем. Тогда L()=20lgk-20lg(T). Второе слагаемое представляет собой прямую линию, идущую под наклоном -20 дБ/дек. Ломаная линия и называется асимптотической ЛАЧХ. Наибольшее отклонение точной ЛАЧХ от асимптотической приблизительно равно 3 дБ на частоте сопряжения, т. к.:

L()=20lgk-20lg=20lgk-3,03 (дБ).

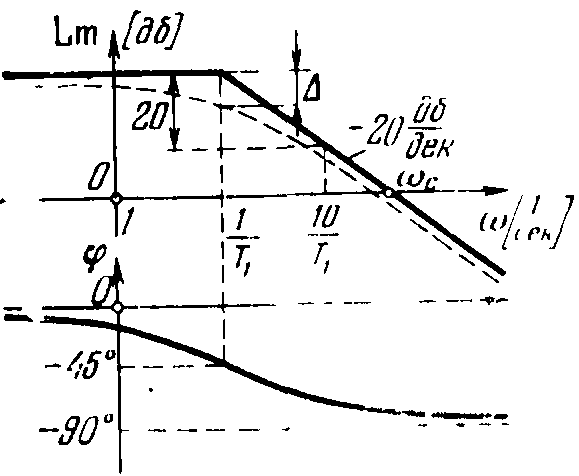
Рисунок 14 – ЛАЧХ инерционного звена

Переходная функция, согласно решению уравнения звена, при х(t)=1(t) и нулевых начальных условиях имеет вид:

h(t)=k.

Она изображена на рисунке 15.

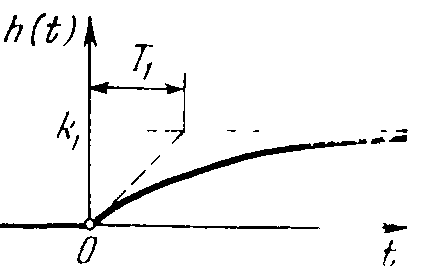
Рисунок 15 - Переходная функция инерционного звена

Постоянная времени Т определяет наклон касательной в начале кривой (рисунок 15). Следовательно, величина Т характеризует степень инерционности звена, т. е. длительности переходного процесса. Теоретически такой переходный процесс длится бесконечно долго. Практически для этого звена под временем переходного процесса понимают промежуток времени t_п по истечении которого выполняется неравенство:

1-h(t_п),

где  - наперед заданное положительное число (обычно =0,010,05).

При подаче на вход звена постоянного сигнала x₀ по окончании переходного процесса координата y(t) жестко связана с входной:

y_уст=y()=kx₀.

Колебательное звено

Уравнение и передаточная функция звена:

(T₂²p²+T₁p+1)Y(p)=kX(p), W(p)=,

причем предполагается T₁<2Т₂, так что корни характеристического уравнения T₂²p²+T₁p+1=0 — комплексные.

Общепринята запись передаточной функции колебательного звена в виде:

W(p)=,

где Т=T₂, = причем 0<<1, так как T₁<2Т₂. При 1 звено становится инерционным звеном второго порядка.

Амплитудно-фазовая частотная характеристика (рисунок 16) звена:

W(j)=,

A()=,

()=-arctg.

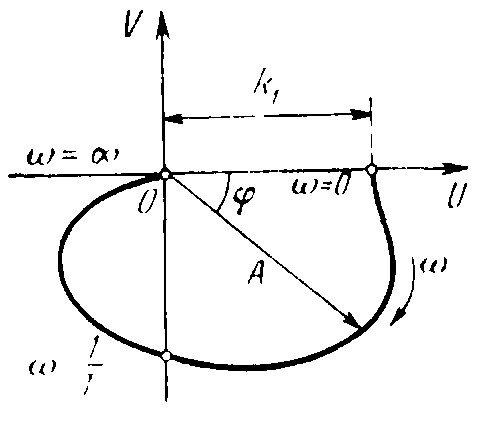
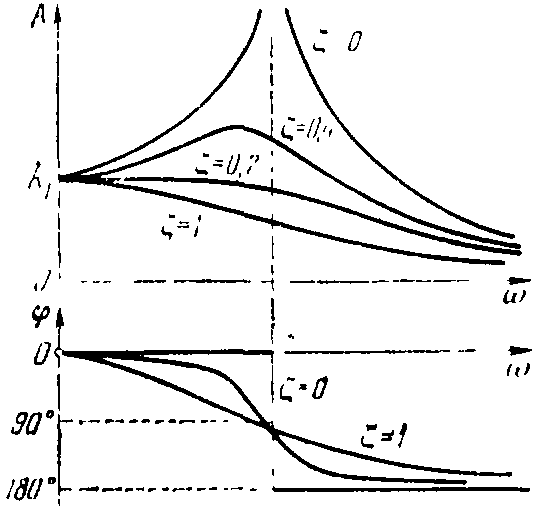
Рисунок 16 – Частотные характеристики колебательного звена

Амплитудная характеристика уменьшается с увеличением , т. е. А()k, если 1>>0,707. При <0,707 появляется максимум на характеристике А(), который уходит в бесконечность при 0. Поэтому величина = называется параметром затухания. Отсюда видна роль постоянных времени Т₁ и Т₂ в уравнении звена: постоянная Т₂ увеличивает колебания, а T₁ — демпфирует их.

Логарифмическая амплитудная частотная характеристика звена

L()=20lgk-20lg.

При значениях 0,5<<1 характеристика близка к ломаной (рисунок 17).

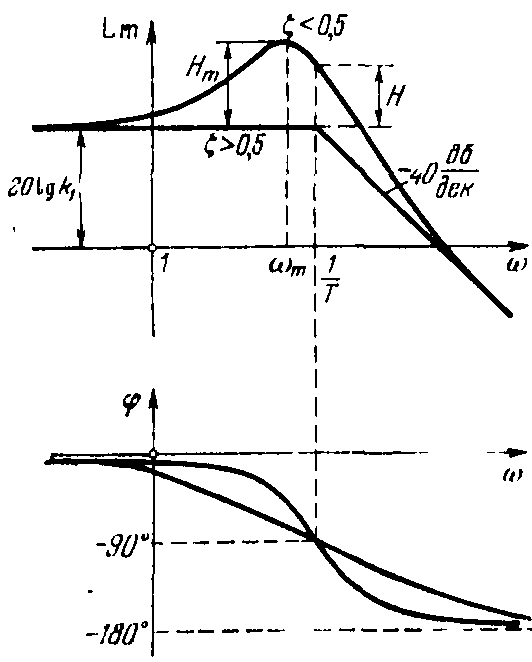
Рисунок 17 – Логарифмические частотные характеристики колебательного звена

Если же <0,5, то получается заметный максимум (рисунок 17). Тут необходимо вычислять превышение H_m

H_m=20lg

на частоте

_m=.

Имеются шаблоны для вычерчивания этой кривой.

В упрощенных расчетах достаточно находить H_m приближенно (см. рисунок 17):

H_m20lg при =.

Переходная функция колебательного звена изображена на рисунке 18.

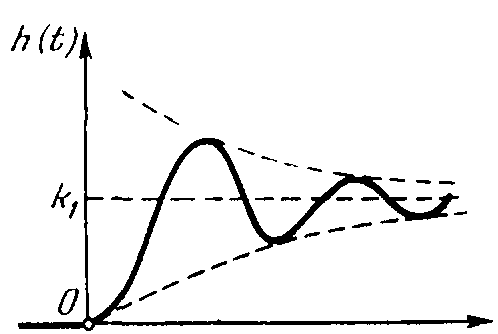
Рисунок 18 – Переходная функция колебательного звена

Она имеет вид:

h(t)=.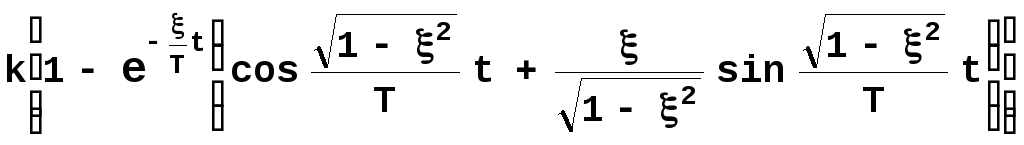

При =1 колебания вырождаются в апериодический процесс.

При =0 колебания становятся незатухающими (периодическими), и в этом случае колебательное звено носит название консервативного звена.

Примеры колебательных звеньев изображены на рисунке 19.

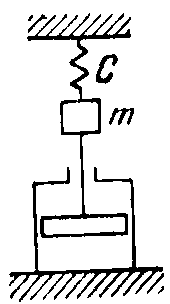
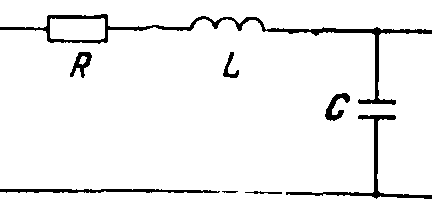
Рисунок 19 - Примеры колебательных звеньев

Идеальное интегрирующее звено

Уравнение и передаточная функция:

y(t)=k или Y(р)=X(p), W(p)=.

Амплитудно-фазовая частотная характеристика звена (рисунок 20):

W(j)=-j, A()=, ()=-90°.

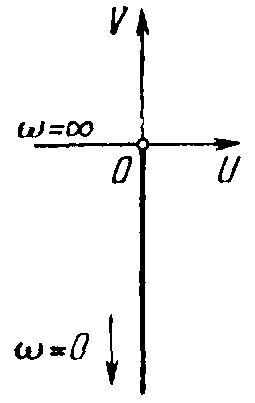
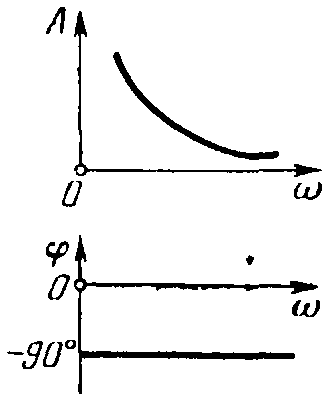
Рисунок 20 – Частотные характеристики интегрирующего звена

Логарифмическая амплитудная частотная характеристика

L()=20lgk-20lg

показана на рисунке 21 вместе с фазовой частотной характеристикой.

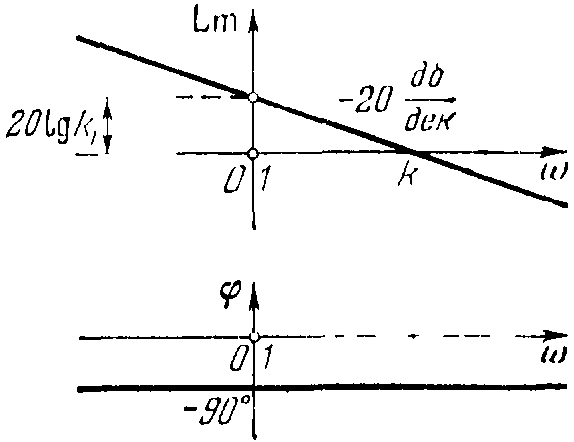
Рисунок 21 – Логарифмические частотные характеристики интегрирующего звена

Переходная функция (рисунок 22) имеет вид:

h(t)=kt, t>0.

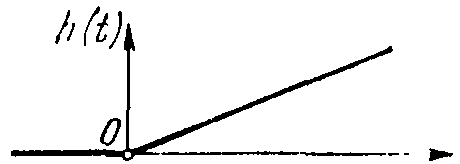
Рисунок 22 – Переходная функция интегрирующего звена

Пример идеального интегрирующего звена изображен на рисунке 23.

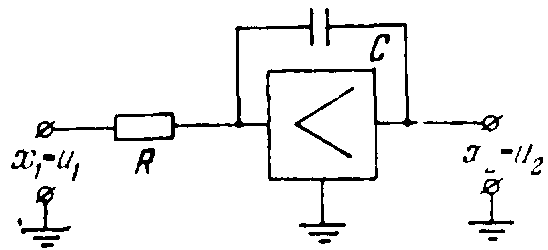
Рисунок 23 - Пример идеального интегрирующего звена

Идеальное дифференцирующее звено

Уравнение и передаточная функция звена:

y(t)=k, Y(p)=kpX(p), W(p)=kp.

Амплитудно-фазовая частотная характеристика (рисунок 24) звена:

W(j)=jk, A()=k, ()=+90°.

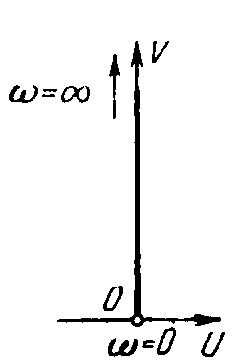
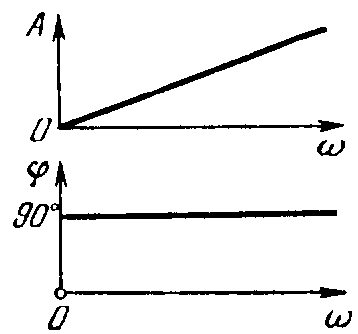
Рисунок 24 – Частотные характеристики идеального дифференцирующего звена

В реальных системах такой вид характеристик звена возможен лишь в ограниченной полосе частот.

Логарифмические частотные характеристики (рисунок 25):

L()=20lgk+20lg, ()=+90°.

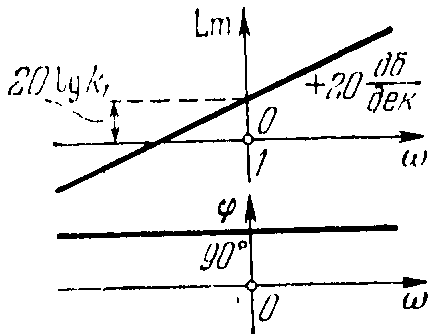
Рисунок 25 - Логарифмические частотные характеристики идеального дифференцирующего звена

Переходная функция имеет вид:

h(t)=k(t), t>0.

Примерами такого типа звена являются (рисунок 26) тахогенератор и RC-цепочка с усилителем.

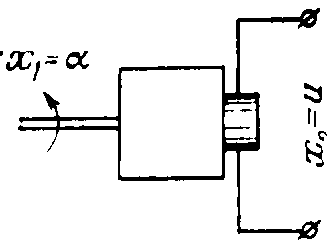
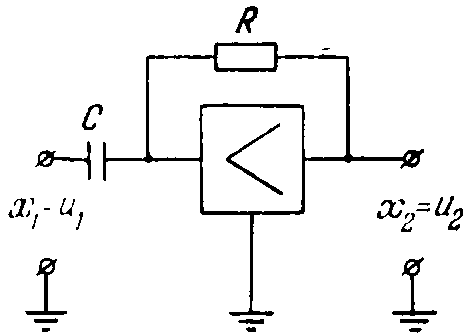
Рисунок 26 – Примеры дифференцирующих звеньев

Реальное дифференцирующее звено

Уравнение и передаточная функция звена:

(Тр+1)Y(p)=kX(p), W(p)=.

Амплитудно-фазовая частотная характеристика (рисунок 27) звена:

W(j)=, A()=, ()=90°-arctgT.

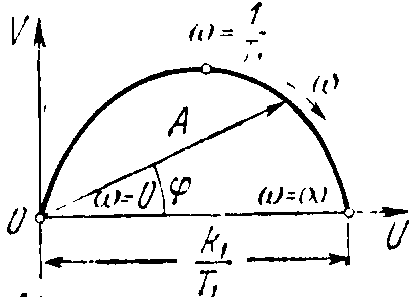
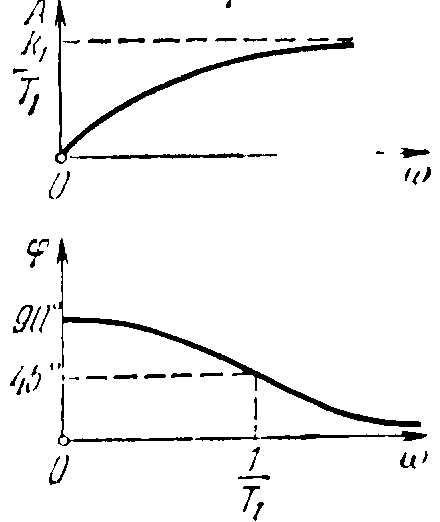
Рисунок 27 – Частотные характеристики реального дифференцирующего звена

Логарифмические частотные характеристики (рисунок 28):

L()=20lgk+20lg()-20lg, ()=90°-arctgT.

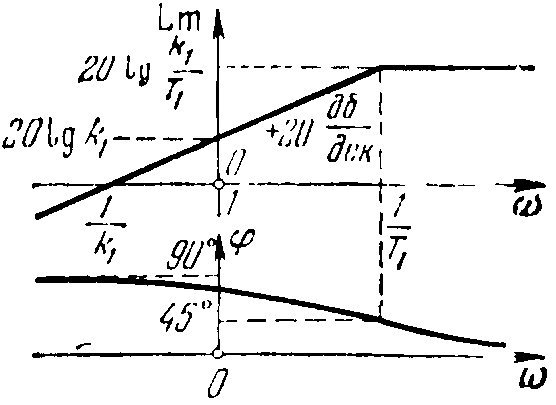
Рисунок 28 - Логарифмические частотные характеристики реального дифференцирующего звена

Переходная функция (рисунок 29) имеет вид:

h(t)=, t>0.

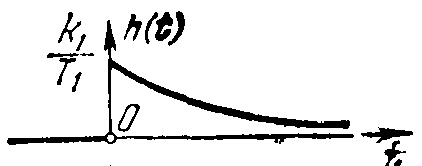
Рисунок 29 - Переходная функция реального дифференцирующего звена

Примерами такого типа звена являются обычная цепочка RC, трансформатор, механический демпфер с пружиной (рисунок 30).

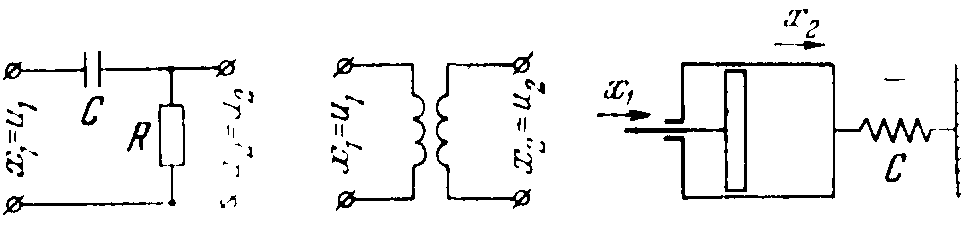
Рисунок 30 – Примеры реальных дифференцирующих звеньев