-
Показательная функция
Область
определения:
.
Область
значений:
.
Четность, нечетность: общего вида.
Периодичность: непериодическая.
Монотонность:
возрастает при
,
если
;
убывает при
,
если
.
График: рис. 7.8
-
Логарифмическая функция
Область
определения:
.
Область
значений:
.
Четность, нечетность: общего вида.
Периодичность: непериодическая.
Монотонность:
возрастает при
,
если
;
убывает при
,
если
.
График: рис. 7.9
-
Тригонометрические функции
Область
определения:
.
Область
значений:
.
Четность, нечетность: нечетная.
Периодичность:
период
.
Монотонность:
возрастает при
;
убывает при
,
.
График: рис. 7.10
Область
определения:
.
Область
значений:
.
Четность, нечетность: четная.
Периодичность:
период
.
Монотонность:
возрастает при
;
убывает при
,
.
График: рис. 7.11
Область
определения:
,
.
Область
значений:
.
Четность, нечетность: нечетная.
Периодичность:
период
.
Монотонность:
возрастает при
,
.
График: рис. 7.12
Область
определения:
,
.
Область
значений:
.
Четность, нечетность: нечетная.
Периодичность:
период
.
Монотонность:
убывает при
,
.
График: рис. 7.13
-
Обратные тригонометрические функции
Область
определения:
.
Область
значений:
.
Четность, нечетность: нечетная.
Периодичность: непериодическая.
Монотонность:
возрастает при
.
График: рис. 7.14
Область
определения:
.
Область
значений:
.
Четность, нечетность: общего вида.
Периодичность: непериодическая.
Монотонность:
убывает при
.
График: рис. 7.15
Область
определения:
.
Область
значений:
.
Четность, нечетность: нечетная.
Периодичность: непериодическая.
Монотонность:
возрастает при
.
График: рис. 7.16
Область
определения:
.
Область
значений:
.
Четность, нечетность: общего вида.
Периодичность: непериодическая.
Монотонность:
убывает при
.
График: рис. 7.17
Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).
Алгебраической называется функция, в которой производится конечное число алгебраических действий с аргументом. К ним относятся:
-
целая рациональная функция, или многочлен:
; -
дробно-рациональная функция, или отношение двух многочленов;
-
иррациональная функция (если в действиях с аргументом имеется извлечение корня).
-
Преобразование графиков
Полное исследование функции и построение графиков осуществляется с помощью производной. Но существуют приемы построения графиков функций с помощью преобразования графиков основных элементарных функций.
Пусть задан график
функции
.
-
График функции
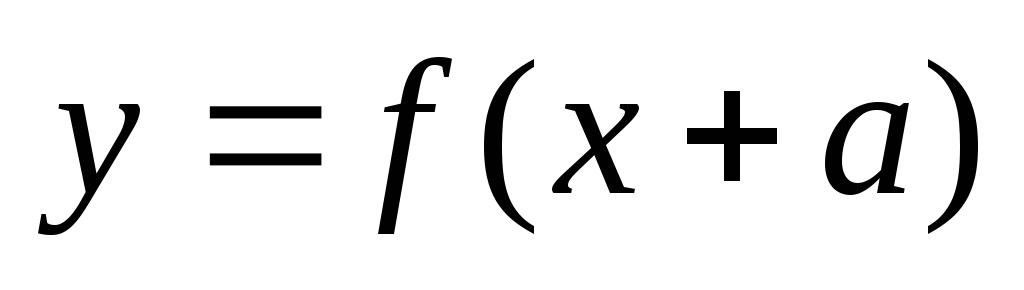получается из графика функции
в
результате сдвига вдоль оси
на
единиц влево, если
,
и вправо, если
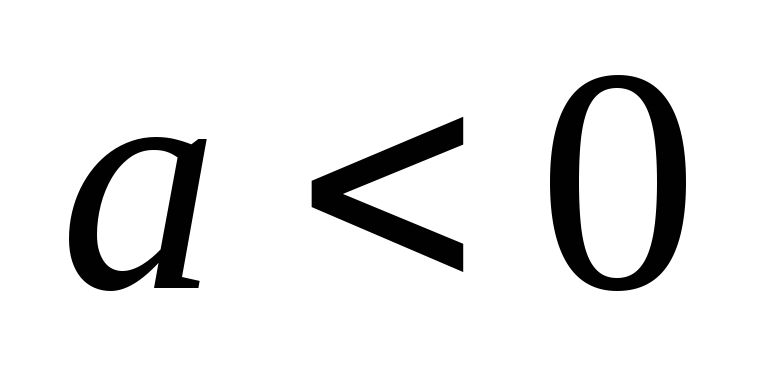(рис.
7.18). -
График функции
получается из графика функции
в
результате сдвига вдоль оси
на
единиц вверх, если
,
и вниз, если
(рис.
7.19). -
График функции
получается из графика функции
в
результате сжатия вдоль оси
в k раз, если
,
и растяжения в
раз, если
(рис.
7.20).
-
График функции
получается из графика функции
в
результате растяжения вдоль оси
в k раз, если
,
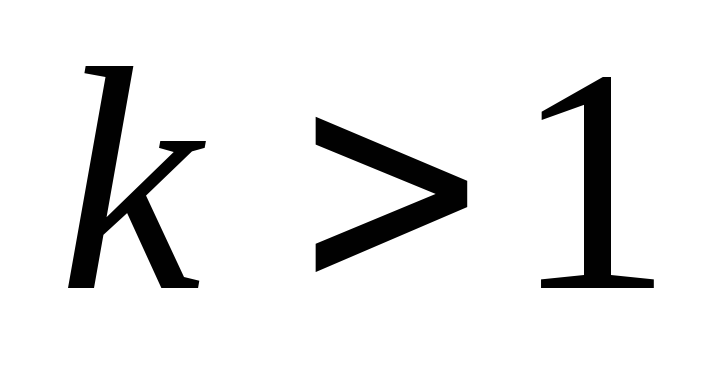и сжатия в
раз, если
(рис. 7.21). -
График функции
симметричен графику функции
относительно
оси абсцисс (рис.
7.22). -
График функции
симметричен графику функции
относительно
оси ординат (рис.
7.23). -
График функции
симметричен графику функции
относительно
оси ординат и совпадает с графиком
функции
при
(рис.
7.24). -
График функции
совпадает с графиком функции
в тех точках, которые лежат выше оси
абсцисс, и симметричен графику функции
относительно
оси абсцисс в остальных точках (рис.
7.25).
УПРАЖНЕНИЯ
Найти область определения функции
7.14.
.
7.15.
.
7.16.
.
7.17.
. 7.18.
.
7.19.
.
7.20.
.
7.21.
.
7.22.
.
7.23.
.
Определить, какие из данных функций являются четными (нечетными).
7.24.
.
7.25.
.
7.26.
.
7.27.
.
7.28.
.
7.29.
.
7.30.
.
7.31.
.
7.32.
.
Найти основной период функций
7.33.
.
7.34.
.
7.35.
.
7.36.
.
7.37.
.
Построить графики функций
7.38.
.
7.39.
.
7.40.
.
7.41.
.
7.42.
.
7.43.
.
7.44.
.
7.45.
.
7.46.
.
О Т В Е Т Ы К У П Р А Ж Н Е Н И Я М