шпоргалка / Sonic

ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ.

Ступенчатый сигнал.

f(t)=1, при t≥0

f(t)=0, при t≤0

Ступенчатый сигнал является отдельным элементом импульсного сигнала:

Если ∆t→0, то

Дельта импульс.

Дельта импульс является математической абстракцией, реально не может быть получен. Он применяется только при теоретическом анализе системы.

На практике этот импульс формирует конечные амплитуды, но амплитуда импульса не должна превышать предельно допустимой для данной системы.

Пусть на вход системы воздействует единичный ступенчатый сигнал. Реакция системы по выходу на ступенчатое единичное воздействие называется переходной функцией h(t).

x(t)=h(t), при u(t)=1(t); (1)

- по Лапласу.

(2).

Подадим на вход системы воздействие. Реакция системы на выходе в этом случае называется импульсной переходной или весовой функцией q(t).

x(t)=q(t) при u(t)= (3).

(4).

(5) - по Лапласу.

(6).

Применим к правой части выражения (6) второе свойство преобразования Лапласа:

(7).

(8) => (9).

Полученные функции q(t) и h(t) – это реакции системы на внешнее воздействие. Обе реакции описывают поведение системы во времени, поэтому называются временными характеристиками.

Для разных систем переходная функция h(t) – результат воздействия одного и того же сигнала 1(t). Таким образом, функция h(t) показывает отличие одной системы от другой. По характеру h(t) можно распознать систему, т.е. выполнить её идентификацию.

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ САУ.

Комплексное число и его представление на плоскости .

Формы представления:

1) Полярная форма

М(ρ, φ) ρ – модуль, φ – фаза

2)Показательная форма

- сдвиг фазы

3)Тригонометрическая форма

M=ρ(cosψ+sinψ)

4)Алгебраическая

M=a+jb=Re + jIm

Если на вход системы подавать синусоидальные сигналы с постоянной амплитудой и частотой, то после затухания переходных процессов на выходе так же возникает синусоидальное колебание с той же частотой, но с другой амплитудой и сдвинутой по фазе относительно входных колебаний.

Рассмотрим реакцию линейного звена на гармоническое возмущение при условии, что корни характеристического уравнения звена отрицательны, т.е переходный процесс, зависящий от общего решения однородного дифференциального уравнения, является затухающим, действительная часть : , мнимая: . Тогда гармоническое возмущение в комплексной тригонометрической плоскости: (1)

Согласно формуле Эйлера выражение (1) имеет вид:

(2)

(3)

(4)

Т.е. мы можем записать входную величину (3) и выходную (4) в комплексной показательной плоскости.

Если начальная фаза равна 0, то

(5)

(6)

Запишем дифференциальное уравнение звена в операторной форме

(7)

(8)

Подставим (5) и (6) в (7):

(9)

Отношение выходных величин системы к входным с учетом сдвига по фазе называется амплитудно-фазовой характеристикой.

Модуль амплитудно-фазовой характеристики звена или отношение амплитуды выхода и входа называется амплитудно-частотной характеристикой.

(10)

Зависимость разности фаз входных и выходных колебаний от частоты называется фазо-частотной характеристикой звена и является аргументом амплитудно-фазовой характеристики. Амплитудно-фазовая характеристика не зависит от времени, в этом её отличие от переходной функции. Если временная характеристика определяет поведение системы в переходном процессе, то АФХ выражает зависимость параметров установившихся выходных колебаний от тех же параметров входных колебаний при различных частотах. АФХ отображает только установившиеся процессы.

Запишем дифференциальное уравнение системы в общем случае:

(11)

φ и μ – выходная и входная величины звена в отношениях от состояния звена.

и - постоянные коэффициенты, определяемые конструктивными особенностями и параметрами настройки звена.

ПОРЯДОК НАХОЖДЕНИЯ АЧХ И ФЧХ:

1. Определяем передаточную функцию звена или системы

2. Производим замену операторов p на jw , т.е. получаем частотную передаточную функцию.

3. Выделяем Re и Im частотной передаточной функции.

4. Задаваясь значениями ω от 0 до +∞, строим АЧХ и ФЧХ по выражению(25,26)

(25) - АЧХ

(26) - ФЧХ

ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМЫ

Для каждого звена будем рассматривать следующие характеристики:

1. Передаточная функция

2. Дифференциальное уравнение

3. Переходная функция

4. Весовая или импульсная переходная функция

5. АФЧХ

6. Реализация звена

ИНЕРЦИООНОЕ ЗВЕНО

k – коэффициент усиления; T – постоянная времени.

- дифференциальное уравнение инерционного звена

H(p)=W(p) - переходная функция

Переходный процесс инерционного звена экспоненциален. Установившееся значение в числе равно коэффициенту усиления. Касательная пересекает линию установившегося значения в точке t=k

H(T)=0.63 k

В автоматике принято считать время переходного процесса по достижении 5% окрестности установившегося значения.

Годограф описывает окружность с наиболее низкой точкой, при этом фазовый сдвиг равен π/4 при изменении частоты от 0 до +∞. Радиус-вектор АЧХ монотонно убывает от начального k, стремясь к 0.

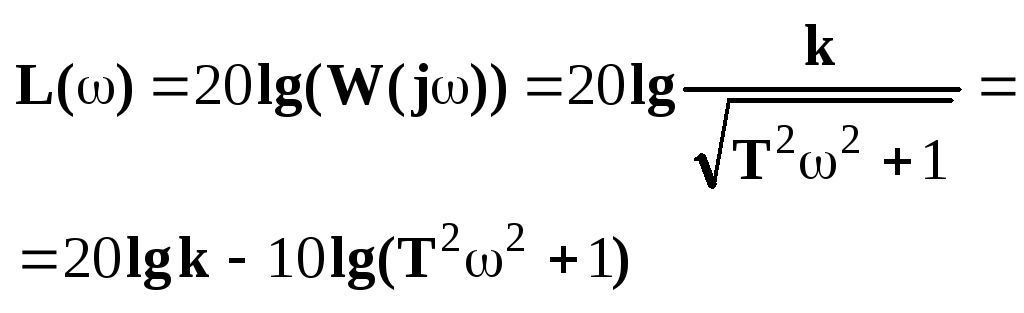
ЛАЧХ:

- +20

- +40

- +60

…….

- k в числителе, значит наклон положительный

P -20

Tp+1 - 20

- 40

Реальная трансцендентная функция является ЛАЧХ инерционного звена. Чтобы упростить использование ЛАЧХ вводят понятие асимптотических характеристик, т.е. кусочно-постоянных функций, не отличающихся от истинных. Выделяем области низких и средних частот. По отдельности рассмотрим поведение ЛАЧХ в этих областях. После этого оценим максимальную ошибку, возникающую на границе областей.

Низкие частоты:

Можно пренебречь

Средние частоты:

Наклон асимптотической кривой

Максимальная ЛАЧХ достигается в точке 1/T. Выведено, что диапазон в 3∂Б от максимальной ошибки является полосой пропускания системы.

(12)

(13)

(14)

(15)

Учитывая (12,13,14,15) перепишем (11):

(16)

Из (16) определим АФХ системы:

(17)

Перепишем выражение (16) в операторной форме:

(18)

Из (18) получим передаточную функцию:

(19)

Сравнивая (17) и (19) отметим, что для получения АФХ системы или звена достаточно в выражении передаточной функции оператор p заменить на jw.

Рассмотрим полиномы Q(jw) и P(jw):

(20)

(21)

Выделим в полиномах Re и Im :

(22)

(23)

Таким образом, полиномы представляют собой комплексные числа.

(24) - АФХ системы.

Построение выражения (24) затруднительно. Для анализа систем желательно построить отдельно ФЧХ и ФЧХ. Эти характеристики дают максимальный объем информации о системе, поэтому для их построения используются следующие выражения:

(25) - АЧХ

(26) - ФЧХ

При изменении ω от -∞ до +∞ строят графическое изображение АЧХ, ФЧХ на комплексной плоскости. Очевидно, что вещественная часть является четной функцией. Так частота входит в числитель и знаменатель только в четных степенях. Таким образом, точки АФХ, соответствующие значению ω и –ω имеют одну и туже абсциссу и равные по модулю, но разные по знакам ординаты. Следовательно, АФХ симметрична относительно действительной оси и достаточно построить её только для значений от 0 до +∞, т.к. другая ветвь характеристики является зеркальным отображением построенной части относительно действительной оси. АФХ называется годографом вектора, изображающим на комплексной плоскости передаточную функцию при изменении частоты от 0 до +∞.

Длина вектора, проведенного из начала координат в какую либо точку АФХ, соответствующей частоты, равен модулю частотной передаточной функции и показывает отношение амплитуды выходного и входного сигнала.

Угол между вектором и положительной вещественной полуоси отсчитывают против часовой стрелки, он равен аргументу частотной передаточной функции при заданной частоте и показывает сдвиг фаз выходного и входного сигнала системы или звена при этой частоте.

СТРУКТУРНЫЙ АНАЛИЗ.

Система управления состоит из некоторого набора звеньев. Т.к. характеристики отдельных звеньев изучены, то получить свойства системы можно через известные параметры звеньев. Для преобразования входных сигналов в выходные, звенья системы могут соединяться тремя способами: а)последовательно, б)параллельно, в)последовательно параллельно (с обратной связью).

а)

б)

в)

Все формулы справедливы в том случае, если на вход поступает только одно воздействие(управляющее). Реальная система автоматически подвержена воздействию возмущающих величин, которые могут поступать в систему в любом месте и влиять на выходную величину.

Прямая цепь системы состоит из элементов G1, G2, G3. На два последних элемента действует возмущающее воздействие, суммирующееся соответствующими величинами предыдущих звеньев. Возмущение F3 действует на выходную величину системы, что обозначено элементом суммировании, при этом важно, что место приложения F3 охвачено обратной связью, т.е. и на звено Z(p) поступает выходная величина системы с учетом внешнего воздействия . Таким образом, управляющая величина системы, искаженная возмущением F3, корректируется обратной связью. Возмущающие воздействия F2, F3 поступают на вход звеньев через дополнительные звенья Gf2 b Gf3, которые отражают характер зависимости системы от конкретного возмущающего воздействия . В силу линейности рассматриваемой системы в ней применим принцип наложения, который даёт возможность определить общую реакцию системы, т.е изменение выходной величины как сумму частных реакций от каждого возмущения в отдельности.

РЕАЛИЗАЦИЯ ИНТЕГРИРУЮЩЕГО ЗВЕНА

1. Интегрирующим звеном является RCC

k=1, T=RC

2)

k=-∞, Rвых=0, Rвх=∞, Свх=0. Имеет идеальную АЧХ.

3)

В электрических схемах добавляя или убирая обратные связи можно либо усилить, либо ослабить звено.

При реализации инерционного звена в электрических схемах необходимо учитывать следующие условия:

1. Ограниченность линейного диапазона операционного усилителя сказывается на качестве его работы при больших сигналах.

2. Узкая полоса пропускания операционного усилителя ухудшает работу инерционного звена.

3. При выборе операционного усилителя необходимо учитывать: а) конечность усиления б) ненулевую входную емкость в) ненулевое выходное и небесконечное входное сопротивления.

4. Неидеальная частотная характеристика

5. Нелинейная амплитудная характеристика