Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Исследование решений дифференциального уравнения первого порядка аналитическим и численным методами

Методические указания

по выполнению лабораторной работы по курсу

«Теория автоматического управления»

для студентов специальности 120100

всех форм обучения

Одобрено

редакционно-издательским советом

Балаковского института техники,

технологии и управления

Балаково 2008

1. Цель работы. Изучение решений дифференциального уравнения первого порядка при различных исходных данных. Освоение аналитического и численного метода Эйлера решения дифференциальных уравнений. Освоение работы в электронных таблицах Excel.

2. Постановка задачи. Задано дифференциальное уравнение первого порядка, описывающее работу элемента

системы управления (рис. 1)

,

где - соответственно, входной и выходной сигналы элемента,

- коэффициент передачи и постоянная времени элемента.

Необходимо:

1. Освоить аналитическое решение дифференциального уравнения.

2. Разработать программу решения данного уравнения методом Эйлера в электронных таблицах Excel.

3. Освоить необходимые исходные данные для решения дифференциального уравнения.

4. Найти решения уравнения при различных начальных условиях, коэффициентах уравнения и законах изменения входного сигнала x(t).

5. Сравнить аналитическое и численные решения.

1. Решение дифференциального уравнения аналитическим путем

Решение дифференциального уравнения заключается в нахождении зависимости изменения во времени выходной переменной при следующих исходных данных:

• дифференциальное уравнение с параметрами k,Т;

• начальное значение выходной переменной ;

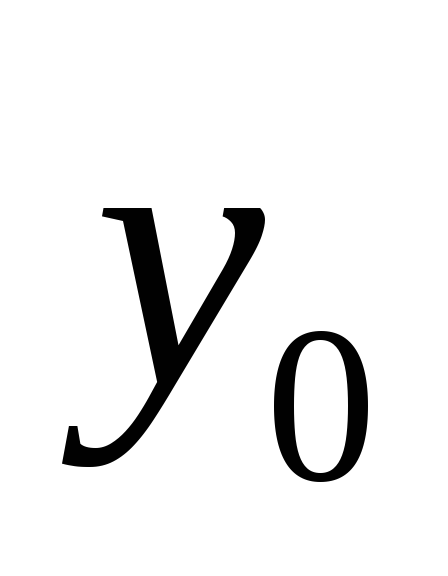• закон изменения во времени входной переменной .

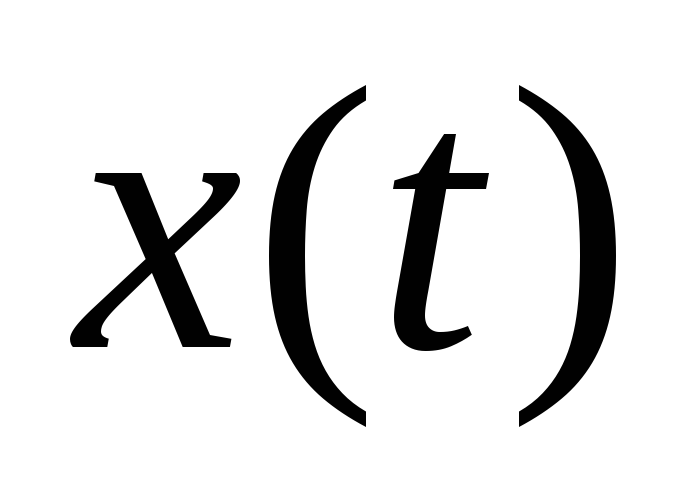Найдем решение дифференциального уравнения при постоянном значении входного сигнала .

Решение ищем в виде суммы свободной и вынужденной составляющих

1. Находим свободную составляющую решения:

- запишем характеристическое уравнение ;

- найдем корень уравнения ;

- запишем свободную составляющую решения дифференциального уравнения:

.

2. Находим вынужденное решение. Входной сигнал 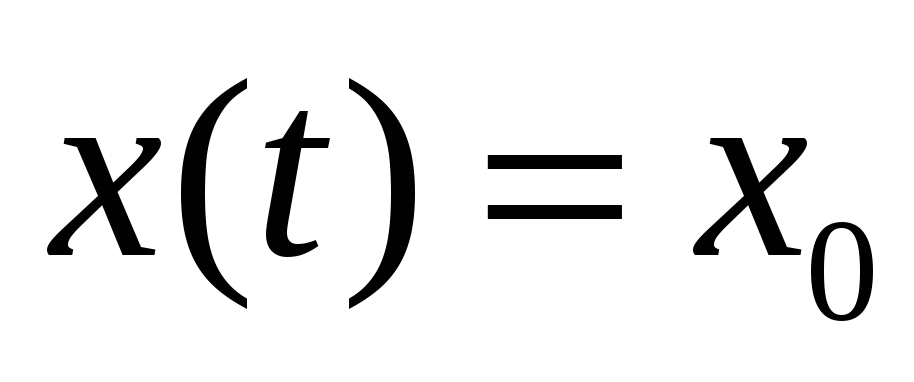относится к полиномам. Поэтому ищем решение в виде такого же полинома

.

Для нахождения значения В подставляем решение в исходное уравнение

, , тогда .

Вынужденная составляющая .

3. Общее решение

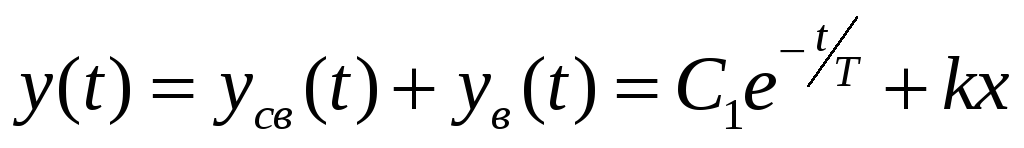
4. Используя начальные условия, найдем постоянную :

при

, отсюда

5. Решение уравнения при постоянном входном сигнале

.

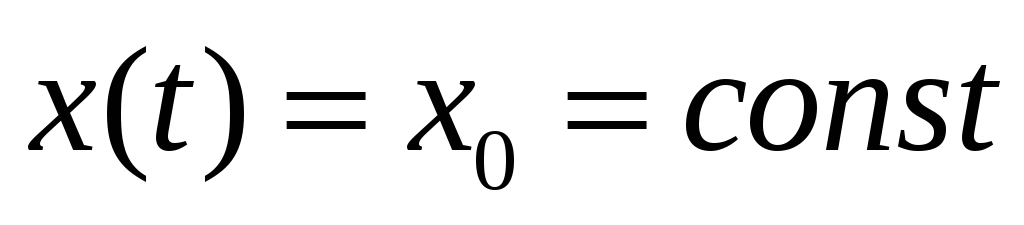
Первый элемент выражения отражает влияние начальных условий и показывает, что начальное значение уменьшается по экспоненциальному закону с постоянной времени Т.

Второй элемент выражения отражает влияние входного сигнала при нулевых начальных условиях и показывает, что при подаче на вход звена первого порядка постоянного сигнала выходной сигнал по экспоненциальному закону с постоянной времени Т выходит на значение .

Время падения первого элемента и выхода второго элемента на расчетное значение с точностью 5% (вход в 5% трубку от расчетного значения) называется временем переходного процесса и составляет .

4. Метод Эйлера. При численном решении дифференциального уравнения время берется в дискретные моменты:

.

Непрерывный входной сигнал заменяется ступенчатым дискретным сигналом

Пусть есть решение дифференциального уравнения при начальном значении . Следующее значение можно определить из треугольника .

Суть метода Эйлера заключается в замене криволинейного треугольника abc (рис. 2) на прямоугольный abd. Тогда значение выходной переменной при будет

Из прямоугольного треугольника abd .

Тогда следующее значение можно определить по его предыдущему:

.

На основании геометрического смысла производной тангенс угла наклона касательной равен значению производной функции в данной точке , которое можно определить по дифференциальному уравнению: .

Заменяя производную на отношение , запишем выражение для значения на основания значений и в предыдущей точке:

.

Аналогично запишем выражения для всех последующих значений

; … ;

В общем случае разностное рекуррентное уравнение имеет вид:

.

Таким образом, используя данное уравнение, можно последовательно точка за точкой найти решение уравнения первого порядка при заданных , параметрах уравнения и известному входному сигналу .

5. Первый этап работы. Получить решение дифференциального уравнения при единичном ступенчатом входном сигнале

и нулевых начальных условиях .

1. Включить компьютер и вызвать программу Excel.

2. Присвоить файлу название и записать на жесткий диск. В дальнейшем периодически (один раз в 10-15 мин производить перезапись файла).

3. В первой строке таблицы ввести номер лабораторной работы, фамилию и инициалы студента, номер группы.

4. Разработать таблицу для решения дифференциального уравнения (по образцу):

   1. Подготовить шапку таблицы параметров и ввести параметры дифференциального уравнения k, T в верхней части столбца 3. Значения k, Т принимаются равными количеству букв в имени и фамилии студента.

   2. Ввести шаг по времени, равный .

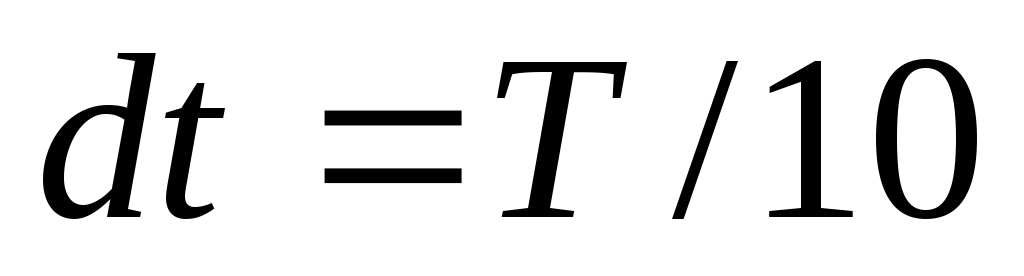   3. Ввести нулевое начальное значение .

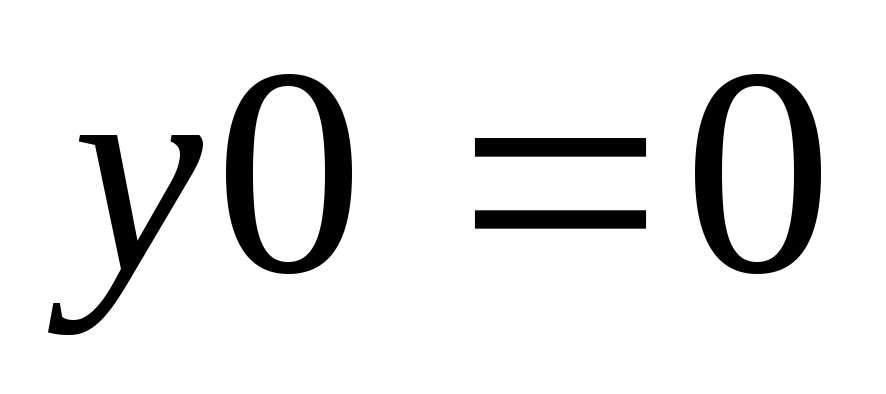   4. Ввести значение входного сигнала .

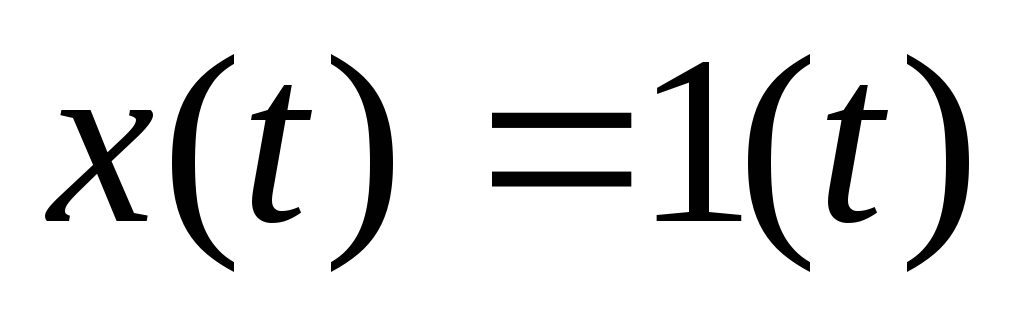   5. Подготовить шапку таблицы решения дифференциального уравнения.

   6. Путем «протаскивания» номера строки заполнить столбец № п/п.

   7. Заполнить столбец времени путем протаскивания формулы .

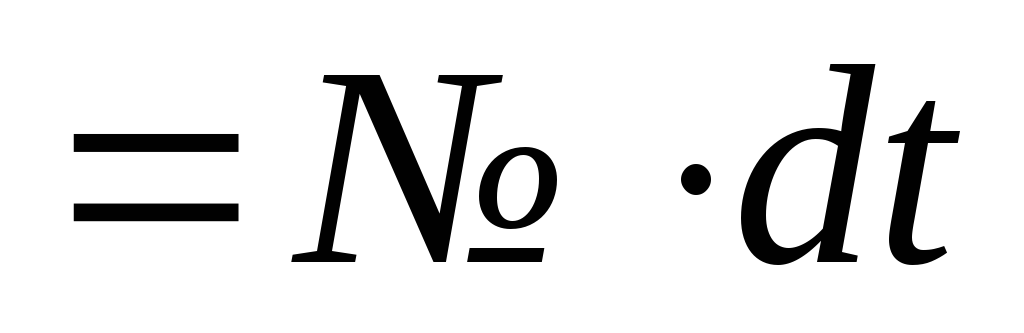   8. Ввести формулу ввода столбца входного сигнала из ячейки .

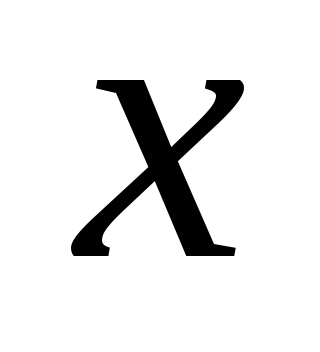   9. Записать начальное значение y в нулевой строке столбца 4 .

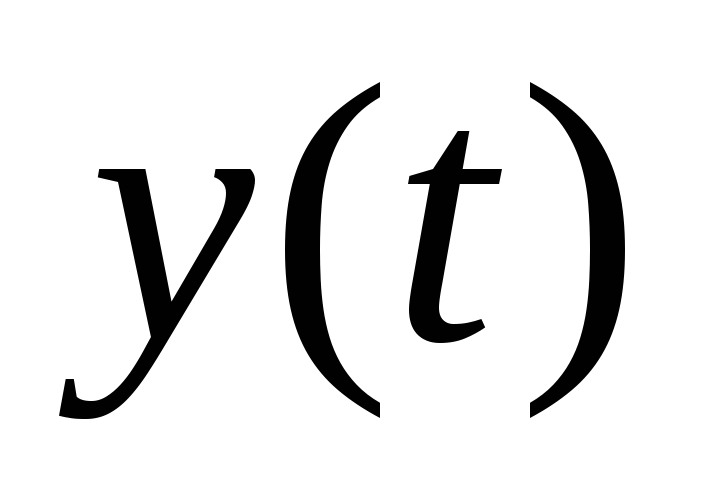
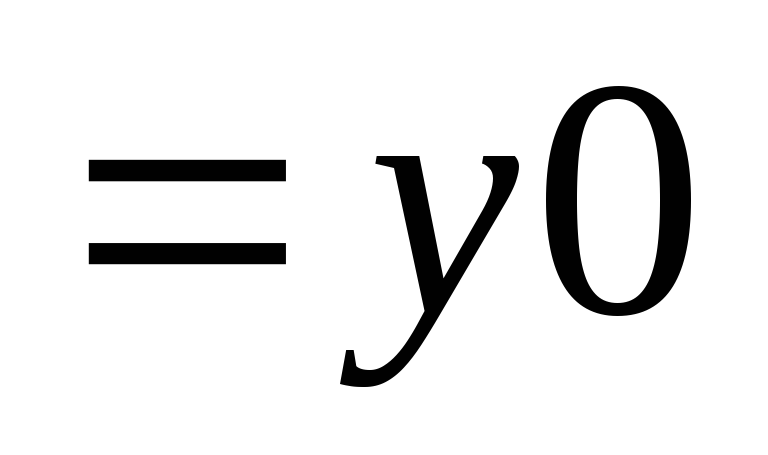   10. Ввести формулу расчета производной в столбец 5

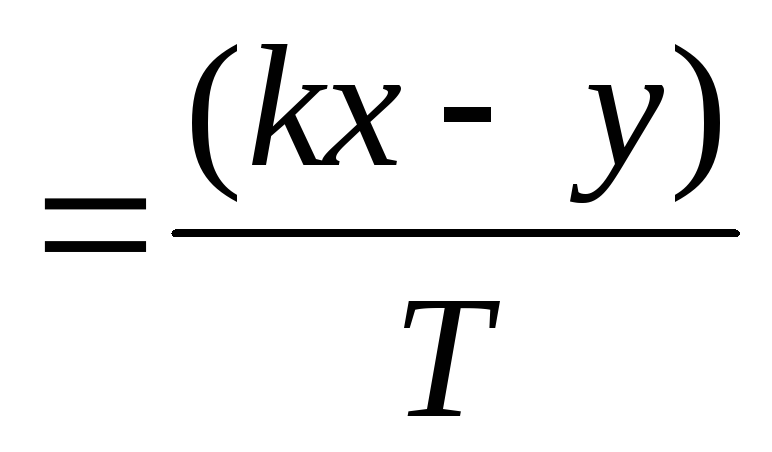
по значениям в предыдущей строке.

1. Начиная со второй строки столбца 4, ввести рекуррентное уравнение Эйлера для расчета текущего значения 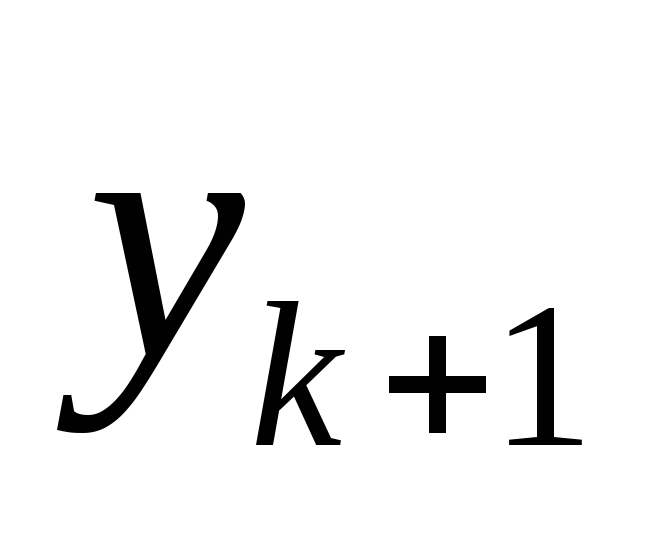по значениям элементов уравнения в предыдущей строке. .

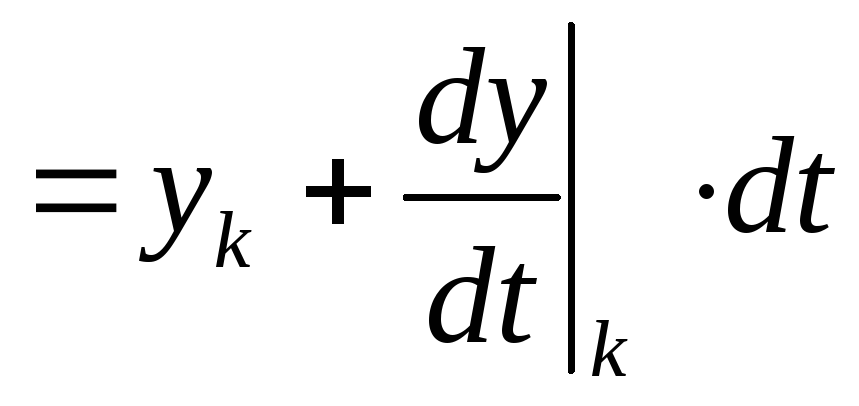1. Построить график полученного решения уравнения.

2. Используя функцию «Специальная вставка», перенести полученное решение в столбец 6.

1. Второй этап работы. Рассчитать и построить графики трех семейств решений уравнения для различных значений:

• начальных условий;

• входного сигнала;

• коэффициентов уравнения.

В верхней части столбцов 7-9 готовится таблица данных с изменяющимися начальными условиями; столбцов 10-12 - с изменяющимся коэффициентом передачи звена; столбцов 13-15 - с изменяющейся постоянной времени звена.

Для каждой комбинации исходных данных находятся решения путем переноса столбца данных в данные столбца 3, а полученных решений из столбца 4 с помощью команды «Специальная вставка» в столбцы 7-9; 10-12; 13-15.

Первое семейство кривых находится при постоянных значениях параметров и изменяющихся начальных условиях (НУ) и входном сигнале.

1-й расчет - при нулевых НУ и постоянном входном сигнале;

2-й расчет - при ненулевых НУ и нулевом входном сигнале;

3-й расчет - при ненулевых НУ и ненулевом входном сигнале.

Второе семейство кривых – исследование влияния коэффициента усиления звена при нулевых начальных условиях и постоянном входном сигнале.

Третье семейство кривых – исследование влияния постоянной времени звена при нулевых начальных условиях и постоянном входном сигнале.