7.2. Примеры решения типовых задач

Пример 1. 17,5 г CuSO₄ растворено в 420 мл воды. Рассчитайте массовую долю, моляльную и молярную концентрации и титр полученного раствора, если его плотность ρ = 1,04 г/мл.

Решение. При решении задачи необходимо использовать приведенные выше формулы для расчета различных способов выражения концентрации раствора.

Определение массовой доли ω(CuSO₄) в %

1. Найдем массу полученного раствора:

так как ρ(Н₂О) = 1 г/мл, то m(Н₂О) = ρ(Н₂О) ∙ V(Н₂О) = 1 г/мл ∙ 420 мл = 420 г,

m_р-ра = m(CuSO₄) + m(Н₂О) = 17,5 + 420 = 437,5 г.

2. Рассчитаем массовую долю CuSO₄ в полученном растворе (в %). Воспользуемся формулой (7.1.2):

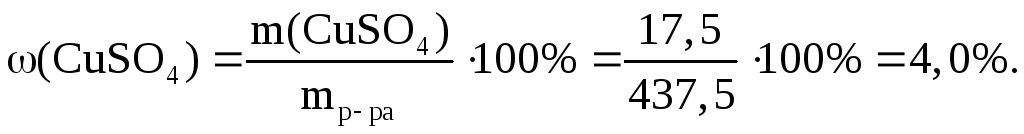
Определение моляльной концентрации раствора

Для расчета моляльной концентрации воспользуемся формулой (7.1.5).

1. Масса растворителя (воды) в килограммах равна:

m(H₂O) = 420 г = 0,42 кг.

2. Число моль CuSO₄ в растворе равно:

n(CuSO₄) = моль.

3. Моляльная концентрация раствора CuSO₄ равна:

моль/(кг H₂O).

Определение молярной концентрации раствора

Для расчета молярной концентрации воспользуемся формулой (7.1.6).

1. Найдем объем раствора CuSO₄ в литрах:

420,7 мл = 0,4207 л.

2. Так как количество вещества CuSO₄ нам уже известно, мы можем найти молярную концентрацию данного раствора:

моль/л.

Определение титра раствора

Для расчета титра воспользуемся формулой (7.1.12):

г/мл.

Пример 2. Какой объем раствора КОН с массовой долей ω(КОН) = 5% и плотностью 1,04 г/мл требуется для полного осаждения ионов железа Fe³⁺ из 50 мл раствора FeCl₃ с массовой долей ω(FeCl₃) = 10% и плотностью 1,09 г/мл?

Решение.

1. Найдем массу раствора FeCl₃:

г.

2. Определим массу FeCl₃, содержащегося в 50 мл 10%-го раствора:

г.

3. По уравнению реакции

3КОН + FeCl₃ = Fe(OH)₃↓ + 3KC1

3∙56 г 162,5 г

вычисляем массу КОН, необходимого для реакции с содержащимся в растворе FeCl₃:

162,5 г FeCl₃ взаимодействуют с 168 г КОН;

5,45 г FeCl₃ ––––"–––– m г КОН;

г.

4. Зная массу КОН, концентрацию раствора и его плотность, вычисляем массу и объем раствора КОН:

г.

мл.

Пример 3. Для нейтрализации 70 мл раствора соляной кислоты потребовалось 200 мл 0,3 Н раствора NaOH. Какова молярная концентрация эквивалента HCl?

Решение. Эту задачу следует решать, используя соотношение:

C_эк(HCl) ∙ V(HCl) = C_эк(NaOH) ∙ V(NaOH),

из которого получаем:

моль/л,

следовательно, данный раствор соляной кислоты имеет молярную концентрацию эквивалента 0,86 Н.

Примечание. Молярную концентрацию эквивалента вещества необходимо рассматривать применительно к реакциям. Так, например, при полной нейтрализации серной кислоты гидроксидом натрия:

H₂SO₄ + 2NaOH = Na₂SO₄ + 2Н₂О

число эквивалентности z*(H₂SO₄) = 2; эквивалент Э(Н₂SО₄) = 1/2 ФЕ(H₂SO₄), а молярная масса эквивалента

Следовательно, в данном случае 1 Н раствором H₂SO₄ будет раствор, в литре которого содержится 49 г H₂SO₄.

Для реакции частичной нейтрализации и неполного обмена эквивалент H₂SO₄ будет определяться реакцией:

H₂SO₄ + NaOH = NaHSO₄ + Н₂О,

z*(H₂SO₄) = 1; Э(Н₂SO₄) = ФЕ(H₂SO₄), а

Поэтому в данном случае 1 Н раствором H₂SO₄ будет раствор, в литре которого содержится 98 г H₂SO₄.

Пример 4. Рассчитайте молярную концентрацию эквивалента следующих растворов: раствор АlСl₃ с молярной концентрацией 0,2 моль/л; раствор Н₃РО₄ с молярной концентрацией 0,6 моль/л; раствор Сr₂(SО₄)₃ с молярной концентрацией 0,7 моль/л, принимая максимальное значение числа эквивалентности.

Решение. Воспользуемся соотношением: С_эк(В) = z*(B) ∙ C(B).

Чтобы перейти от молярной концентрации вещества к молярной концентрации эквивалента, нужно молярную концентрацию C(В) умножить на число эквивалентности z*(B).

При обратном переходе молярную концентрацию эквивалента необходимо разделить на число эквивалентности z*(B).

Для электролитов, состоящих из однозарядных катионов и анионов (NaCl, КОН, HI и др.), молярная концентрация вещества равна молярной концентрации эквивалента вещества, т.к. у них z*(B) = 1. Для сложных электролитов (АlСl₃, Н₃РО₄, Сr₂(SО₄)₃ и др.) молярная концентрация эквивалента С_эк(В) больше, чем молярная концентрация вещества С(В), т.к. у них z*(B) > 1.

Для солей АlСl₃ и Сr₂(SО₄)₃, приведенных в условии задачи, число эквивалентности определяется по числу положительных или отрицательных зарядов в молекуле, для Н₃РО₄ – по основности кислоты. Отсюда следует, что z*(АlСl₃) = 3; z*(Сr₂(SО₄)₃) = = 3∙2 = 6; z*(Н₃РО₄) = 3. Следовательно, их молярная концентрация эквивалента будет равна:

С_эк(АlСl₃) = 0,2 ∙ 3 = 0,6 моль/л;

С_эк(Н₃РО₄) = 0,6 ∙ 3 = 1,8 моль/л;

С_эк(Сr₂(SО₄)₃) = 0,7 ∙ 3 ∙ 2 = 4,2 моль/л.

Пример 5. Приготовить 70 мл раствора с массовой долей ω(H₂SO₄) = 63% (ρ = = 1,535 г/мл) путем смешения растворов с массовой долей ω₁(H₂SO₄) = 82% (ρ₁ = = 1,755 г/мл) и с массовой долей ω₂(H₂SO₄) = 34% (ρ₂ = 1,255 г/мл).

Решение. Задачу удобней решать по правилу смешения (правилу креста), согласно которому массы смешиваемых растворов обратно пропорциональны разностям концентраций смеси и отдельных ее компонентов.

1. Записываем друг под другом массовые доли исходных растворов, а правее между ними массовую долю раствора, который необходимо приготовить. Затем из большей массовой доли вычитаем заданную и записываем результат справа внизу; из заданной массовой доли вычитаем меньшую и записываем результат справа вверху:

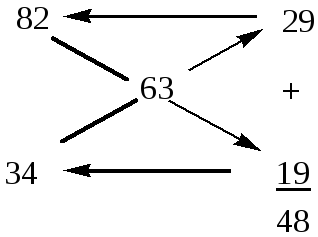
Числа 29 и 19 показывают, в каком массовом отношении надо взять растворы с ω₁(H₂SO₄) = 82% и ω₂(Н₂SО₄) = 34%, соответственно. То есть для приготовления 48 г раствора серной кислоты с массовой долей ω(Н₂SО₄) = 63% необходимо смешать 29 г раствора с ω₁(Н₂SО₄) = 82% и 19 г раствора с ω₂(Н₂SО₄) = 34%.

2. Определим массу раствора серной кислоты с массовой долей ω(H₂SO₄) = 63%:

m_{63% р-ра} = ρ_{63% р-ра} ∙ V_{63% р-ра} = 1,535 ∙ 70 = 107,45 г.

3. Определим массу и объем раствора с массовой долей ω₁(H₂SO₄) = 82%, необходимого для приготовления искомого раствора.

Для приготовления 48 г 63%-го р-ра необходимо взять 29 г 82%-го р-ра;

для приготовления 107,45 г 63%-го р-ра –––––"–––– m г 82%-го р-ра;

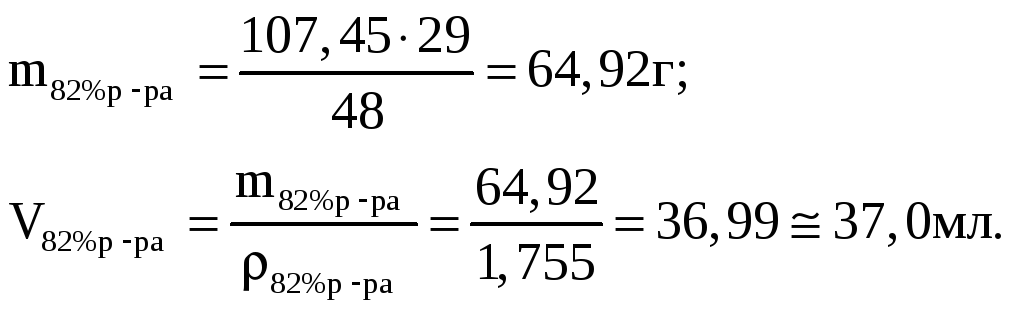
4. Определим массу и объем раствора с массовой долей ω₂(H₂SO₄) = 34%, необходимого для приготовления искомого раствора:

для приготовления 48 г 63%-го р-ра необходимо взять 19 г 34%-го р-ра;

для приготовления 107,45 г 63%-го р-ра –––––"–––– m г 34%-го р-ра;

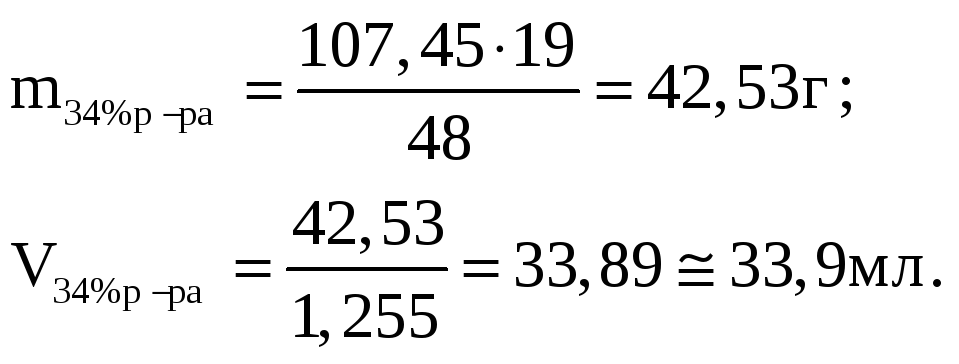
Таким образом, для приготовления 70 мл раствора с ω(H₂SO₄) = 63% нужно смешать 37,0 мл 82%-го и 33,9 мл 34%-го растворов.

Пример 6. Сколько граммов кристаллогидрата Cu(СН₃СОО)₂∙Н₂О и раствора с массовой долей ω₁(Cu(СН₃СОО)₂) = 3% нужно взять для приготовления 580 г раствора ацетата меди с массовой долей ω(Cu(СН₃СОО)₂) = 25%.

Решение. Сложность этого примера состоит в том, что кристаллогидрат содержит воду, которая добавляется при приготовлении раствора к воде, взятой в качестве растворителя. Имеется несколько способов решения. Приведем один из них.

1. Кристаллогидрат Cu(СН₃СОО)₂∙Н₂О можно рассматривать как твердый водный раствор. Определим массовую долю ω₂(Cu(СН₃СОО)₂) в кристаллогидрате:

Cu(CH₃COO)₂∙H₂O Cu(CH₃COO)₂

М = 200 г/моль М = 182 г/моль

в 200 г Cu(CH₃COO)₂∙H₂O содержится 182 г Cu(СH₃СОО)₂;

в 100 г Cu(CH₃COO)₂∙H₂O –––––"–––– х г Cu(СH₃СОО)₂;

г.

Следовательно, кристаллогидрат Cu(СН₃СОО)₂∙Н₂О представляет собой раствор с массовой долей ω₂(Cu(СН₃СОО)₂) = 91%.

2. Теперь сформулируем исходное условие следующим образом: необходимо приготовить 580 г раствора ацетата меди с массовой долей ω(Cu(СН₃СОО)₂) = 25% из растворов с массовой долей ω₂(Cu(СН₃СОО)₂) = 91% и массовой долей ω₁(Cu(СН₃СОО)₂) = 3%. Найдем их массы, используя правило смешения.

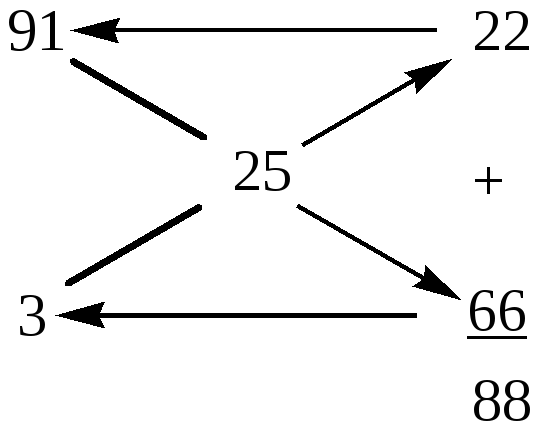
Из схемы видно, что для приготовления 88 г (22 + 66) раствора ацетата меди с массовой долей ω(Cu(СН₃СОО)₂) = 25% нужно в 66 г раствора с ω₁(Cu(СН₃СОО)₂) = 3% растворить 22 г кристаллогидрата меди. Для приготовления 580 г 25%-го раствора массы смешиваемых компонентов определяются из пропорции:

для приготовления 88 г 25%-го р-ра Cu(СН₃СОО)₂ нужно взять 66 г 3%-го р-ра;

для приготовления 580 г 25%-го р-ра Сu(СН₃СОО)₂ –––– " –––– у₁ г 3%-го р-ра;

г р-ра Cu(CH₃COO)₂ c ω₁(Cu(СH₃COO)₂) = 3%.

Аналогично найдем массу кристаллогидрата:

для приготовления 88 г 25% р-ра Cu(СН₃СОО)₂ нужно взять 22 г Cu(СН₃СОО)₂∙Н₂О;

для приготовления 580 г 25% р-ра Сu(СН₃СОО)₂ –––– " –––– у₂ г Сu(СН₃СОО)₂∙Н₂О;

г.

Таким образом, для приготовления 580 г 25%-го раствора Cu(СН₃СОО)₂ необходимо взять 145 г кристаллогидрата Cu(СН₃СОО)₂∙Н₂О и 435 г 3%-го раствора Cu(СН₃СОО)₂.

Пример 7. Определите коэффициент растворимости K (масса растворенного вещества m(В), приходящегося на 100 г растворителя, в граммах) и массовую долю растворенного вещества ω(В) (в %), если в 84,68 г насыщенного раствора содержится 14,56 г растворенного вещества.

Решение.

1. Определяем ω(В) (в %). Для этого воспользуемся формулой (7.1.2):

2. Определяем коэффициент растворимости К.

По условию масса раствора – 84,68 г, а масса растворенного вещества – 14,56 г.

Следовательно, масса растворителя равна: m(A) = 84,68 – 14,56 = 70,12 г.

На 70,12 г растворителя приходится 14,56 г растворенного вещества;

на 100 г растворителя –––– " –––– К г растворенного вещества;

г, т.е. К = 20,8 г/100 г растворителя.

Пример 8. Масса раствора, насыщенного при 343 K, равна 401,11 г. Масса воды в этом растворе на 21,11 г больше массы соли. Сколько граммов соли выделится из этого раствора, если его охладить до 293 K? Какова массовая доля соли в растворе до и после охлаждения, если в 100 г воды при 293 K растворяется 65,5 г соли?

Решение. Массу соли принимаем за m₁(В). Тогда масса воды равна:

m(Н₂О) = m₁(В) + 21,11, а их сумма m₁(В) + (m₁(В) + 21,11) = 401,11 г представляет собой массу исходного раствора. Решаем полученное уравнение относительно m₁(В):

2·m₁(В) = 401,11 – 21,11 = 380 г; m₁(В) = 190 г, следовательно, в 401,11 г насыщенного при 343 K раствора содержится 190 г соли и 211,11 г воды. При охлаждении раствора до 293 K масса воды не изменится.

По условию в 100 г воды растворяется 65,5 г соли,

в 211,11 г воды –––– " –––– х г соли,

соли.

Тогда при охлаждении из раствора выделится: 190,00 – 138,28 = 51,72 г соли. Массовую долю соли в растворе при 343 K можно найти по формуле (7.1.2):

при 343 К.

Масса раствора при понижении температуры до 293 K уменьшится на 51,72 г и будет равна: m_{2 р-ра} = 401,11 – 51,72 = 349,39 г.

Чтобы найти массовую долю соли в растворе при 293 K, снова воспользуемся формулой (7.1.2):

при 293 К.

Пример 9. При выпаривании 1 кг раствора с массовой долей NaOH 16% удалено 100 г воды. Какова массовая доля (в %) NaOH в растворе после выпаривания?

Решение. В 1 кг раствора с массовой долей ω₁(NaOH) = 16% содержится 160 г гидроксида натрия. После выпаривания 100 г воды из раствора его масса составит 900 г (m_{2 р-ра} = 1000 – 100 = 900 г), а масса NaOH останется прежней, т.е. 160 г. Найдем концентрацию раствора после выпаривания воды:

Пример 10. При температуре 293 K и давлении P = 760 мм ртутного столба в 100 г воды растворяется 71 л аммиака. Определите моляльную концентрацию и массовую долю аммиака (в %) в растворе.

Решение.

1. Поскольку объем аммиака измерен при Т = 293 K, необходимо привести его к нормальным условиям, используя соотношение :

2. Найдем число моль аммиака, занимающего объем 66,15 л. В соответствии с законом Авогадро:

1 моль NH₃ занимает объем 22,4 л (н.у.),

n моль NH₃ –––– " –––– 66,15 л,

3. Зная число моль аммиака, мы можем найти его массу: m(NH₃) = n(NH₃) ∙ M(NH₃) = = 2,95 моль ∙ 17 г/моль = 50,2 г. Масса полученного по условию раствора аммиака составит m_р-ра = m(Н₂О) + m(NH₃) = 100 + 50,2 = 150,2 г, масса растворителя (воды) равна m(Н₂О) = 0,1 кг. Моляльную концентрацию и массовую долю раствора аммиака можно рассчитать с помощью формул (7.1.5) и (7.1.2), соответственно:

моль/(кг Н₂О);

Пример 11. Рассчитайте, какие объемы концентрированной серной кислоты с массовой долей ω(H₂SO₄) = 96% и воды необходимо смешать, чтобы получить 0,5 л 20%-ной серной кислоты, если плотности растворов H₂SO₄ равны: = 1,84 г/см³, = = 1,14 г/см³.

Решение.

1. Рассчитаем массу 20%-го раствора H₂SO₄:

г.

2. Найдем массу безводной H₂SO₄ в этом растворе:

г.

3. Рассчитаем массу 96%-го раствора H₂SO₄, в котором содержится 114 г безводной серной кислоты:

г.

4. Найдем объем, занимаемый концентрированным раствором H₂SO₄ с массовой долей 96%:

см³.

5. Рассчитаем массу воды, необходимой для разбавления 96%-го раствора H₂SO₄ до 20%-го раствора:

г.

6. Так как плотность воды 1 г/см³, то объем воды численно равен ее массе, т.е.

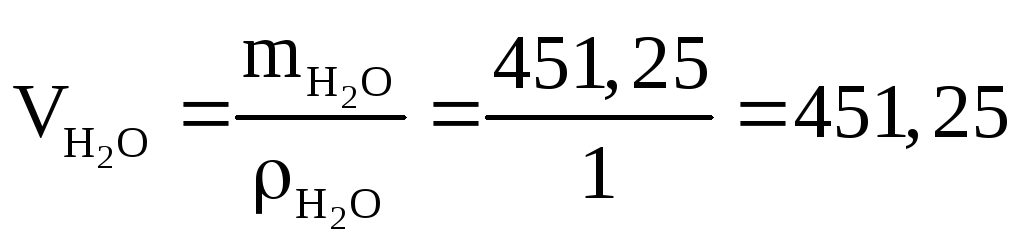см³.

Таким образом, для приготовления 0,5 л 20%-го раствора H₂SO₄ необходимо смешать 64,54 см³ 96%-го раствора H₂SO₄ и 451,25 см³ воды.

Примечание. Объем воды нельзя рассчитывать по разности объемов разбавленного и концентрированного растворов H₂SO₄. Так, 500 – 64,54 = 435,46 см³, однако это число не равно объему воды (451,25 см³), необходимому для разбавления концентрированного раствора H₂SO₄. Это несоответствие вызвано сжатием раствора при разбавлении концентрированной серной кислоты. Поэтому объем воды, необходимый для разбавления, определяют по разности масс разбавленного и концентрированного растворов, как это сделано в приведенном выше примере.