
- •Задание и исходные данные.
- •I. Анализ исходной системы
- •6. Оценка устойчивости сау
- •6.2 Оценка устойчивости сау по критерию устойчивости Михайлова.
- •6.3 Оценка устойчивости сау по критерию устойчивости Найквиста.
- •8. Определение показателей качества переходных процессов
- •II. Синтез корректирующего элемента
- •9. Расчет корректирующего элемента
- •11. Построение упрощенной структурной схемы сау с корректирующим элементом
- •11. Расчет передаточных функций сау
- •12. Расчет установившихся ошибок по задающему и возмущающему воздействиям
- •13. Оценка устойчивости сау
- •15. Определение показателей качества переходных процессов.
- •16. Заключение
11. Построение упрощенной структурной схемы сау с корректирующим элементом
Обозначим звено с передаточной функцией W234=Wэ отдельным звеном, стоящем перед корректирующим элементом в структурной схеме.

Рис.20 Упрощенная структурная схема САУ без корректирующего элемента.
В упрошенную структурную схему САУ (Рис.3) добавим корректирующий элемент.

Рис.21 Структурная схема САУ с корректирующим элементом.
Передаточная функция последовательно соединенных WeиWкорбудет равна.
![]()
![]()
В результате получим упрощенную структурную схему САУ (см. рис.22)

Рис.22 Упрощенная структурная схема САУ.
11. Расчет передаточных функций сау
11.1 Определение передаточной функции разомкнутой системы Wр(s).
![]()
11.2 Определение передаточной функции замкнутой системы Wz(s).
![]()
11.3 Определение передаточных функций ошибок.
10.3.1 Определение передаточной функции ошибки по задающему воздействию Wg∆.

Рис.23 Структурная схема САУ ошибки по задающему воздействию.
![]()
10.3.2 Определение передаточной функции ошибки по возмущающему воздействию Wz∆.

Рис.24 Структурная схема САУ ошибки по возмущающему воздействию.
![]()
12. Расчет установившихся ошибок по задающему и возмущающему воздействиям
11.1 Ошибка по задающему воздействию.
Рассчитаем ошибку по положению. Для этого воспользуемся:
![]()
Для расчета ошибки по положению принимаем:
![]()
![]()
Для расчета ошибки по скорости принимаем:
![]()
![]()
Так как ошибка системы по скорости не равна нулю, то система является астатической.
11.2 Ошибка по возмущающему воздействию.
Рассчитаем ошибку по положению. Для этого воспользуемся:
![]()
Для расчета ошибки по положению принимаем:
![]()
![]()
![]()
Так как ошибка системы по скорости не равна нулю, то система является астатической.
13. Оценка устойчивости сау
13.1 Оценка устойчивости САУ по критерию устойчивости Гурвица.
Система будет устойчива, если все определители Гурвица больше нуля, т. е. ∆1>0, ∆2>0, … , ∆n>0. Если ∆n=0, то система находится на границе устойчивости.
12.1.1 Для замкнутой системы.
Характеристический полином замкнутой
системы
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


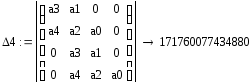
![]()
![]()
т. к. Δ1>0, Δ2>0, Δ3>0, Δ4>0, то система устойчива.
По условию устойчивости определим
предельное значение коэффициента
передачи Kгр при котором система будет
на границе устойчивости. Для этого
примем
![]() ,
при 3=0.
В результате чего получим:
,
при 3=0.
В результате чего получим:
![]()
![]()
Система находится на границе устойчивости при Kгр< 4,42.
13.2 Оценка устойчивости САУ по критерию устойчивости Михайлова.
В отличие от алгебраического критерия Гурвица, этот критерий является частотным. Он основан на построении годографа характеристического вектора A(iω).
Характеристический вектор A(iω) получается из характеристического уравнения путем заменыsнаiω.
Критерий устойчивости Михайлова формулируется следующим образом: система устойчива, если годограф характеристического вектора, начинаясь на положительной части действительной оси, обходит последовательно в положительном направлении nквадрантов, гдеn- порядок характеристического уравнения системы.
Если годограф проходит через начало координат, то система находится на границе устойчивости.
13.2.1 Для замкнутой системы.
![]()
Характеристический полином замкнутой системы:
![]()
![]()
![]()
![]()
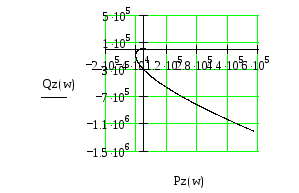
Рис.25 Годограф Михайлова для замкнутой системы.
Вывод: Система в замкнутом состоянии является устойчивой, т.к. годограф характеристического вектора начинается на положительной части действительной оси, и обходит последовательно в положительном направлении 4 квадранта. Порядок характеристического уравнения системы равен четырём.
13.2.2 Для разомкнутой системы.
![]()
![]()
![]()
![]()

![]()
Рис.26 Годограф Михайлова для разомкнутой системы.
Система является не устойчивой, т.к. годограф характеристического вектора проходит через начало координат.
13.3 Оценка устойчивости САУ по критерию устойчивости Найквиста.
Так же, как и критерий Михайлова, критерий Найквиста является частотным. Он основан на построении годографа передаточной функции H(i) разомкнутой системы.
Критерий устойчивости Найквиста формулируется следующим образом: замкнутая система устойчива, если годограф передаточной функции H(i) разомкнутой системы не охватывает на комплексной плоскости точку с координатами (-1,i0).
Если годограф проходит через точку (-1, i0), то система находится на границе устойчивости.
13.3.1 Для разомкнутой системы.
![]()
![]()
![]()
![]()
![]()

Рис.27 Годограф Найквиста для разомкнутой системы.
Система является неустойчивой, т.к. годограф Найквиста охватывает на комплексной плоскости точку с координатами (-1, i0).
13.3.2 Для замкнутой системы.
![]()
![]()
![]()
![]()
![]()
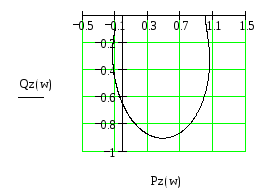
Рис.28 Годограф Найквиста для замкнутой системы.
Система является устойчивой, т.к. годограф Найквиста не охватывает на комплексной плоскости точку с координатами (-1, i0).
14. Построение АЧХ, ЛАЧХ, ФЧХ, ЛФЧХ для замкнутой и разомкнутой САУ
14.1 Построение АЧХ, ЛАЧХ, ФЧХ, ЛФЧХ для замкнутой САУ.
![]()
![]()

![]()
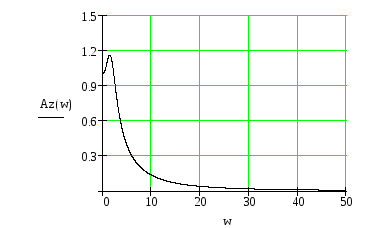
Рис.29 АЧХ замкнутой САУ.
![]()
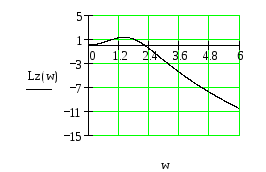

Рис.30 ЛАЧХ замкнутой САУ.
![]()
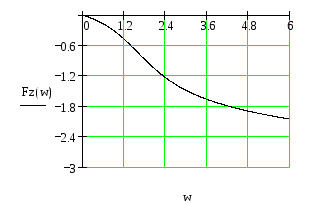

Рис.31 ФЧХ замкнутой САУ.
![]()


Рис.32 ЛФЧХ замкнутой САУ.
14.2 Построение АЧХ, ЛАЧХ, ФЧХ, ЛФЧХ для разомкнутой САУ
![]()
![]()

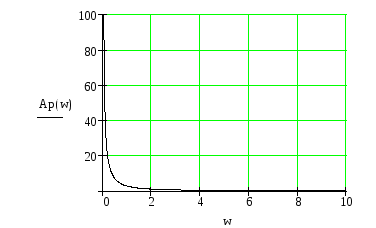
Рис.33 АЧХ разомкнутой САУ.
![]()


Рис.34 ЛАЧХ разомкнутой САУ.
![]()

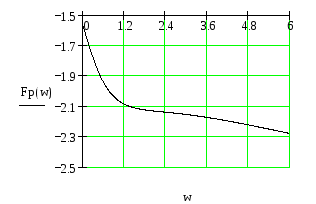
Рис.35 ФЧХ разомкнутой САУ.
![]()
![]()
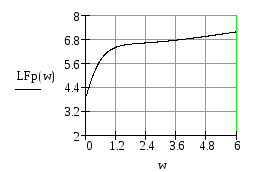
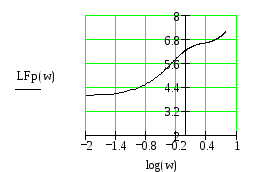
Рис.36 ЛФЧХ разомкнутой САУ.
