Étude de courbes

En géométrie, parmi les courbes remarquables il y en a une qui s’appelle « sorsière d’Agnési ». C’est la courbe étudiée par Pierre de Fermat en 1630 puis par Guido Grandi en 1703 et par Maria Gaetana Agnesi en 1748. Autre nom : versiera (diablesse en italien). Explication de ces diableries : d’après Loria, versiera est issu du latin versoria (signifiant "corde servant à virer de bord", du verbe vertere, "tourner") ; ce nom a été donné par Grandi d’après l’expression latine : sinus versus. Pour comprendre comment le sens primitif de tourner s’est transformé en sorcellerie, il faut peut-être regarder le mot adversaire, dont le correspondant italien est avversario. Toujours est-il que maintenant les anglophones appellent cette courbe : witch (sorcière) of Agnesi.

Il existe encore une courbe semblable par sa construction à celle dont il s’agit : c’est la courbe étudiée par L'Hospital et Huygens en 1692 puis par Newton en 1701. Du latin anguis  "serpent, hydre, dragon", nom donné par Newton. Autres noms : anguinea, cubique serpentine.

Ces courbes représentent les lieux géométriques définis de la façon suivante².

On se donne un cercle C et une droite D. Soit O un point du cercle C et P un point de la droite D. Soit K (KO) le point d’intersection de la droite (OP) et du cercle C. Le point M est l’intersection de la perpendiculaire à D passant par P et de la parallèle à D passant par K.

On se propose d’étudier le lieu des points M lorsque M décrit D.

On voit bien que la forme et les propriétés des courbes définies de la manière décrite ci-dessus dépendent des positions relatives d’éléments géométriques participant à sa construction (figures 2.1 et 2.2). on obtient des courbes tout à fait différentes. Donc, le but de ce TP est d’étudier dans des cas particuliers ces lieux géométriques.

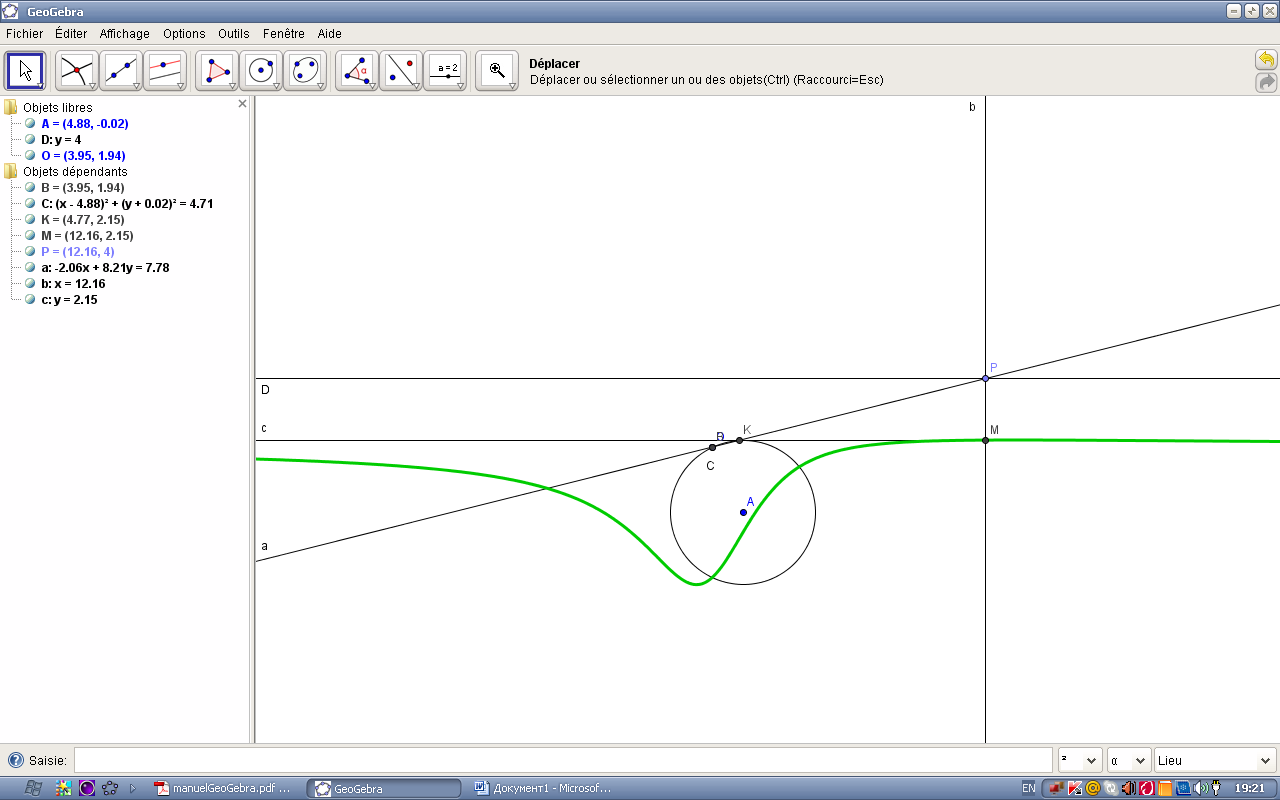
Figure 2.1. – Construction de la courbe

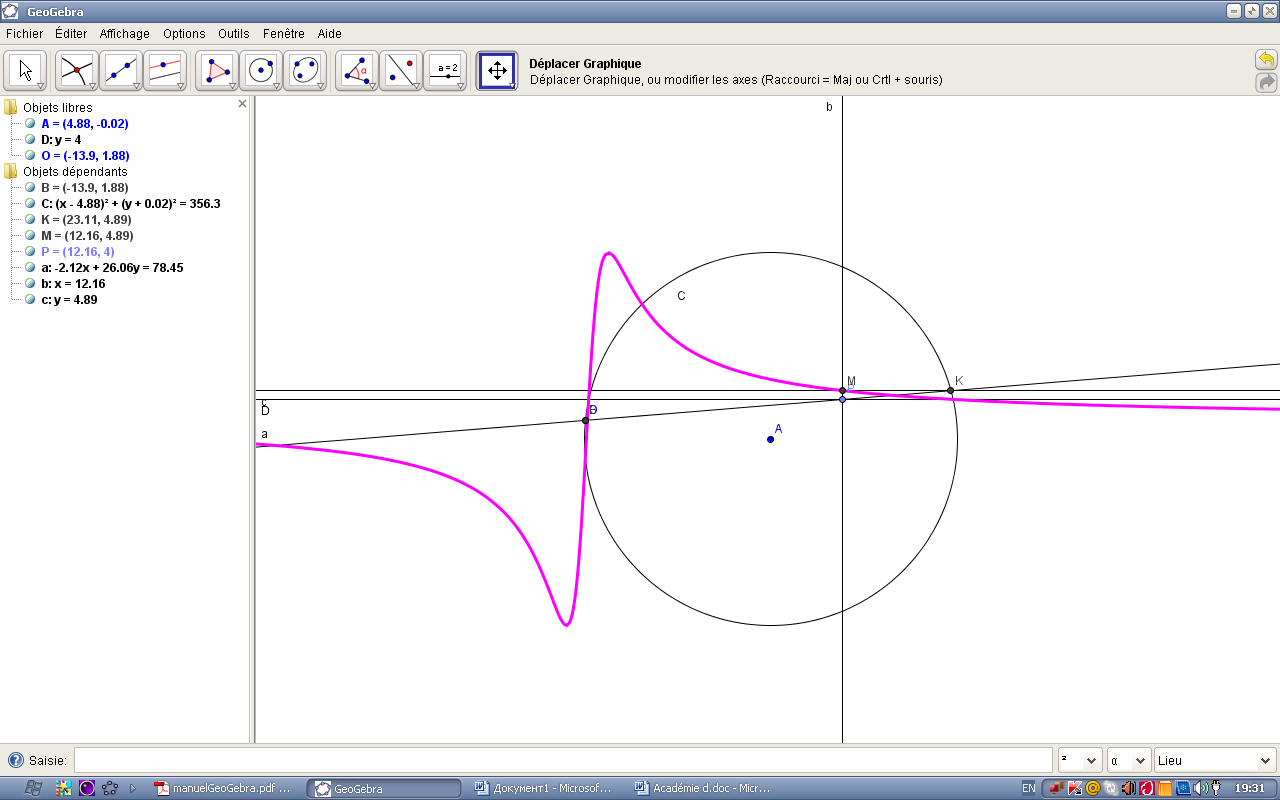
Figure 2.2. – Modification de la courbe 2.1.

Pour faire des conjectures concernant les propriétés des courbes et puis les démontrer ou rejeter analytiquement il faut construire ces courbes dans un repère pour lier deux formes : géométrique et algébrique.

Construisons ce lieu géométrique à l’aide du logiciel GéoGébra.

Tout d’abord, pour étudier les cas les plus simples, plaçons le centre du cercle sur une des axes: en premier lieu, sur l’axe des abscisses, et puis sur l’axe des ordonnées.

1. Le centre du cercle se trouve sur l’axe des ordonnées

1. On crée les points O(0,0) et A(0,2) (tapez O=(0,0), puis A=(0,2) dans la barre de saisie) et le cercle C de centre A passant par O (choisissez la boîte à outils « Cercle »).

2. On se donne un réel d=4 (il faut taper d=4 dans la barre de saisie) et la droite D d’équation y=d (tapez cette équation dans la barre de saisie).

3. On place un point P sur la droite D.

4. On construit le point K comme intersection de la droite (OP) et du cercle C (l’outil « Intersection entre deux objets » de la boîte « Point »).

5. Créez le point M comme le point d’intersection de la perpendiculaire à D passant par P (outil « Droite perpendiculaire ») et de la parallèle à D passant par K (outil « Droite parallèle »).

6. Observez la trace du point M lorsque P décrit la droite D (cliquez droit sur l’outil « Déplacer » et trînez le point P le long de la droite D) (fig. 2.3).

7. Rafraîchissez l’écran (un clic droit sur la courbe et un clic gauche sur « Effacer » dans le menu contecstuel) et créez le lieu du point M lorsque P décrit la droite D (saisissez « Lieu [M,P] » dans la barre de saisie). La trace s’obtient automatiquement (fig. 2.4).

8. Enrégistrez votre travail (menu « Fichier », commande « Sauvegarder sous... ») et imprimez votre figure.

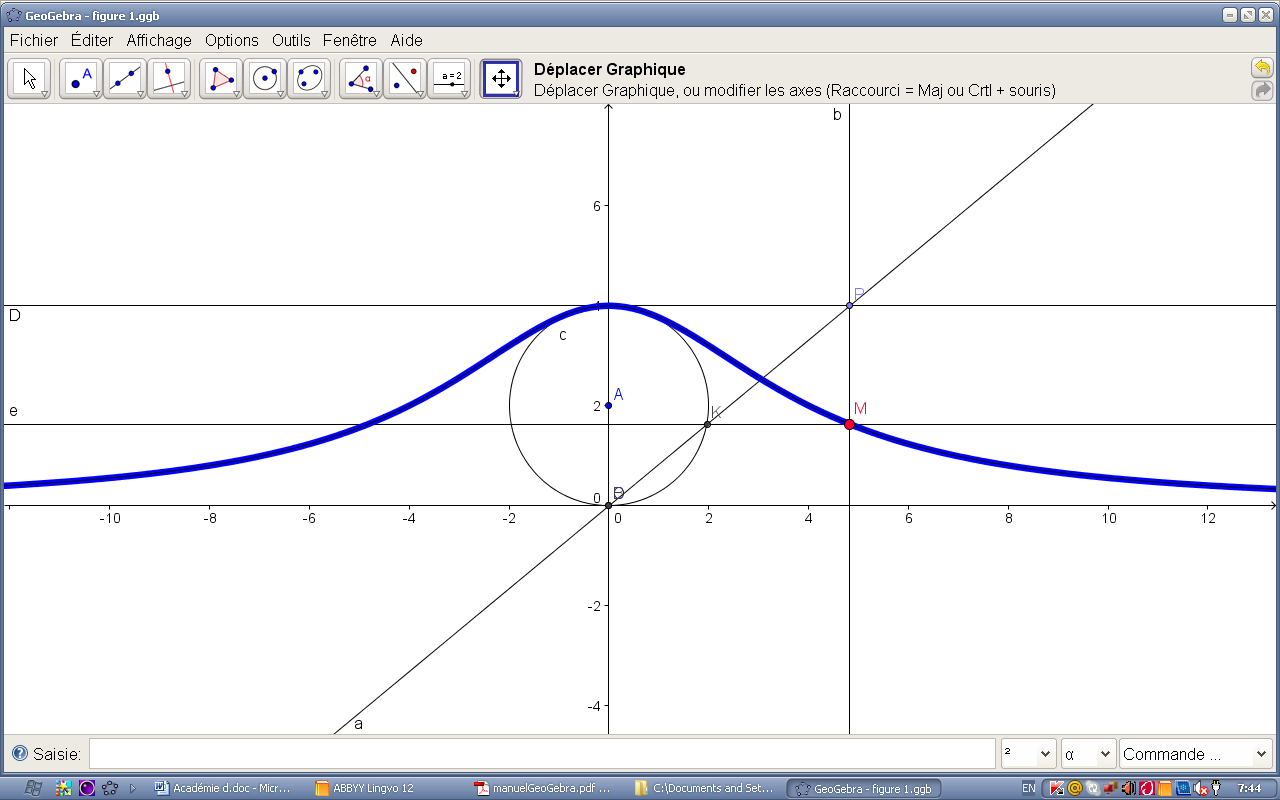
Figure 2.3. – La trace du point M

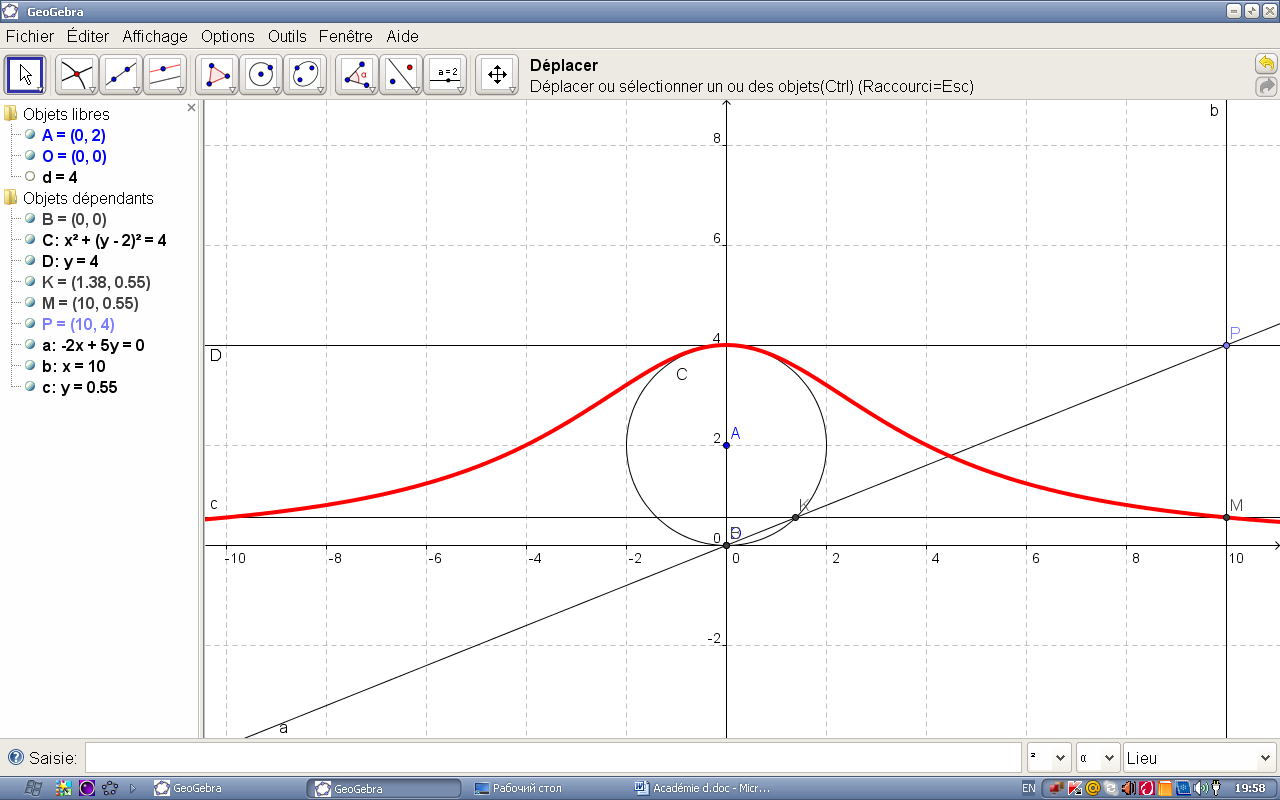
Figure 2.4. – Le lieu du point M (trace automatique)

Protocole de construction

Faites apparaître le protocole de construction (commande « Ouverture du protocole » dans le menu « Affichage ») (fig. 2.5).

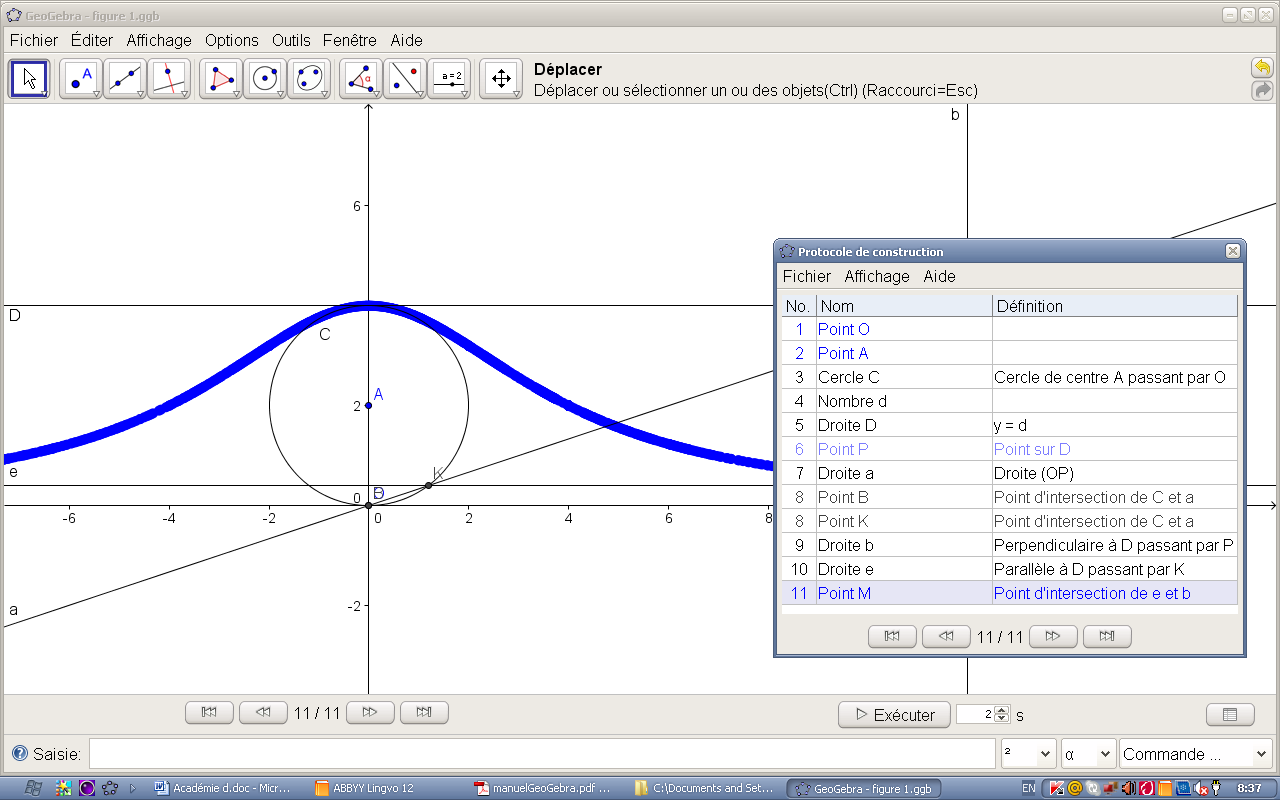
Figure 2.5. – Le protocole de construction de la courbe

Expérimentation

Dans notre cas de construction on a choisi la valeur du paramètre b égale à 4. Maintenant changeons de cette valeur et observons un changement des propriétés de la courbe.

Pour faire passer le paramètre d’une valeur à une autre, faies un clic droit sur l’objet « d=4 » dans la fenêtre « Algèbre » et dans le menu contextuel choisissez « Afficher l’objet ». Après l’avoir affiché vous verrez un curseur dans le coin gauche tout en haut de l’écran. Appuyez sur l’icon de l’outil « Déplacer » et faites glisser le curseur. Observez les changements de la courbe. Faites le protocole de changements.

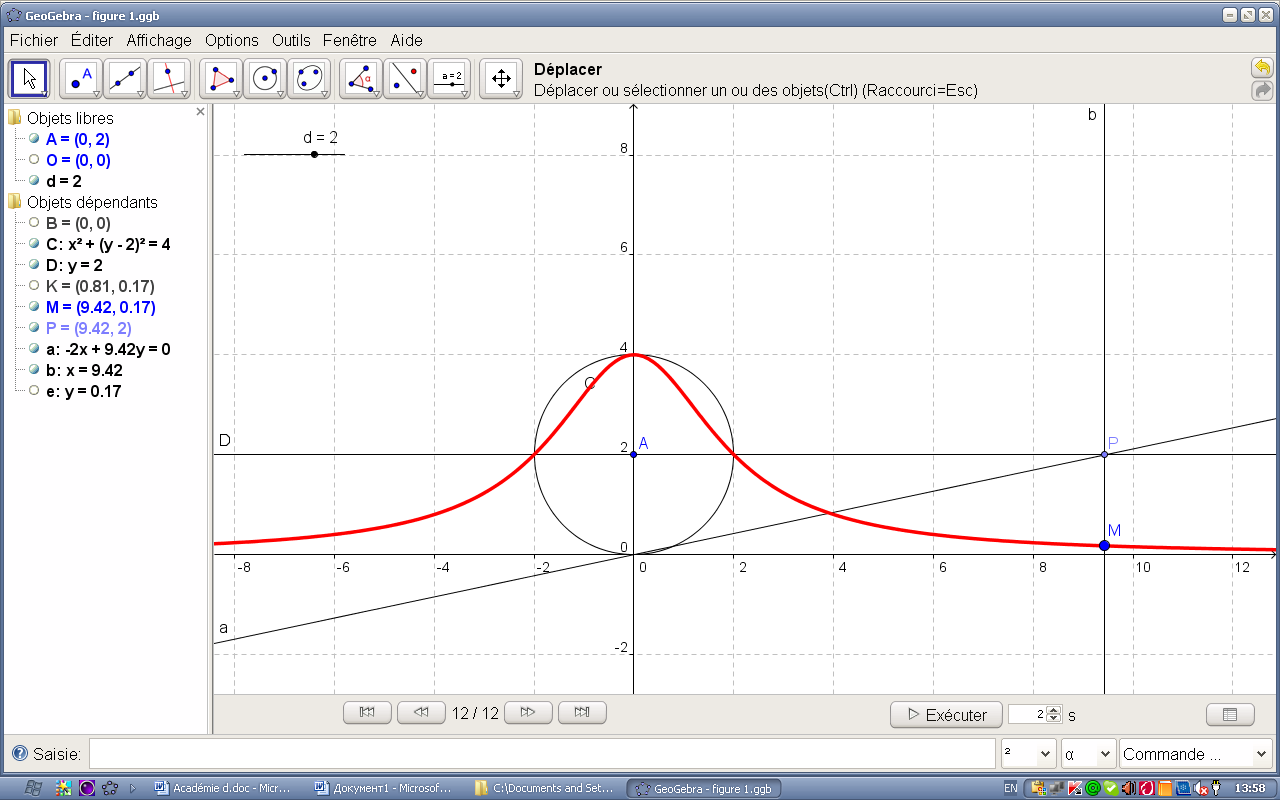
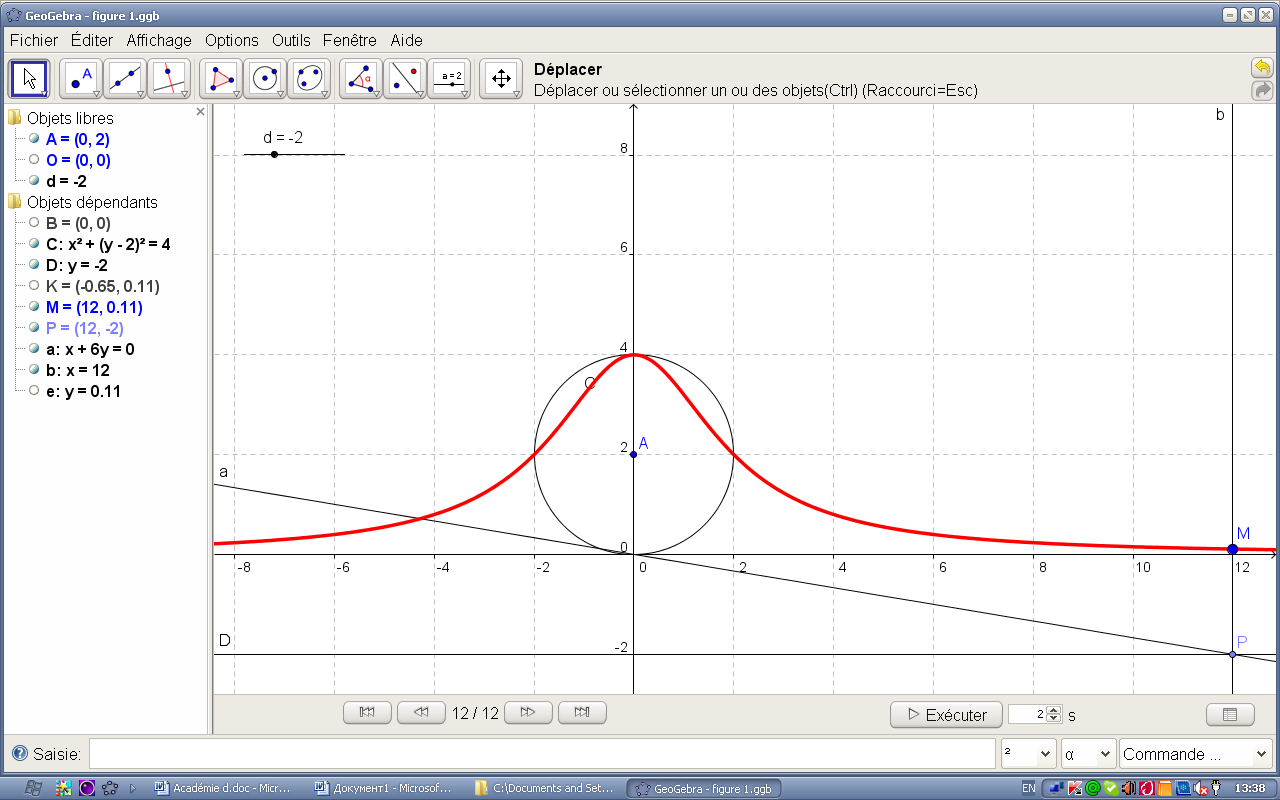
d=2	d=-2
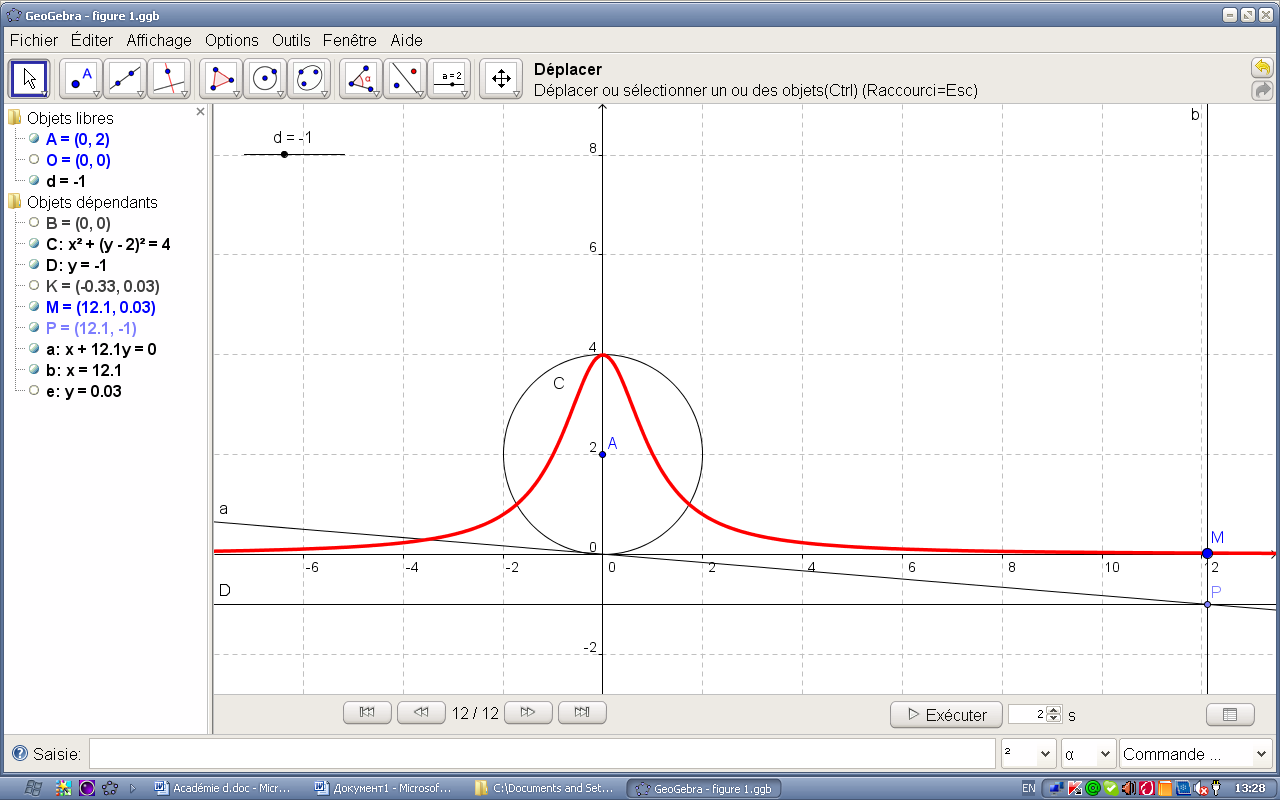
d=1	d=-1
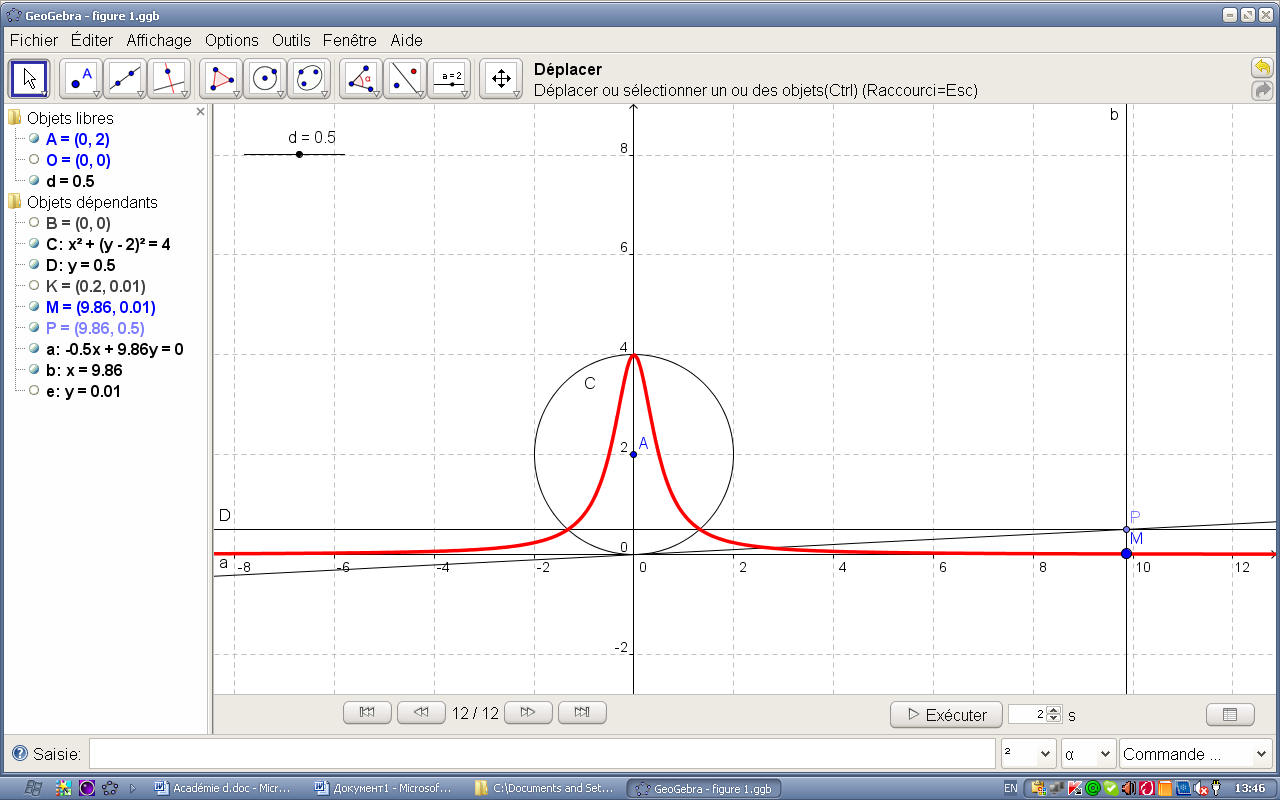
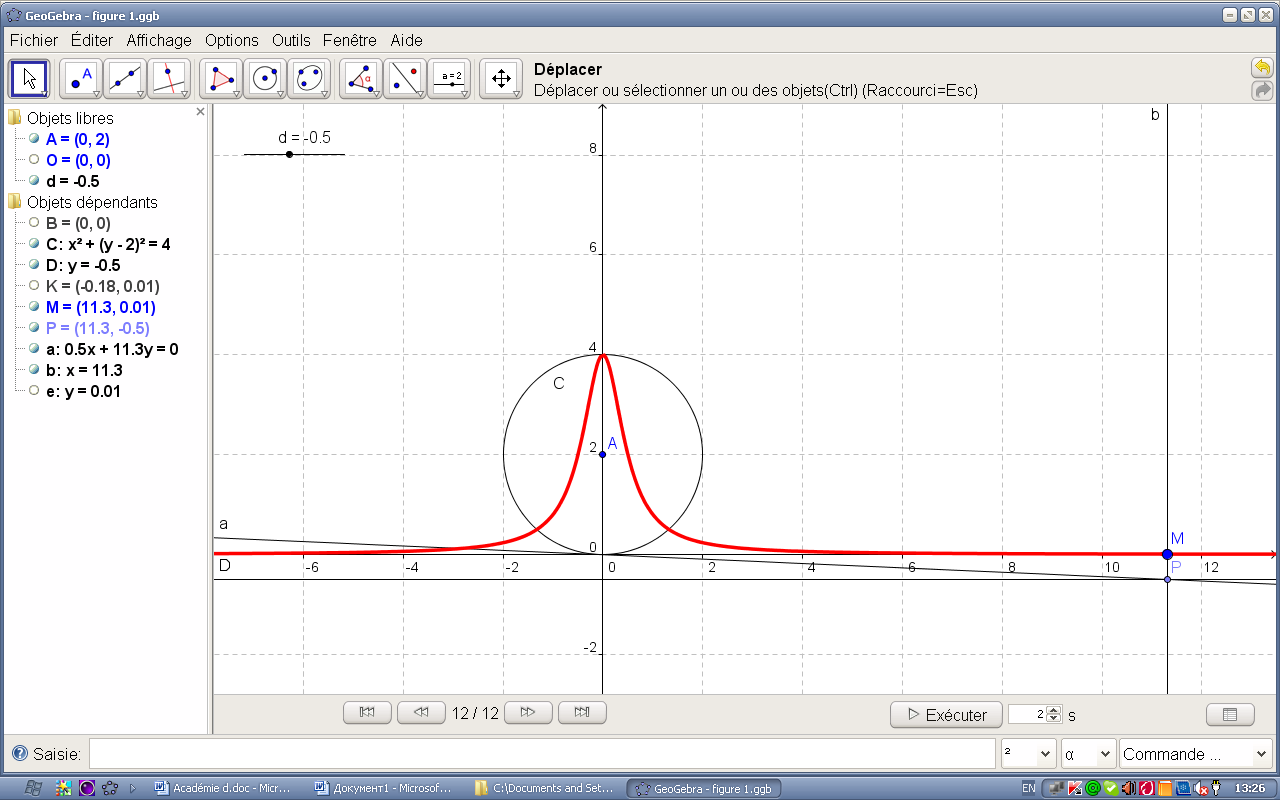
d=0,5	d=-0,5
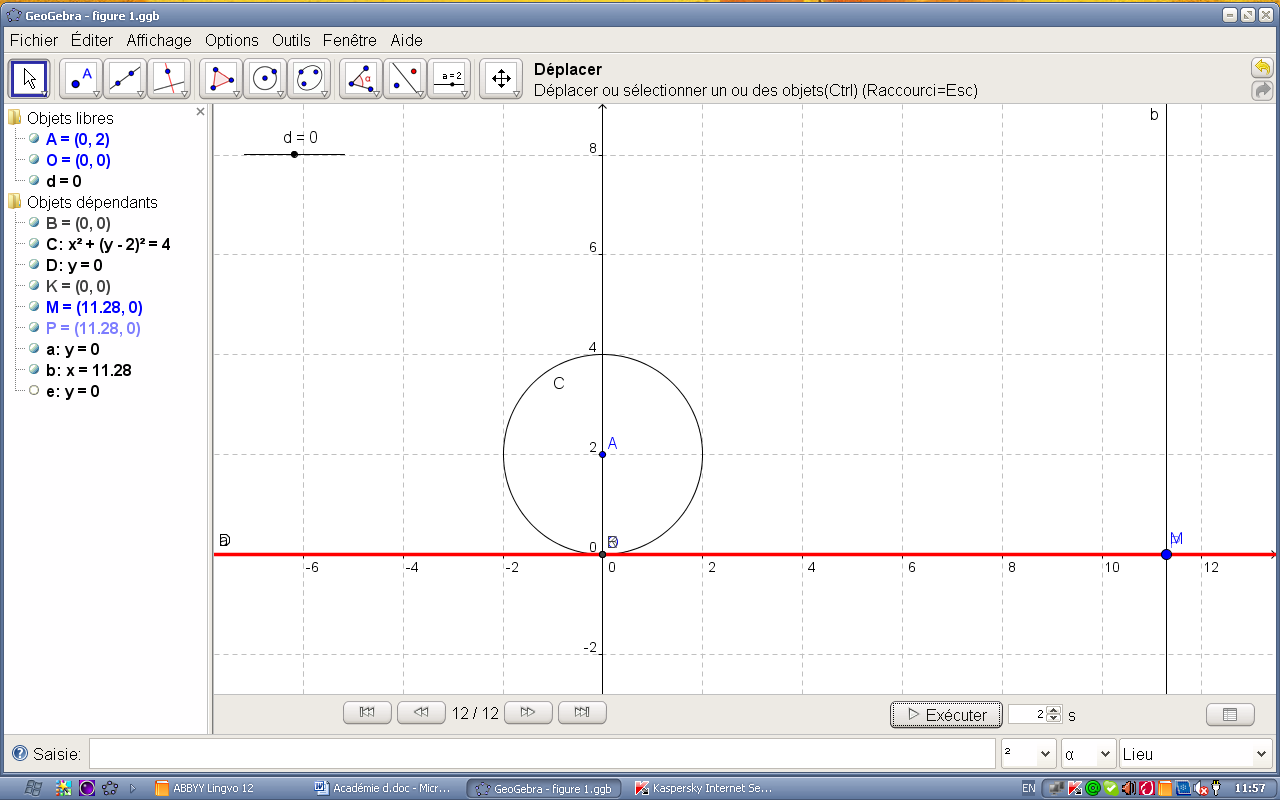
d=0

Figure 2.6. – Table de changements

Conjectures

1) Le point M décrit la courbe représentatived’une fonction f. Quelles conjectures povez-vous émettre sur cette fonction : son domaine de définition, son signe, sa parité, ses branches infinies, ses variations, son extremum ?

2) Pouvez-vous expliquer géométriquement certaines de ces conjectures (son domaine de définition, son signe, sa parité,ses branches infinies, son extremum) – on contentera d’explications succinctes.

Étude théorique

1. Lorsque le point P appartient à l’axe des ordonnées, quelle est la position du point M ?

2. D est la droite d’équation d=4 et P est un point de D d’abscisse .

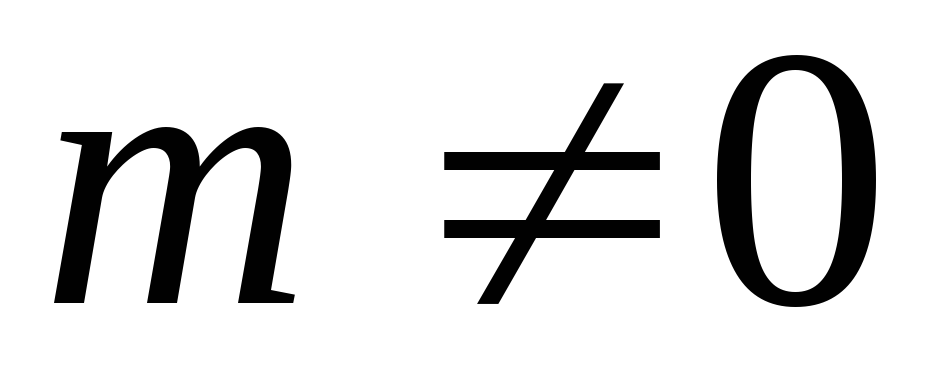   1. Donnez l’équation réduite de la droite (OP).

   2. Donnez l’équation du cercle de centre A(0,2) passant par O.

   3. Calculez les coordonnées du point K et en déduire que les coordonnées du point M sont .

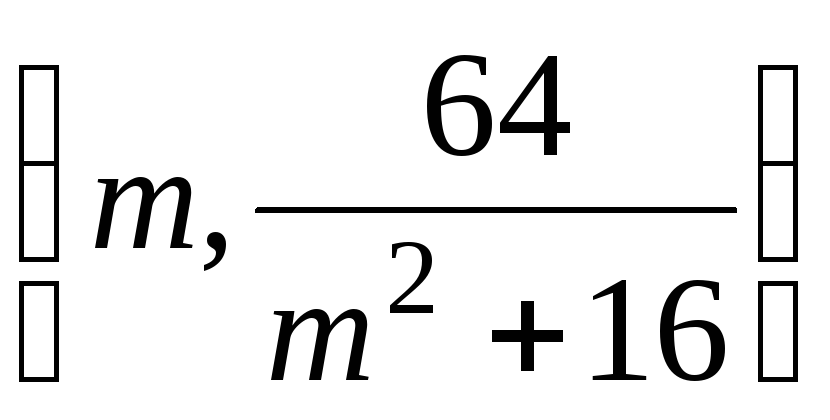   4. En déduire que le point M appartient à la courbe L d’équation .

   5. Démontrez les conjectures émises auparavant.