
- •Линейная сау «разомкнутый принцип управления»
- •1.Построить математическую модель сау.
- •2. Составить дифференциальное уравнение сау по задающему и возмущающему воздействиям.
- •3.Определить передаточные функции сау по входному сигналу g(t) и возмущению Мн(t).
- •3.1.Определить передаточную функцию по входу от задающего воздействия при равенстве нулю возмущающего воздействия при нулевых начальных условиях.
- •3.2.Определить передаточную функцию по входу от возмущающего воздействия при равном нулю задающего воздействия при нулевых начальных условиях.
- •3.3. Определить передаточную функцию по входу от возмущающего воздействия при неравенстве 0 g(t) и при нулевых начальных условиях, когда канал компенсации замкнут.
- •4.Определить временные характеристики.
- •4.2.Рассчитать и построить переходную функцию.
- •4.3. Рассчитать функцию веса.
- •5.Частотные характеристики (рассчитать и построить).
- •5.2.Амплитудно-частотную характеристику
- •5.3.Фазочастотную характеристику
- •5.4.Логорифмитическая амплитудно-частотная характеристика
2. Составить дифференциальное уравнение сау по задающему и возмущающему воздействиям.
Дифференциальное ур-е САУ по задающему воздействию :
где, МН(t)=0 => Мн(s)* W2*W7*W8 = 0 ,
следовательно
Y(s)=
G(s)* W3*W4*W5*W6*W7*W8
= G(s) *
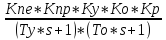 ,
,
тогда
(Ту*s+1)*(To*s+1)*Y(s)=G(s)*Кпе*Кпр*Ку*Ко*Кр
(Ту*То*s2 + (Ty+To)*s + 1)*Y(s) =G(s)*Кпе*Кпр*Ку*Ко*Кр
Ту*То*Y(s)*s2 + (Ty+To)*Y(s)*s + Y(s) = G(s)*Кпе*Кпр*Ку*Ко*Кр
Учитывая,
что S
=
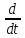 , имеем обратное преобразование
, имеем обратное преобразование
Ту*То*у``(t) + (Ty+To)*y`(t) + y(t) = g(t)*Кпе*Кпр*Ку*Ко*Кр
Подставив значения, получим:
0,04*y``(t) + 0,5*y`(t) + y(t) = 3,9*g(t)
Дифференциальное ур-е САУ по возмущающему воздействию:
где, g(t)=0 => G(s)* W3*W4*W5*W6*W7*W8 = 0
следовательно
Y(s)
=- Мн(s)*
W2*W7*W8
= -MH(s)
*

тогда
То*Y(s)*s +Y(s) = -MH(s)*Bo*Kp
или
0,4*y`(t) + y(t) = -0,5* MH(t)
3.Определить передаточные функции сау по входному сигналу g(t) и возмущению Мн(t).
3.1.Определить передаточную функцию по входу от задающего воздействия при равенстве нулю возмущающего воздействия при нулевых начальных условиях.
По условию МН(t)=0
тогда
Y(s)= G(s)* W3*W4*W5*W6*W7*W8
и
передаточная функция по входу от задающего воздействия:
WЗ(s)
=
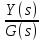 = W3*W4*W5*W6*W7*W8
=
= W3*W4*W5*W6*W7*W8
=
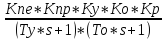 =
=
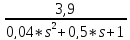
3.2.Определить передаточную функцию по входу от возмущающего воздействия при равном нулю задающего воздействия при нулевых начальных условиях.
По условию g(t)=0,
тогда
Y(s)= -Мн(s)* W2*W7*W8
и передаточная функция по входу от возмущающего воздействия:
Wвозм
=
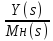 =
=
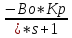 =
=
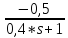
3.3. Определить передаточную функцию по входу от возмущающего воздействия при неравенстве 0 g(t) и при нулевых начальных условиях, когда канал компенсации замкнут.
Рассмотрим схему, когда канал компенсации замкнут:
W2
W4*W5*W6




W1
МН(s)
A D_
W7*W8
W3
G(s)
B C
Y(s)

-
Передаточная функция, когда g(t)=const, Мн(t)=0 и канал разомкнут:
Описано в п.п. 3.1.
-
Передаточная функция, когда g(t)=0, Мн(t)=const и канал разомкнут:
Описано в п.п. 3.2.
-
Передаточная функция, когда g(t)=const, Мн(t)=const и канал разомкнут:
Y(s)=
G(s)* W3*W4*W5*W6*W7*W8
- Мн(s)*
W2*W7*W8
=
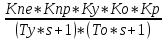 * G(s) -
* G(s) -
 *
Мн(s)
=
*
Мн(s)
=
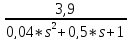 *
G(s)
*
G(s)
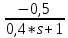 *
Мн(s)
*
Мн(s)
-
Передаточная функция, когда g(t)=const, Мн(t)=const и канал замкнут:
Y(s) = G(s)* W3*W4*W5*W6*W7*W8 + МН(s)*W1* W4*W5*W6*W7*W8 - МН(s)* W2*W7*W8
=
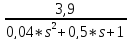 *
G(s) +
*
G(s) +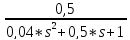 *
Мн(s)
*
Мн(s)
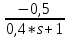 *
Мн(s)
*
Мн(s)
4.Определить временные характеристики.
4.1.Рассмотреть САУ при МH(t)=0, а входное воздействие G(t)=1(t) – скачок, y(0)=0, а первая производная y'(0)=0.
Y(s)=
G(s)* W3*W4*W5*W6*W7*W8
= G(s) *
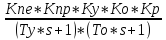
(Ту*s+1)*(To*s+1)*Y(s)=G(s)*Кпе*Кпр*Ку*Ко*Кр
(Ту*То*s2 + (Ty+To)*s + 1)*Y(s) =G(s)*Кпе*Кпр*Ку*Ко*Кр
Ту*То*Y(s)*s2 + (Ty+To)*Y(s)*s + Y(s) = G(s)*Кпе*Кпр*Ку*Ко*Кр
Учитывая,
что S
=
 , имеем обратное преобразование
, имеем обратное преобразование
Ту*То*у``(t) + (Ty+To)*y`(t) + y(t) = g(t)*Кпе*Кпр*Ку*Ко*Кр
Подставив значения, получим:
0,04*y``(t) + 0,5*y`(t) + y(t) = 3,9*g(t)
4.2.Рассчитать и построить переходную функцию.
Исходя из условия п.п. 4.1. МН(t)=0 и g(t)=1(t) , и нулевые начальные условия, то рассмотрим дифференциальное ур-е САУ по задающему воздействию:
0,04*y``(t) + 0,5*y`(t) + y(t) = 3,9*g(t)
Учитывая,
что S
=
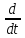 , а y(t)
, а y(t)
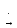 Y(s)
, g(t)
Y(s)
, g(t)
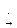 G(s)
, то
G(s)
, то
0,04*Y(s)*s2
+ 0,5*Y(s)*s
+ Y(s)
= 3,9*G(s)
, т.к. g(t)=1(t),
а изображение 1(t)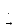
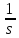 и учитывая, что при этом на Y(s)
накладывается обязательство быть
изображением переходной функции,
запишем:
и учитывая, что при этом на Y(s)
накладывается обязательство быть
изображением переходной функции,
запишем:
0,04*H(s)*s2
+ 0,5*H(s)*s + H(s) = 3,9*
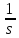 => H(s) =
=> H(s) =
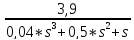
Для того, чтоб узнать переходную функцию, воспользуемся формулой разложения Карсона – Хевисайда:
h(t)
=
 ,
,
где
С(s) = 3,9
D`(s)
= ( )`
= 0,12*s2
+ s
+ 1
)`
= 0,12*s2
+ s
+ 1
Найдем корни хар-ого уравнения:
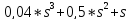 =
0
=
0
s1=0 ,
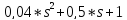 =
0
=
0
s2=
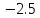 ; s3
= -10
; s3
= -10
тогда за формулою разложения Хевисайда:
h(t)
=
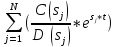 =
=
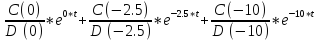
h(t) = 1.3*e-10.0*t-5.2*e-2.5*t+3.9
|
t |
h(t) |
|
0 |
0 |
|
1 |
3.473 |
|
2 |
3.865 |
|
3 |
3.897 |
|
6 |
3.9 |
|
10 |
3.9 |
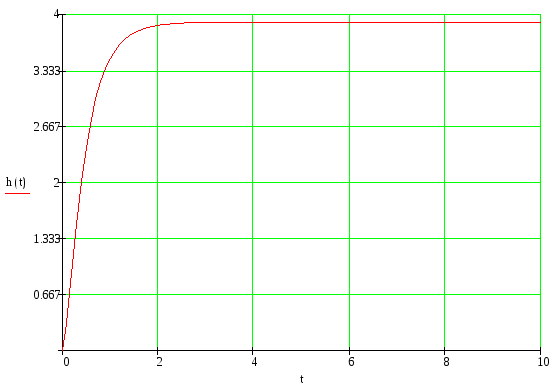
График переходной функции
