Рассмотрим две прямые
L1:
L2
:
,
если прямая
L1
параллельна
L2
, то
выполняется условие :
(4)
5.) Условие перпендикулярности прямых
l 1 l2 + m1 m 2 +n1 n2 =0 (5)
6). Общее уравнение плоскости
Ax + By + Cz+D = 0 , (6)
где A, B, C, D – координаты вектора нормали, причем хотя бы одно из чисел A, B, С отлично от нуля, (x;y;z) - координаты любой точки на плоскости. Геометрический смысл коэффициентов А, В, С в уравнении (1) – это проекции вектора, перпендикулярного плоскости.
7.) Уравнение плоскости, проходящей через три точки
M0 (x0,y0,z0), M1 (x1,y1,z1), M2 (x2,y2,z2)
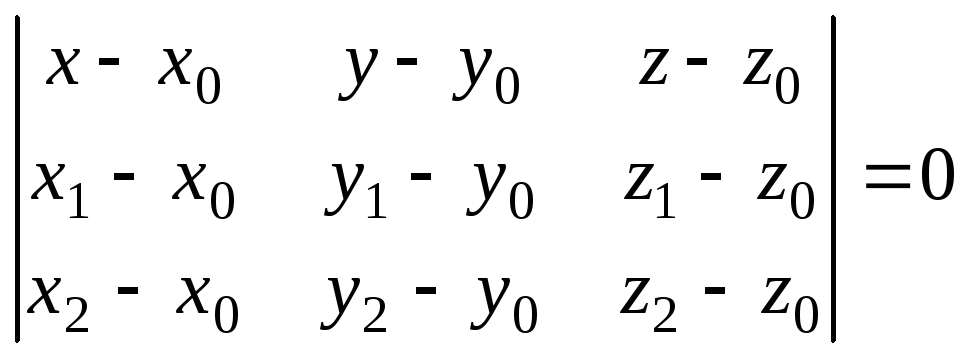(7)
или
(x-x0) ((y1-y0)(z2-z0)-(y2-y0)(z1-z0)) – (y-y0) ((x1-x0)(z2-z0)-(x2-x0)(z1-z0))+
+(z-z0) ((x1-x0)(y2-y0)-(x2-x0)(y1-y0))=0
8). Условие параллельности плоскостей
Рассмотрим две плоскости
Р1: A1 x+B1 y+C1 z+D1=0
Р2:A2x+B2y+C2z+D2=0, если плоскость Р1 параллельна Р2, то выполняется условие :
(8)
9.) Условие перпендикулярности плоскостей
A1 A2 + B1B 2 + C1 С2 =0 (9)
10.а) угол между плоскостями
A1 x+B1 y+C1 z+D1=0 и A2 x+B2 y+C2 z+D2=0
(10.а)
10.б) угол между векторами
и
(10.б)
10.в) угол между прямой и плоскостью
прямая L с направляющими коэффициентами (l, m, n) и плоскость Ax+By+Cz+D=0
(10.в)
11.) Расстояние между двумя точками
Даны точки А1 (x1,y1,z1) и А2 (x2,y2,z2), расстояние между ними:
(11)
12.) Расстояние от точки M0 (x0,y0,z0) до плоскости
A x+B y+C z+D=0 :
(12)
13.)
Выражение
векторного произведения через координаты
сомножителей
, если
,
,
то
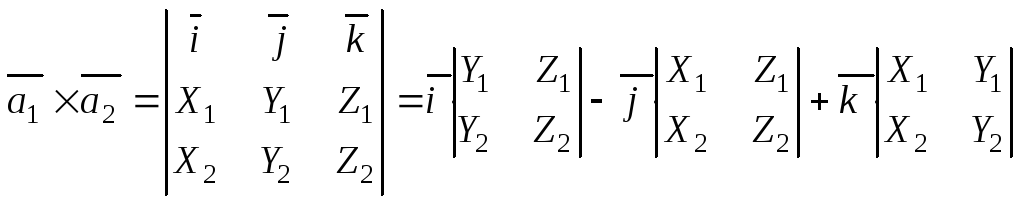(13)
Первая строка определителя состоит из координатных ортов, вторая из проекций первого сомножителя, третья из проекций второго сомножителя.
14.) Объем параллелепипеда, построенного на векторах
,
,
(14)
знак выбирается таким образом, чтобы объем был положительный.
Рассмотрим несколько примеров применения приведенных формул.
Задача 3.
Даны точки А 1 (1,-1,-2), А 2 (2,1,0), А 3 (-1,0,2), А 4 (0,1,1) .
3.а.) Найти длину ребра А1 А2.
Воспользуемся формулой (11). Расстояние между двумя точками.
Длина ребра А1 А2 равна 3 .
3.б.) Составить уравнение ребра А1 А4 .и грани А1А2А3.
Составим уравнение прямой проходящей через точки
А 1 (1,-1,-2) и А 4 (0,1,1), воспользуемся формулой (2)
;
Найдем уравнение плоскости, проходящей через точки
А 1 (1,-1,-2), А 2 (2,1,0), А 3 (-1,0,2),
Воспользуемся формулой (7)
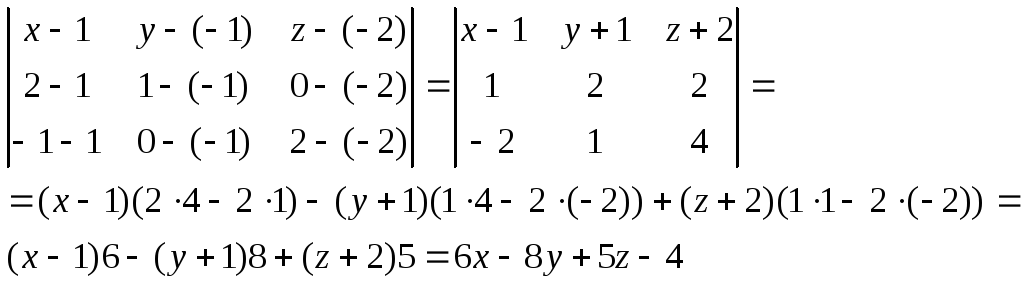
уравнение
грани 6x-8y+5z-4=0,
ребра
3.в) Составить уравнение высоты опущенной из точки
А 4 (0,1,1) на плоскость А1А2А3.
Высота
проходит через точку А
4
(0,1,1) и
перпендикулярна
плоскости 6x-8y+5z-4=0,
имеющей вектор нормали
.
Направляющий
вектор высоты совпадает с вектором
нормали данной плоскости, следовательно
т.к.
(2) , то
уравнение искомой высоты.
или в параметрической форме (3)
x=6t, y=1-8t, z=1+5t
3.г.) Найти площадь треугольника А1A2A3 с вершинами
А 1 (1,-1,-2), А 2 (2,1,0), А 3 (-1,0,2),
Площадь
треугольника будет равна 1/2
площади параллелограмма, построенного
на векторах
и
.
Площадь параллелограмма равна модулю
векторного произведения этих векторов.
Воспользуемся формулой (13)
;
,
3.д) Найти объем треугольной пирамиды А1A2А3A4 с вершинами
А 1 (1,-1,-2), А 2 (2,1,0), А 3 (-1,0,2), А 4 (0,1,1) .
Искомый объем равен 1/6 объема параллелепипеда, построенного на ребрах А1A2, А1A3, А1A4. Воспользуемся формулой (14)
,
,
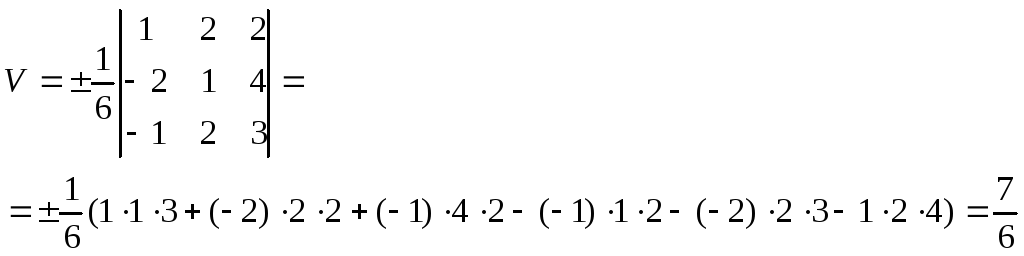
Задача 4.
4.1-4.20. Найти собственные числа и собственные векторы матрицы А.
4.1.
А
=
;
4.2. А
=
;
4.
3. А
=
;
4.4. А
=
;
4.
5. А
=
;
4.6. А
=
;
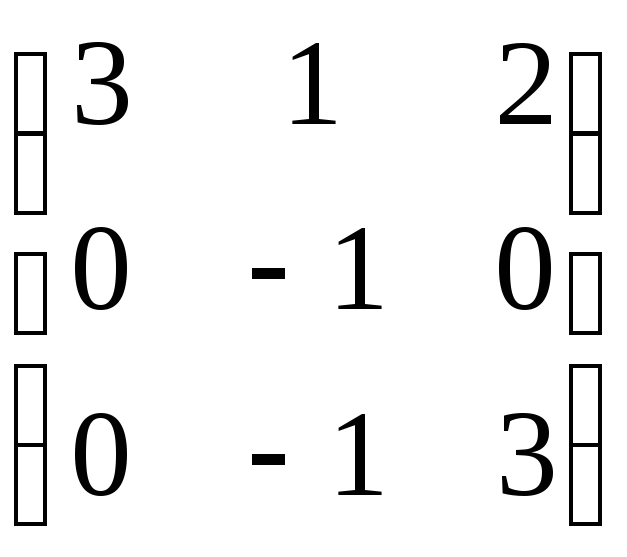4.7.
А
=
;
4.8. А
=
;
4.9.
А
=
;
4.10. А
=
;
4.
11. А
=
;
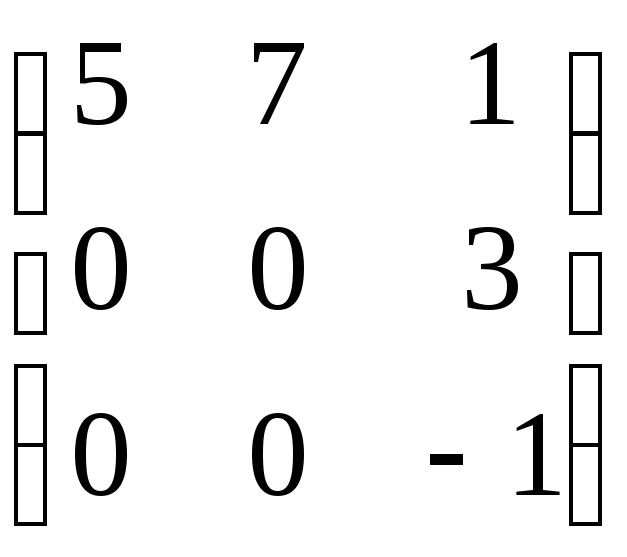4.12. А
=
;
4.13.
А
=
;
4.14. А
=
;
4.15.
А
=
;
4.16. А
=
;
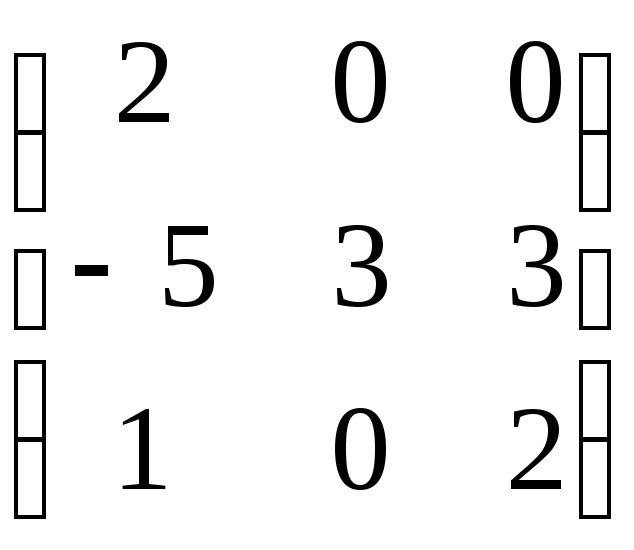4.17.
А
=
;
4.18. А
=
;
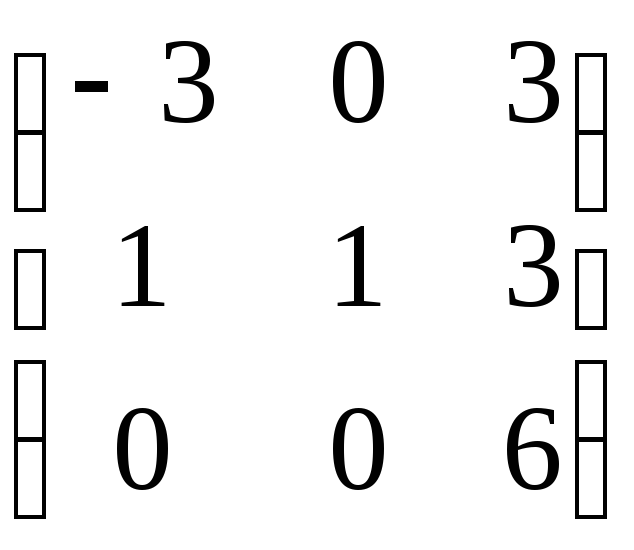4.19.
А
=
;
4.20. А
=
.
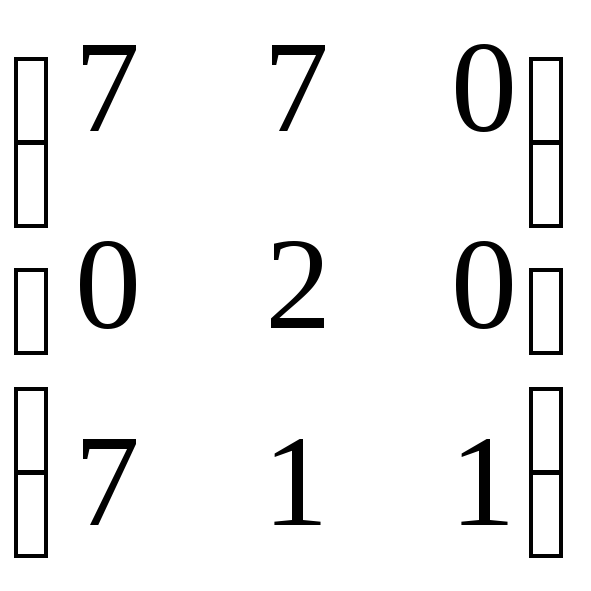Указания к задаче 4: собственные числа и собственные векторы
Число
называется собственным
числом
квадратной матрицы А
n-ого
порядка, если существует такой ненулевой
n-мерный
вектор Х,
что АХ=
Х.
Этот
ненулевой вектор Х
называется собственным
вектором
матрицы А,
соответствующим ее собственному числу
.
Множество
всех собственных чисел матрицы А
совпадает с множеством всех решений
уравнения
,
которое называется характеристическим
уравнением матрицы А.
Множество
всех собственных векторов матрицы А,
соответствующих ее собственному числу
,
совпадает с множеством всех ненулевых
решений системы однородных уравнений
(А
-
Е)
= 0.
Задача 4.
Найти собственные числа и собственные векторы матрицы А.
А
=
.
Решение:
Найдем характеристическое уравнение
матрицы А
– определитель матрицы А
-
Е,
где Е
– единичная матрица,
–независимая переменная.
А
–
Е
=
–
=
.
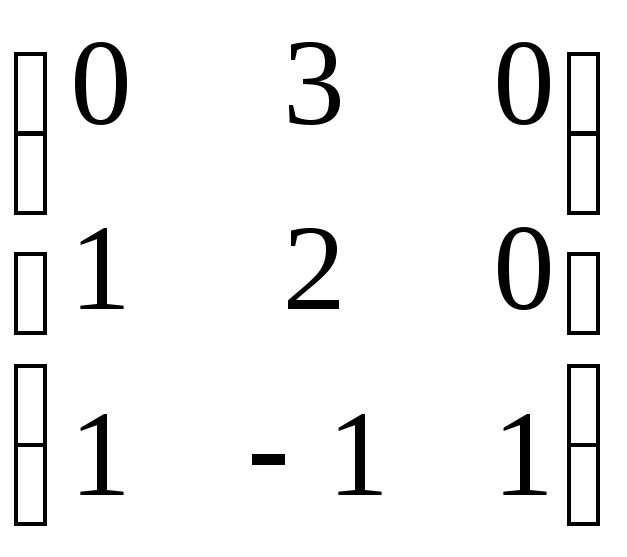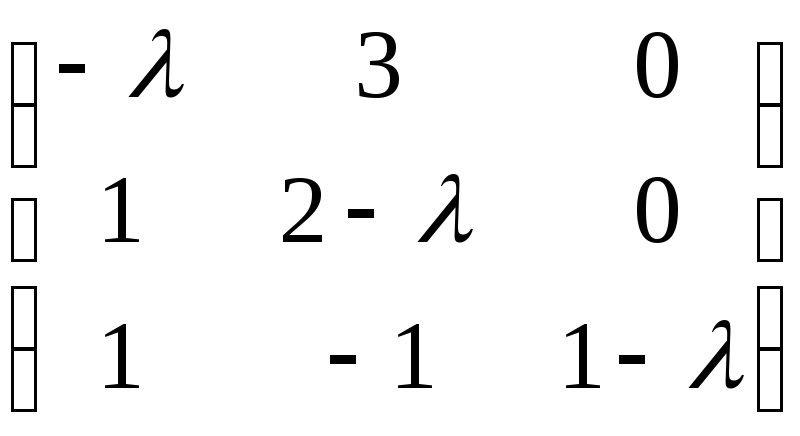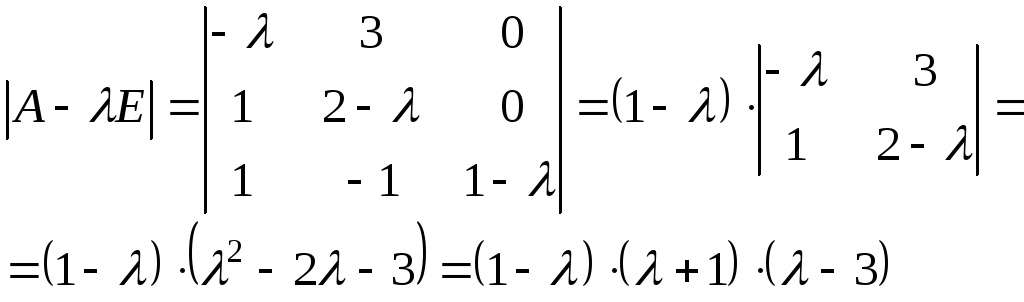
При вычислении данного определителя использовалось его разложение по элементам третьего столбца.
Найдем
теперь собственные числа матрицы А
– корни характеристического уравнения
.
Получаем:
,
,
.
Далее найдем собственные векторы матрицы А, соответствующие каждому из собственных чисел.
Пусть
Х
=
– искомый собственный вектор.
Тогда
система однородных уравнений (А
-
Е)
= 0
выглядит так:
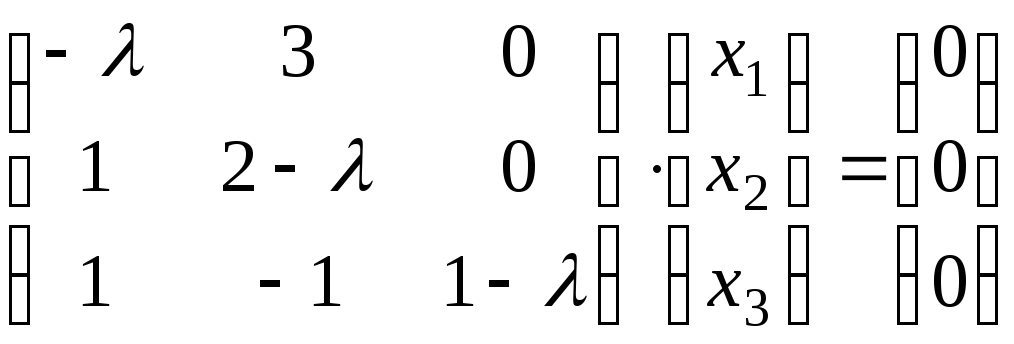
или
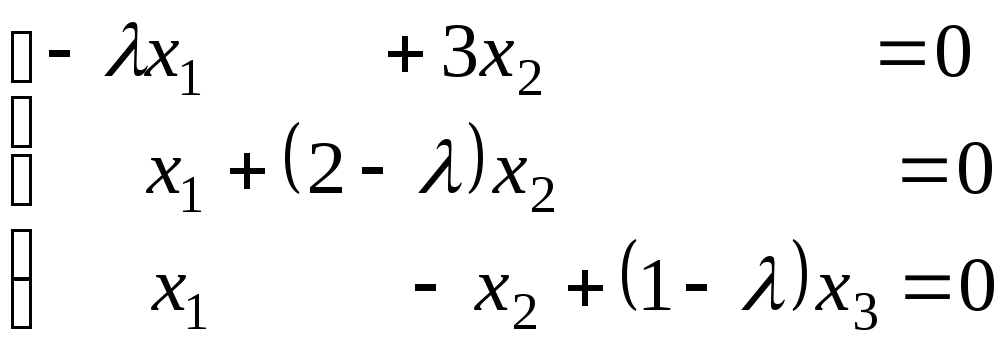(1)
Эта однородная система линейных уравнений имеет множество решений, так как ее определитель равен нулю.
При
система (1) принимает вид:
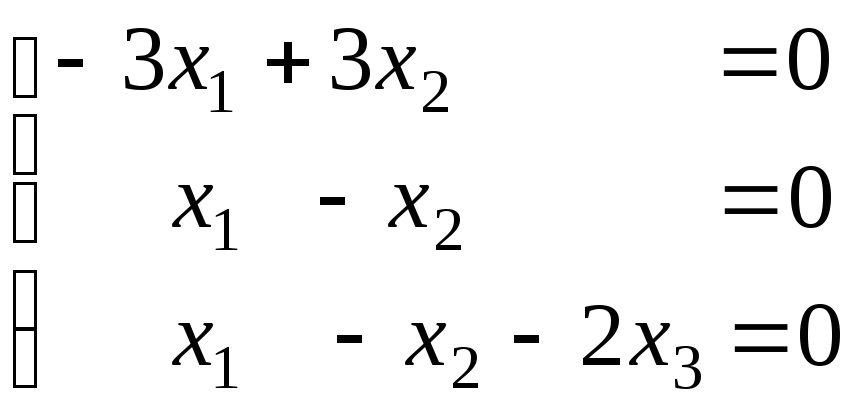
Общее
решение этой системы
,
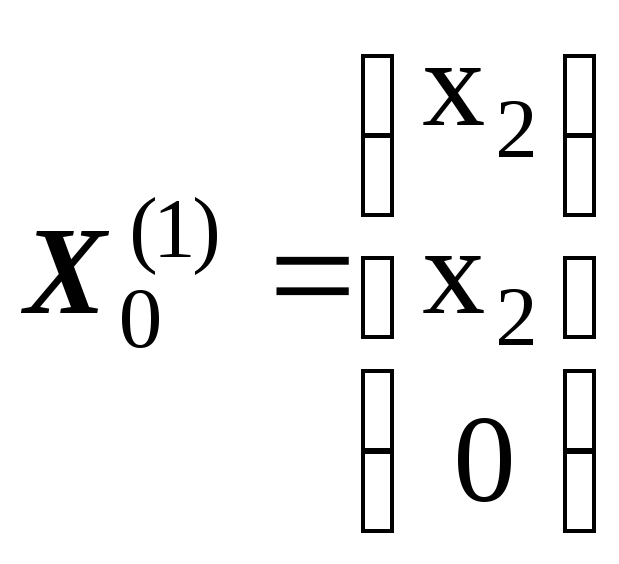где
любое число.
В
качестве собственного вектора достаточно
взять любое частное решение. Пусть,
например,
,
тогда собственный вектор, соответствующий
собственному числу
,
имеет вид
.
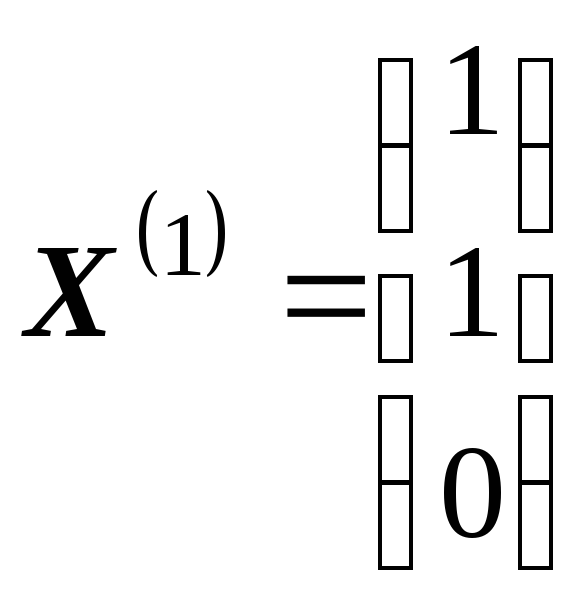При
система (1) принимает вид:
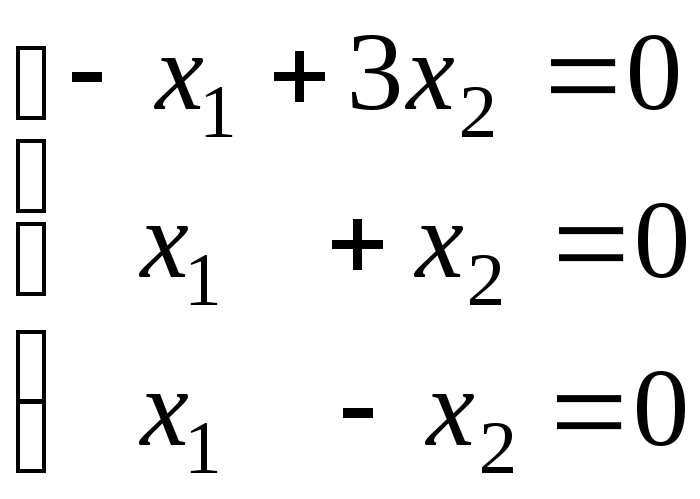
Общее
решение этой системы
,
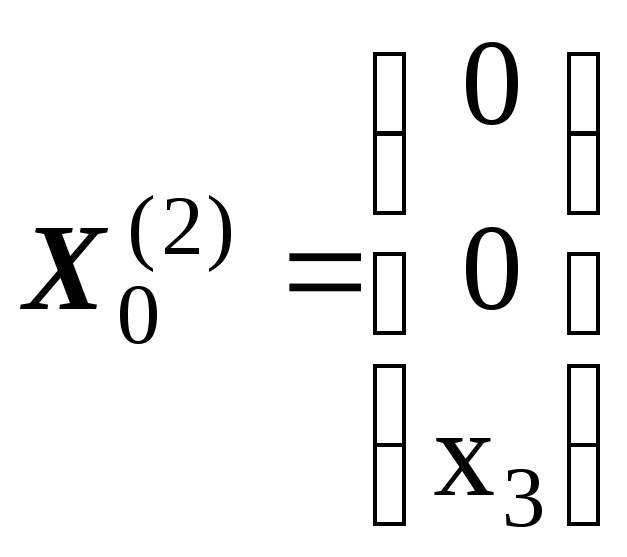где
любое число.
Пусть,
например,
,
тогда собственный вектор, соответствующий
собственному числу
,
имеет вид
.
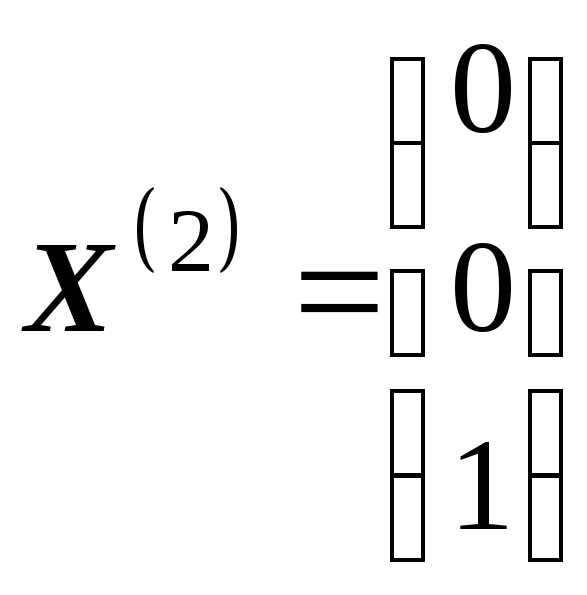Аналогично
при
получаем систему
,
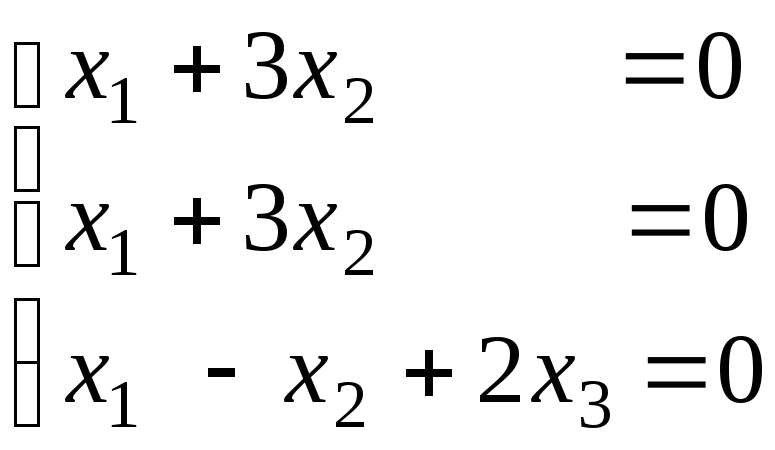общее
решение которой
,
где
любое число.
Пусть
,
тогда собственный вектор, соответствующий
собственному числу
,
имеет вид
.
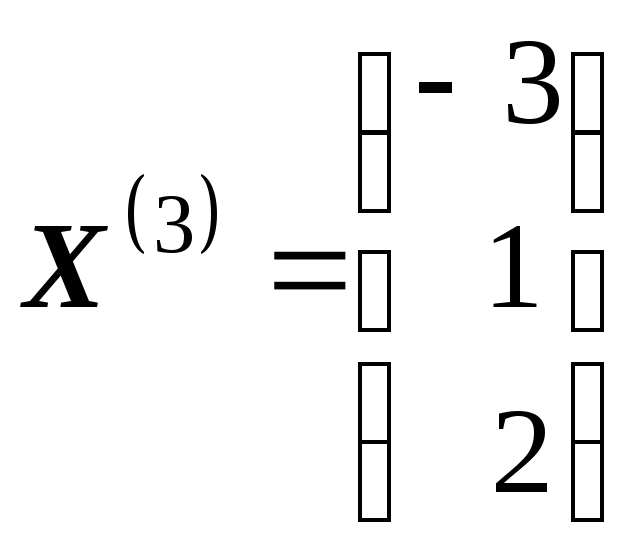Ответ:
,
,
,
,
,
.
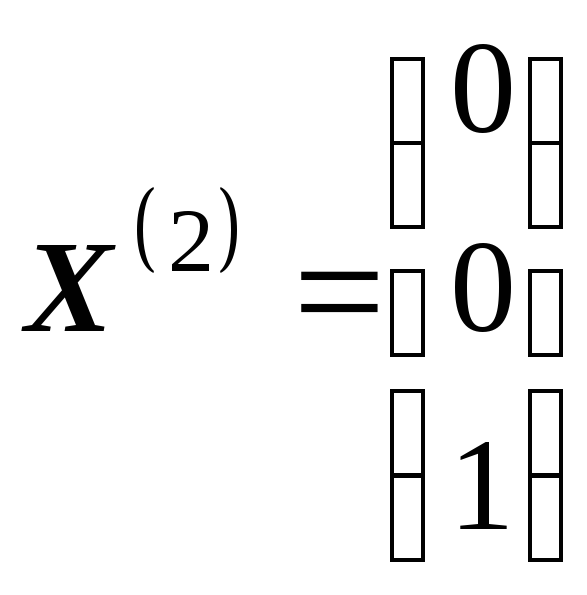
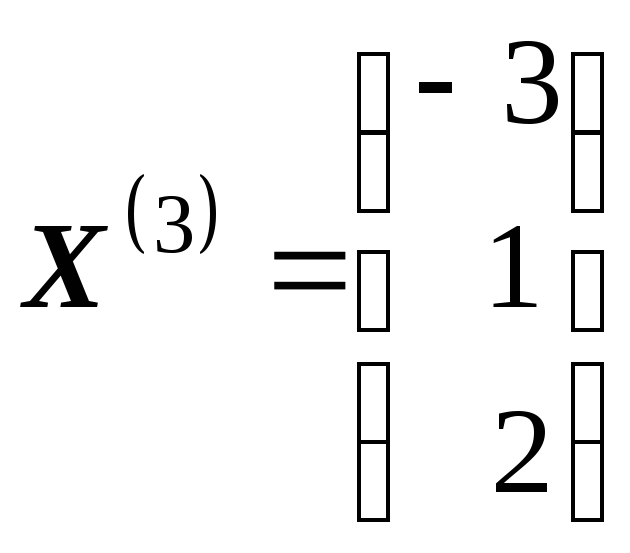